整除
设 $n$ 为非负整数,$d$ 为正整数,若 $\frac{n}{d}$ 为整数,则称 $d$ 整除 $n$,记为 $d \mid n$,称 $d$ 为 $n$ 的约数,或因数,或因子,而称 $n$ 为 $d$ 的倍数。
任何正整数都整除 $0$。
$d$ 不整除 $n$ 记为 $d \nmid n$。
最大公约数
设 $a, b$ 为非负整数,$d$ 为正整数,若 $d \mid a$ 且 $d \mid b$,则称 $d$ 为 $a$ 和 $b$ 的公约数,或公因数,或公因子。
$a$ 和 $b$ 的所有公约数中最大的数称为 $a$ 和 $b$ 的最大公约数,或最大公因数,或最大公因子,记为 $\gcd(a, b)$,有时简记为 $(a, b)$。
根据定义,显然有 $gcd(a, b) = gcd(b, a)$。
若 $gcd(a, b) = 1$,则称 $a$ 和 $b$ 互质或互素。
由于任何正整数都是 $0$ 和 $0$ 的公约数,故 $gcd(0, 0)$ 不存在。
对任意正整数 $a$,有 $gcd(0, a) = a$。
gcd 的性质
设 $a, b$ 为正整数且 $a > b$,有性质
$$gcd(b, a) = gcd(b, a - b)$$
由此可进一步得到性质
$$gcd(b, a) = gcd(b, a \, mod \, b)$$
对于斐波那契数列的 $\color{red}{\gcd}$ 有个特殊性质:
$$ \gcd(fib[a], fib[b]) = fib[\gcd(a, b)] $$
gcd 的计算
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
复杂度为 $O(\log \max(a, b))$
例题
给出数列 $A$,询问 $[l, r]$ 的 $\gcd$
最小公倍数
设 $a, b$ 为正整数,$m$ 为非负整数,若 $a \mid m$ 且 $b \mid m$,则称 $m$ 为 $a$ 和 $b$ 的公倍数。
$a$ 和 $b$ 的所有公倍数中最小的正数称为 $a$ 和 $b$ 的最小公倍数,记为 $lcm(a, b)$。
根据定义,显然有 $lcm(a, b) = lcm(b, a)$。
一个显然而重要的公式是
$$lcm(a, b) = \frac{ab}{gcd(a, b)}$$
这个公式给出了 $lcm$ 与 $gcd$ 的关系。
需要注意的是,在实际的代码实现中,为避免中间结果的溢出,应该使用 $a / gcd(a, b) * b$ 而不是 $a * b / gcd(a, b)$。
质数
设 $n \geqslant 2$ 为整数,若所有满足 $1 < k < n$ 的整数 $k$ 都不是 $n$ 的约数,则称 $n$ 为质数或素数,否则称 $n$ 为合数。
$1$ 既不是质数,也不是合数。
质数个数
定义 $\pi(n)$ 为不大于 $n$ 的质数个数,可以证明
$$\pi(n) = O(\frac{n}{\log n})$$
唯一分解定理
设 $n \geqslant 2$ 为整数,则有唯一的分解式
$$n = \prod\limits_{i = 1}^m {p_i^{{k_i}}}$$
其中 $p_1 < p_2 < \cdots < p_m$ 为质数,$k_i$ 为正整数。
可以证明 $m = O(\log \log n)$。
质因数分解
分解方法一
vector<int> factor(int n) {
vector<int> f;
for (int i = 2; i <= n; ++i) {
while (n % i == 0) {
f.push_back(i);
n /= i;
}
}
return f;
}
分解方法二
vector<int> factor(int n) {
vector<int> f;
for (int i = 2; i * i <= n; ++i) {
while (n % i == 0) {
f.push_back(i);
n /= i;
}
}
if (n > 1) f.push_back(n);
return f;
}
分解方法三
vector<int> p; // 质数表
vector<int> factor(int n) {
vector<int> f;
for (int i = 0; i < p.size(); ++i) {
if (p[i] * p[i] > n) break;
while (n % p[i] == 0) {
f.push_back(p[i]);
n /= p[i];
}
}
if (n > 1) f.push_back(n);
return f;
}
复杂度分析
- 方法一的复杂度为 $O(n)$
- 方法二的复杂度为 $O(\sqrt{n})$
- 方法三的复杂度为 $O(\frac{\sqrt{n}}{\log n})$
筛法
求所有不大于 n 的质数
容易想到对所有不大于 $n$ 的正整数逐个判断是不是质数,但这不是好主意。
调和级数
设调和级数前 $n$ 项的和为 $f(n)$,即
$$f\left( n \right) = \sum\limits_{i = 1}^n {\frac{1}{i}}$$
可以证明
$$f(n) = O(\log n)$$
筛法一
从 $2$ 到 $n$ 枚举整数 $i$,标记大于 $i$ 且不大于 $n$ 的 $i$ 的倍数。枚举到 $i$ 时,若 $i$ 没有被标记过,则 $i$ 为质数。
复杂度为
$$O\left( {\sum\limits_{i = 1}^n {\frac{n}{i}} } \right) = O\left( {n\log n} \right)$$
bool vis[N + 1];
vector<int> p;
void sieve() {
for (int i = 2; i <= N; ++i) {
if (!vis[i]) p.push_back(i);
for (int j = i * 2; j <= N; j += i)
vis[j] = 1;
}
}
筛法二
从 $2$ 到 $n$ 枚举整数 $i$,若 $i$ 是质数,标记大于 $i$ 且不大于 $n$ 的 $i$ 的倍数。枚举到 $i$ 时,若 $i$ 没有被标记过,则 $i$ 为质数。
可以证明复杂度为 $O(n\log \log n)$。这种筛法有个不好记的名字。
bool vis[N + 1];
vector<int> p;
void sieve() {
for (int i = 2; i <= N; ++i) {
if (!vis[i]) {
p.push_back(i);
for (int j = i * 2; j <= N; j += i)
vis[j] = 1;
}
}
}
筛法三
从 $2$ 到 $n$ 枚举整数 $i$,再从小到大枚举所有不大于 $i$ 的最小质因子 $p_0$,标记为 $ip_0$。显然,枚举到的 $p_0$ 总是 $ip_0$ 的最小质因子,而更大的 $p_0$ 均不可能是 $ip_0$ 的最小质因子。同样,枚举到 $i$ 时,若 $i$ 没有被标记过,则 $i$ 为质数。
每个合数都只会在其最小的质因子被枚举时被标记,故复杂度为 $O(n)$,这种筛法称为欧拉筛或线性筛。
bool vis[N + 1];
vector<int> p;
void sieve() {
for (int i = 2; i <= N; ++i) {
if (!vis[i]) p.push_back(i);
for (int j = 0; i * p[j] <= N; ++j) {
vis[i * p[j]] = 1;
if (i % p[j] == 0) break;
}
}
}
例题1:素数个数
Code:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
const int N = 100000005;
// linear sieve
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void sieve(int n) {
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n/i; j ++ ) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int main() {
int n;
cin >> n;
sieve(n);
cout << cnt << '\n';
return 0;
}
例题2:素数密度
${\rm Eratosthenes}$ 区间筛
Code:
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::vector;
using ll = long long;
int main() {
ll l, r;
cin >> l >> r;
vector<bool> isprime(50000, true);
vector<bool> isprime2(r-l+1, true);
// 筛
for (ll p = 2; p*p <= r; ++p) {
// 已经是合数的跳过
if (!isprime[p]) continue;
// 从除 p 以外的 p 的倍数中去掉他们的素数标签
for (ll q = p*2; q*q <= r; q += p) {
isprime[q] = false;
}
// start: 大于等于 A 的最小的 p 的倍数
ll start = (l + p - 1) / p * p;
if (start == p) start = p*2;
// 筛掉在 A 与 B 之间的 p 的倍数
for (ll q = start; q <= r; q += p) {
isprime2[q-l] = false;
}
}
ll ans = 0;
for (ll q = l; q <= r; ++q) {
if (q == 1) continue;
if (isprime2[q-l]) ++ans;
}
cout << ans << '\n';
return 0;
}
整除分块(数论分块)
看一个有趣的小问题,求
$$ \sum_{i=1}^n\lfloor \frac{n}{i} \rfloor $$
其中 $n \leqslant 10^{12}$
那么暴力 $O(n)$ 做肯定不行
先打个表找找规律,假设 $n = 10$,可以发现,结果的个数不是很多,而且总有一大块数字是一样大小的。这样一块一块分布的数字,叫做整除分块。
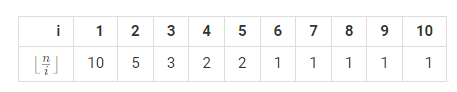
整除分块的性质
性质 $1$:$\lfloor \frac{n}{i} \rfloor$ 最多只有 $2\sqrt{n}$ 种取值
证明:对于 $i \leqslant \sqrt{n}$,最多只有 $\sqrt{n}$ 种取值。而对于 $i > \sqrt{n}$,有 $\frac{n}{i} < \sqrt{n}$,也最多只有 $\sqrt{n}$ 种取值,所以总的值最多不超过 $2\sqrt{n}$ 种。
性质 $2$:若 $\lfloor\frac{n}{r}\rfloor$ 与 $\lfloor\frac{n}{i}\rfloor$ 相等,那么 $r$ 的最大取值为 $\lfloor\frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor$
证明:设 $\lfloor \frac{n}{i} \rfloor = k$,于是如果 $r$ 取到比较大的数字,使得 $\lfloor \frac{n}{r} \rfloor$ 与 $\lfloor \frac{n}{i} \rfloor$不相等,那么 $\lfloor \frac{n}{r} \rfloor < k$,也即 $\frac{n}{r} < k$,也即 $r > \frac{n}{k}$,那么 $r > \lfloor \frac{n}{k} \rfloor$,即 $r > \lfloor\frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor$,所以 $r$ 最大取到 $\lfloor\frac{n}{\lfloor \frac{n}{i} \rfloor}\rfloor$ 可以使得 $\lfloor\frac{n}{r}\rfloor$ 与 $\lfloor\frac{n}{i}\rfloor$ 相等
有了上面两条性质,我们就可以定义两个变量 $l$ 和 $r$,每次计算一个相等的区间 $[l, r]$ 的值,乘以区间长度,然后计算下一个区间。区间个数是 $2\sqrt{n}$ 个,所以总复杂度是 $O(\sqrt{n})$
模板代码:
for (int l = 1, r; l <= n; l = r+1) {
r = n/(n/l);
ans += (r-l+1) * (n/l);
}
例题: 余数之和
给定正整数 $n$ 和 $k$,请计算
$$ G(n, k) = \sum_{i=1}^n k \% i $$
分析:
首先,我们知道 $$k \% i = k - i \times \lfloor \frac{k}{i} \rfloor$$
所以
$$ \sum_{i=1}^n k \% i = \sum_{i=1}^n (k - i \times \lfloor \frac{k}{i} \rfloor) = \sum_{i=1}^n k - \sum_{i=1}^n i \times \lfloor \frac{k}{i} \rfloor= nk - \sum_{i=1}^n i \times \lfloor \frac{k}{i} \rfloor $$
而 $\sum\limits_{i=1}^n i \times \lfloor \frac{k}{i} \rfloor$ 可以用整除分块来求,每次求一个 $\lfloor \frac{k}{i} \rfloor$ 值固定的区间 $[l, r]$,这时候把 $\lfloor \frac{k}{i} \rfloor$ 提出来,剩下部分是一个等差数列,直接用公式求和,再乘以 $\lfloor \frac{k}{i} \rfloor$ 即可
代码实现
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::min;
using ll = long long;
int main() {
ll n, k;
cin >> n >> k;
ll ans = n*k;
for (ll l = 1, r; l <= n; l = r+1) {
ll t = k/l;
if (t == 0) break;
r = min(k/t, n);
ans -= t * (l+r)*(r-l+1)/2;
}
cout << ans << '\n';
return 0;
}
积性函数
设 $f(n)$ 为定义在正整数上的函数,如果 $f(1) = 1$,且对于任意正整数 $a, b$,只要 $a$ 和 $b$ 互质,就有
$$f(ab) = f(a)f(b)$$
则称 $f(n)$ 为积性函数。
如果不要求 $a$ 和 $b$ 互质,则称 $f(n)$ 为完全积性函数。
计算方法
一般地,求出 $n$ 的分解式 $n = \prod\limits_{i = 1}^k {p_i^{{k_i}}}$,则有
$$f\left( n \right) = \prod\limits_{i = 1}^k {f\left( {p_i^{{k_i}}} \right)}$$
求 $f(p_i^{k_i})$ 的方法依赖于具体的 $f$ 的性质,没有一般性的方法。
在线性筛过程中计算积性函数
bool vis[N + 1];
vector<int> p;
int c[N + 1], f[N + 1];
void sieve() {
for (int i = 2; i <= N; ++i) {
if (!vis[i]) {
p.push_back(i);
for (int j = i, k = 1;; ++k) {
c[j] = j;
f[j] = cal(i, k);
if (j > N / i) break;
j *= i;
}
}
for (int j = 0; i * p[j] <= N; ++j) {
vis[i * p[j]] = 1;
if (i % p[j] == 0) {
c[i * p[j]] = c[i] * p[j];
f[i * p[j]] = f[i / c[i]] * f[c[i] * p[j]];
break;
}
c[i * p[j]] = p[j];
f[i * p[j]] = f[i] * f[p[j]];
}
}
}
积性函数举例
约数函数
定义 $\sigma_x(n)$ 为 $n$ 的所有约数的 $x$ 次方和,即
$$\sigma_x\left( n \right) = \sum_{\left. d \right|n} {d^x}$$
特别地,$\sigma_0(n)$ 为 $n$ 的约数个数,常记为 $d(n)$ 或 $\tau(n)$;$\sigma_1(n)$ 为 $n$ 的约数和,常简记为 $\sigma(n)$。
可以证明 $\sigma_x(n)$ 为积性函数。
对于质数 $p$ 和正整数 $k$,有
$$\sigma_x\left( {p^k} \right) = \sum_{i = 0}^k {{\left( {{p^i}} \right)}^x} = \sum_{i = 0}^k {{\left( {{p^x}} \right)}^i}$$
从而当 $x \neq 0$ 时,有
$${\sigma_x}\left( {{p^k}} \right) = \frac{{{{\left( {{p^x}} \right)}^{k + 1}} - 1}}{{{p^x} - 1}}$$
欧拉 $\varphi$ 函数
定义 $\varphi(n)$ 为不大于 $n$ 的正整数中与 $n$ 互质的数的个数,即
$$\varphi \left( n \right) = \sum\limits_{i = 1}^n {\left[ {\gcd \left( {i,n} \right) = 1} \right]}$$
其中 $[x]$ 在 $x$ 成立时为 $1$,否则为 $0$。
可以证明 $\varphi(n)$ 为积性函数。
对于质数 $p$ 和 正整数 $k$,有
$$\varphi \left( {{p^k}} \right) = {p^k} - {p^{k - 1}} = {p^{k - 1}}\left( {p - 1} \right)$$
模算术
取模
设 $a$ 为整数,$n$ 为正整数,定义
$$
a \, \bmod \, n = \begin{cases}
a - \lfloor \frac{a}{n} \rfloor n, & a \geqslant 0 \\\
-(-a \, \bmod \, n), & a < 0
\end{cases}
$$
这与 C++ 中的取模运算符的行为一致。
同余
若 $(a - b) \bmod n = 0$,则称 $a$ 和 $b$ 同余,记为
$$a \equiv b \pmod n$$
$a$ 和 $b$ 均为正数时,此式等价于 $a \bmod n = b \bmod n$。
基本运算
模算术的基本性质
设 $a_0 = a \bmod n$,$b_0 = b \bmod n$,有
$$a + b \equiv a_0 + b_0 \pmod n\\\
ab \equiv a_0 b_0 \pmod n$$
对任意正整数 $k$,有
$$a \bmod n = (a \bmod kn) \bmod n$$
若 $k \mid a$,有
$$\frac{a}{k} \bmod n = \frac{a \bmod kn}{k}$$
取模优化
template<class T>
inline T mod(T a) {
return a < p ? a : a - p;
}
用内嵌汇编实现模乘法
u32 mul(u32 a, u32 b) {
asm(
"mul %%ebx\n"
"div %%ecx"
: "=d"(a)
: "a"(a), "b"(b), "c"(p)
);
return a;
}
快速幂
int pow(int a, int n) {
int s = 1;
for(; n; n >>= 1) {
if (n & 1) s = (ll)s * a % p;
if (n > 1) a = (ll)a * a % p;
}
return s;
}
快速乘
u64 mul(u64 a, u64 b) {
u64 s = 0;
for(; b; b >>= 1) {
if (b & 1) s = mod(s + a);
if (b > 1) a = mod(a + a);
}
return s;
}
注记
快速幂有一个更直观的名字:平方求幂法。
类比这个名字,快速乘可以称为“加倍求积法”。毕竟,快速乘不仅完全不快,反而非常慢,称其为“快速”乘显得有些荒唐。
用内嵌汇编实现64位模乘法
u64 mul(u64 a, u64 b) {
asm(
"mulq %%rbx\n"
"divq %%rcx"
: "=d"(a)
: "a"(a), "b"(b), "c"(p)
);
return a;
}
用 long double 实现64位模乘法
u64 mul(u64 a, u64 b, u64 n) {
u64 q = (long double)a * b / n;
return (a * b - q * n + n) % n;
}
只要编译器支持 long double 且 $0 \leqslant a, b < n \leqslant 2^{63}$,理论上不会出错。
乘法逆元与幂
模乘法的逆元
设 $a$ 为整数,$n$ 为正整数,若整数 $b$ 满足
$$ab \bmod n = 1$$
则称 $b$ 为 $a$ 模 $n$ 的逆元,记为 $a^{-1}$ 或 $\frac{1}{a}$。
容易证明以下结论:
- 当且仅当 $\gcd(a, n) = 1$时,$a$ 模 $n$ 的逆元存在。
- 如果 $b_1, b_2$ 为 $a$ 模 $n$ 的逆元,则必有 $b_1 \equiv b_2 \pmod n$,即 $a$ 模 $n$ 的逆元在模 $n$ 意义下唯一。
费马小定理
设 $p$ 为质数,$a$ 为与 $p$ 互质的整数,则有
$$a^{p - 1} \equiv 1 \pmod p$$
由此可知
$$
\begin{aligned}
a \cdot a^{p-2} &\equiv 1 \\\
a^{-1} &\equiv a^{p-2} \pmod p
\end{aligned}
$$
从而可以用快速幂计算 $a$ 模 $p$ 的逆元。
预处理逆元
设 $p$ 为质数,$n$ 为小于 $p$ 的正整数,求 $[1, n]$ 中的每个整数模 $p$ 的逆元。
若对每个数分别求逆元,复杂度为 $O(n \log p)$。
注意到逆元是积性函数,可以用线性筛求,复杂度为 $O(\frac{n\log p}{\log n})$。
设 $i$ 为 $[1, n]$ 中的整数,有
$$p = \lfloor \frac{p}{i} \rfloor i + (p \bmod i)$$
从而有
$$\frac{1}{i} \equiv -\frac{\lfloor \frac{p}{i} \rfloor}{p \bmod i} \pmod p$$
由于 $p \bmod i < i$,可以 $O(n)$ 递推计算。
inv[1] = 1;
for (int i = 2; i <= n; ++i) {
inv[i] = (ll)(p - p / i) * inv[p % i] % p;
}
注意到 $\frac{1}{i!} = \frac{i + 1}{(i + 1)!}$,故只需要 $O(\log p)$ 算出 $\frac{1}{n!}$,之后就可以 $O(n)$ 递推计算所有 $\frac{1}{i!}$,从而算出 $\frac{1}{i}$。
// f是阶乘数组
// g是阶乘的逆元数组
// h是逆元数组
f[0] = 1;
for (int i = 1; i <= n; ++i)
f[i] = (ll)f[i - 1] * i % p;
g[n] = pow(f[n], p - 2);
for (int i = n - 1; i >= 0; --i)
g[i] = (ll)g[i + 1] * (i + 1) % p;
for (int i = 1; i <= n; ++i)
h[i] = (ll)g[i] * f[i - 1] % p;
欧拉定理
设 $n \geqslant 2$ 为整数,$a$ 为与 $n$ 互质的整数,则有
$$a^{\varphi(n)} \equiv 1 \pmod n$$
特别地,若 $n$ 为质数,有 $\varphi(n) = n - 1$,即得到费马小定理。
由此可知
$$a^{-1} \equiv a^{\varphi(n) - 1} \pmod n$$
由于计算 $\varphi(n)$ 的复杂度较高,一般不用这个公式计算 $a$ 模 $n$ 的逆元。
降幂公式
设 $n, k$ 为正整数,$a$ 为任意整数,总有
$$a^{k} \equiv a^{\min(k,k_0)} \pmod n$$
其中 $k_0 = (k \bmod \varphi(n)) + \varphi(n)$。
欧几里得算法
设 $a,b$ 为正整数且 $a < b$,则存在正整数数组 $q,r$,满足
$$
\begin{aligned}
a &= q_0b + r_0 \\\
b &= q_1r_0 + r_1 \\\
r_0 &= q_2r_1 + r_2 \\\
& \vdots \\\
r_{n-2} &= q_nr_{n - 1} + r_n \\\
r_{n - 1} &= q_{n + 1}r_n
\end{aligned}
$$
其中 $b > r_0 > r_1 > \cdots > r_n$。
可以注意到
$$\gcd(a, b) = \gcd(b, r_0) = \cdots = \gcd(r_{n - 1}, r_n)$$
此式给出了前述的求 $\gcd(a, b)$ 的过程。
扩展欧几里得算法
通过不断地应用公式
$$r_k = r_{k - 2} - q_k r_{k - 1}$$
可以求出可能为负数的 $x, y$,使得 $r_n = ax + by$。
特别地,若 $\gcd(a, b) = 1$,则有 $ax \equiv 1 \pmod b$,即 $x$ 为 $a$ 模 $b$ 的逆元。
int exgcd(int a, int b, int& x, int& y) {
if (b) {
int d = exgcd(b, a % b, y, x);
// d = y * b + x * (a % b)
// = y * b + x * (a - (a / b) * a)
// = y * b + x * a - x * (a / b) * b
// = x * a + (y - x * (a / b)) * b
y -= a / b * x;
return d;
}
x = 1;
y = 0;
return a;
}
例题: 青蛙的约会
有周长为 $L$ 的圆,假设坐标为 $0,1,…,L − 1$,$L − 1$ 的下一个坐标是 $0$。
两只青蛙在圆上,坐标分别为 $x,y$,它们每次都会同时向顺时针方向跳,跳一次的距离分别为 $m,n$,求它们第
一次相遇(落在同一坐标点上)时分别跳了多少次。
所有数均为正整数且均不超过 $2 \times 10^9$
分析:
容易看出题目是在要求我们找到一个最小的 $p$,使得
$$ x+pn \equiv y + pm \pmod L $$
稍微变形一下我们可以得到
$$ p(m-n) + qL = x-y \tag{1} $$
我们首先可以用扩欧计算 $p(m-n)+qL = \gcd(m-n, L)$ 的一组解 $(p, q)$,然后乘上 $\frac{x-y}{\gcd(m-n, L)}$ 就可以得到 $(1)$ 的解。
注意如果 $\gcd(m-n, L) \not\mid (x-y)$ 则无解。
现在我们找到了一组解 $p_0, q_0$ 满足
$$ p_0(m-n) + q_0L = x-y \tag{2} $$
然后我们需要找一组 $p$ 最小的正整数解。
我们观察更一般的情况,即找到了一组解 $x_0, y_0$ 满足
$$ ax_0 + by_0 = \gcd(a, b) \tag{3} $$
在此基础上找一组 $x$ 最小的正整数解。
我们可以将所有的解用这组特殊解表示出来。设一个整数 $k$ 表示增量,那么有
$$ \begin{cases} x = x_0 + k\\\ y = y_0 - \frac{ak}{b} \end{cases} $$
因为 $y$ 是整数,所以有 $b \mid ak$,所以
$$ \frac{b}{\gcd{a, b}} \mid k $$
我们设 $d = \gcd(a, b)$,$k=\frac{bj}{d}$,那么
$$ \begin{cases} x=x_0 + \frac{b}{d} \cdot j \\\ y=y_0 - \frac{a}{d} \cdot j \end{cases} $$
因此将 $x_0$ 对 $\frac{b}{d}$ 取模就可以得到最小的解。
回到原问题:
$$ p_0(m-n) + q_0L = x - y \tag{4} $$
那么答案就是 $p_0 \% \frac{L}{\gcd(m-n, L)}$
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using ll = long long;
int exgcd(ll a, ll b, ll& x, ll& y) {
if (b) {
ll d = exgcd(b, a % b, y, x);
// d = y * b + x * (a % b)
// = y * b + x * (a - (a / b) * a)
// = y * b + x * a - x * (a / b) * b
// = x * a + (y - x * (a / b)) * b
y -= a / b * x;
return d;
}
x = 1;
y = 0;
return a;
}
int main() {
ll a, b, m, n, L;
cin >> a >> b >> m >> n >> L;
ll p, q;
ll d = exgcd(m-n, L, p, q);
if ((b - a) % d) puts("Impossible");
else {
p *= (b - a) / d;
ll t = abs(L / d);
ll ans = p % t;
cout << (ans + t) % t << '\n';
}
return 0;
}
中国剩余定理
求解通与方程组
$$
\begin{cases}
x \equiv a_1 \pmod {m_1} \\\
x \equiv a_2 \pmod {m_2} \\\
\vdots \\\
x \equiv a_n \pmod {m_n}
\end{cases}
$$
其中 $m_1, m_2, \cdots, m_n$ 两两互质。
设 $M = \displaystyle \prod_{i = 1}^n m_i$,可以构造解
$$x = \sum_{i = 1}^n M_i (a_i M_i^{-1} \bmod m_i)$$
其中 $M_i = \frac{M}{m_i}$,可以证明解在模 $M$ 意义下唯一。
上述内容称为中国剩余定理或 $\color{#0000FF}{CRT}$。
扩展CRT
求解同余方程组
$$x \equiv a_i \pmod {m_i}$$
不要求 $m_i$ 两两互质。
将每个方程拆成若干个方程
$$x \equiv a_i \pmod {p_{i,j}^{k_{i,j}}}$$
其中 $m_i = \prod p_{i,j}^{k_{i,j}}$ 为 $m_i$ 的分解式。对每个质数 $p$,合并对应的所有方程,从而转化为模数两两互质的情形。若合并过程中出现矛盾,则原方程组无解。
一些练习题
- Prime Distance
- 质因数分解
- 轻拍牛头 (筛法)
- Sherlock and His Girlfriend
- 樱花
- 上帝与集合的正确用法 (提示:降幂公式)
- 解方程


再添点就可以去考本科数论了hh