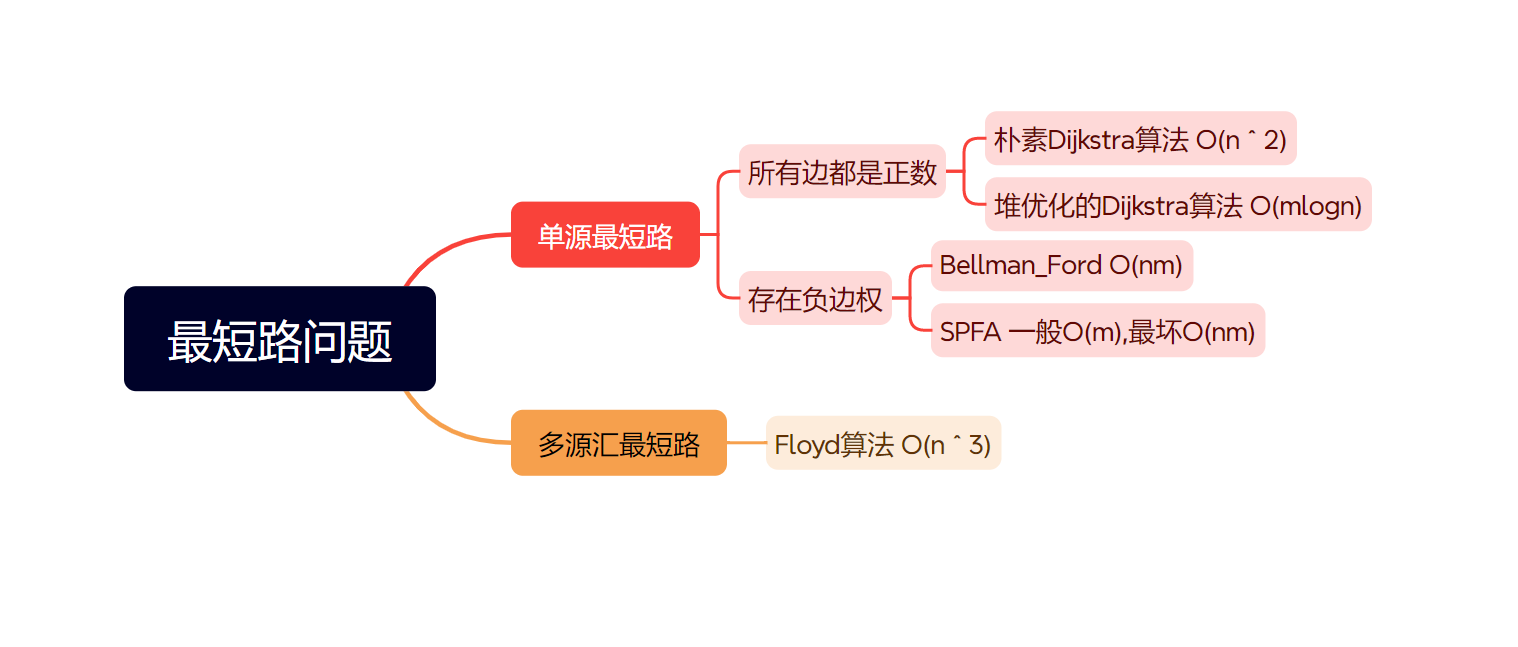
1、Dijkstra算法:每次用离源点最短的边去更新其他边,图中不能存在负权边,否则会破坏性质
int Dijkstra(){
memset(dist, 0x3f , sizeof dist);//初始化距离为无穷大
dist[1] = 0;//源点距离为0
priority_queue<PII,vector<PII>,greater<PII>> heap;//小根堆,vector是存储堆元素的容器
heap.push({0,1});//将源点加入堆中
while(heap.size()){
auto t = heap.top();//获得离源点最近的点
heap.pop();
int ver = t.second, dis = t.first;//ver表示当前节点的序号 dis表示当前节点离源点的 距离
if(st[ver]) continue;//如果该点已经找到了最小距离,则跳过
st[ver] = 1;
for(int i = h[ver]; i != -1; i = ne[i]){//将从该点拓展的节点的距离更新
int j = e[i];//序号
if(dist[j] > dis + w[i]){
dist[j] = dis + w[i];
heap.push({dist[j], j});
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
2、Bellman_Ford算法:非常暴力地去遍历所有地边,每次对边都进行更新,如果更新次数 > n - 1,则说明存在负权回路
下面解释一下为什么Bellman_Ford算法需要遍历 n - 1次:
Bellman-Ford算法是一种用于解决单源最短路径问题的算法,它通过对图中的边进行松弛操作来逐步求解从源点到其他所有顶点的最短路径。
在Bellman-Ford算法中,为了保证找到最短路径,需要进行$n-1$次松弛操作,其中$n$为图中顶点的个数。这是因为在一幅含有$n$个顶点的图中,任意两个顶点之间的最短路径最多包含$n-1$条边。因此,进行$n-1$次松弛操作可以确保找到从源点到所有其他顶点的最短路径。
如果在进行$n-1$次松弛操作后仍然存在可以继续松弛的边,则说明图中存在负权回路,即存在一个环路,使得沿着这个环路走一圈可以让路径的总权值变小。在这种情况下,Bellman-Ford算法会检测到负权回路并报告图中存在负权回路,因为负权回路会导致最短路径无法确定。
因此,进行$n-1$次松弛操作是Bellman-Ford算法的关键步骤,确保找到最短路径并检测负权回路。
void bellman_ford(){
dist[1] = 0;
for(int i = 0 ; i < k; i++){
memcpy(backup, dist, sizeof dist);
for(int j = 1; j <= m; j++){//遍历所有边
int a = Edge[j].a, b = Edge[j].b, w = Edge[j].w;
dist[b] = min(dist[b], backup[a] + w);//注意这里要用上次更新的数据更新,否则会出现串联现象
}
}
}
3、spfa算法:队列优化版的Bellman算法,防止了一些节点无需更新,但是仍然更新的情况
void spfa(){
queue<int> q;
dist[1] = 0;//初始化源点距离
q.push(1);//压入队列
st[1] = 1;//记录已经进入队列
while(q.size()){
int t = q.front();
q.pop();
st[t] = 0;//回溯状态,变为没有进入队列的状态
for(int i = h[t]; i != -1; i = ne[i]){//松弛每个与当前点相连的边
int to = e[i];//点的序号
int val = w[i];//边的权重
if(dist[to] > dist[t] + val){//如果可以距离变得更短,则更新距离
dist[to] = dist[t] + val;
if(!st[to]){//如果当前点不在队列中,则压入队列
q.push(to);
st[to] = 1;
}
}
}
}
}
4、floyd算法: 动态规划的方法计算所有的点之间的最短路,无法处理负环
void floyd(){
for(int k = 1; k <= n; k++)//k表示中间节点
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++){
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}

