跳跃游戏Ⅰ

class Solution {
    public boolean canJump(int[] nums) {
        //我也选择使用一个HashMap来存放区间
        //key是区间的左端点
        //value是区间的右端点
        //其实使用pair也可
        HashMap<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < nums.length; i ++)
        {
            map.put(i, i + nums[i]);
        }



        //其实不需要进行区间合并
        //只有有一个区间的左端点是大于我当前区间的左端点就不可以到达
        int r = 0;
        for(int i = 0; i < nums.length; i ++)
        {
            if(i > r) return false;
            r = Math.max(r, map.get(i));
        }

        return true;
    }
}

跳跃游戏Ⅱ

反着考虑的题解

反着考虑就是从最后一个位置相当于是往前出发，要想走距离远，那么离当前这个点肯定远，因此我们从头往后遍历找第一个能够到达当前我位置的坐标，如果可以更新我就相当于是从后往前跳过去！

这样处理肯定是最短的步数，因为我们对于每一个目标点，我们都是选择跳最远！

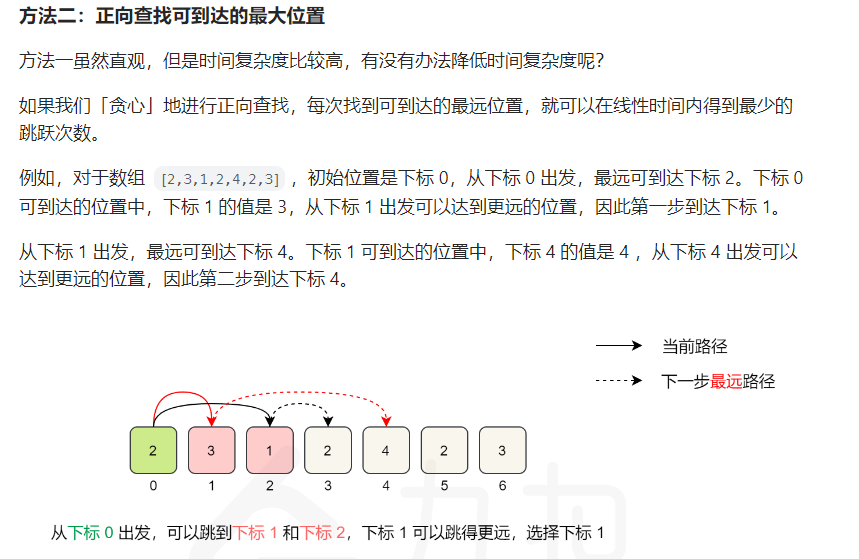
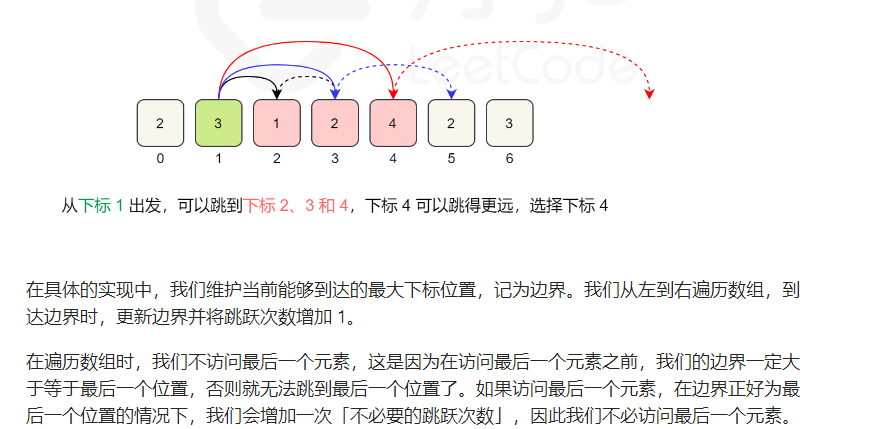
正着考虑的题解

CODE1 反着考虑

class Solution {
    public int jump(int[] nums) {
        int pos = nums.length - 1;
        int step = 0;
        while(pos > 0)
        {
            for(int i = 0; i < pos; i ++)
            {
                if(i + nums[i] >= pos)
                {
                    pos = i;
                    step ++;
                    break;
                }
            }
        }

        return step;
    }
}

CODE1 正着考虑

class Solution {
    public int jump(int[] nums) {

        int length = nums.length;
        int end = 0;
        int maxpos = 0;
        int step = 0;
        for(int i = 0; i < length - 1; i ++)
        {
            maxpos = Math.max(maxpos, i + nums[i]);
            if(i == end)
            {
                end = maxpos;
                step ++;
            }
        }
        return step;
    }
}