Warning:本篇分享只是一个 较复杂方法 的 简单写法,不进行系统的讲解。
前置知识:
- AcWing 242. 一个简单的整数问题
- AcWing 244. 谜一样的牛(树状数组上倍增 解法,蓝书里有讲)
- 会写 权值树状数组。
- 会用
vector水平衡树。(其实就是insert(),erase()常数小) - 会写 权值线段树套下标平衡树。(蓝书也有)
vector 实现的平衡树
namespace Vtree
{
void print(vector<int>& v)
{
for(int i=0;i<(int)v.size();i++)
printf("%d ",v[i]);
printf("\n");
}
void ins(vector<int>& v,int x) { v.insert(lower_bound(v.begin(),v.end(),x),x); }
void del(vector<int>& v,int x) { v.erase(lower_bound(v.begin(),v.end(),x)); }
int count(vector<int>& v,int l,int r)
{
// printf("count(%d ,%d) : ",l,r);
// print(v);
return upper_bound(v.begin(),v.end(),r)-lower_bound(v.begin(),v.end(),l);
}
}
权值线段树套下标平衡树解法:
先咕咕咕了。
…
然后你可能就会想,为什么不把 权值线段树 换成 树状数组 , 把平衡树换成 vector 呢?
-
首先
vector可以实现平衡树(本题需要的)所有操作。- 插入
- 删除
- 查区间元素个数
-
线段树的 查
rank= 树状数组 前缀和. -
线段树的 线段树上二分找 kth = 树状数组倍增找 kth.
权值树状数组套vector 解法
可能配一张图会有助于理解
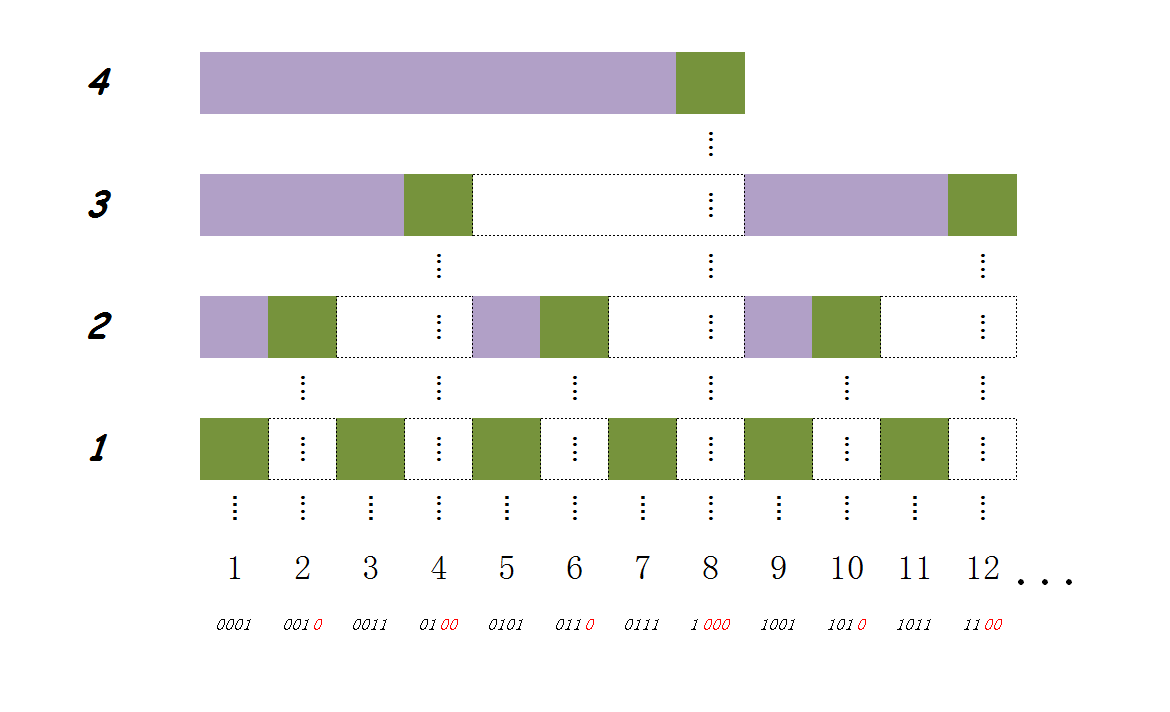
图片来自 https://blog.csdn.net/flushhip/article/details/79165701 侵删。
$v[i]$ 存的是 $a[i] \in [i-lowbit(i)+1,i]$ 的 $i$ ,即下标。
insert
void insert(int pos,int key)
{
for(;key<=num;key+=lowbit(key))
Vtree::ins(v[key],pos);
}
根据定义,在对应的 vector 里加入相应的数。
erase
void erase(int pos,int key)
{
for(;key<=num;key+=lowbit(key))
Vtree::del(v[key],pos);
}
删除操作。
Rank
Rank(x,l,r) 是找 下标在 $[l,r]$ 中有多少个数的 $a[i] \leq x$ 。
对应在树状数组中就是 以 count(v[i],l,r) 为 i 的值,求一遍前缀和即可。
int Rank(int x,int l,int r)
{
int res=0;
for(;x>=1;x-=lowbit(x))
res+=Vtree::count(v[x],l,r);
return res;
}
findkth
findkth(k,l,r) 是找 下标在 $[l,r]$ 中第 k 大的数。
树状数组上倍增即可。
int findkth(int k,int l,int r)
{
static const int lgn=log2(num);
int key=0,sum=0;
for(int i=lgn,y;i>=0;i--) {
y=Vtree::count(v[key+(1<<i)],l,r);
if(sum+y<k && key+(1<<i)<=num) sum+=y,key+=(1<<i);
}
return key+1;
}
这里有两点要注意
- 先跳到目标位置的前一个位置,否则可能会多跳目标位置后的空白段。
- 特判越界的情况。
找 前驱后继 可以用以上两个操作实现,
于是就写完了。
namespace Vtree
{
void ins(vector<int>& v,int x) { v.insert(lower_bound(v.begin(),v.end(),x),x); }
void del(vector<int>& v,int x) { v.erase(lower_bound(v.begin(),v.end(),x)); }
int count(vector<int>& v,int l,int r)
{
return upper_bound(v.begin(),v.end(),r)-lower_bound(v.begin(),v.end(),l);
}
}
inline int lowbit(int x) { return x&(-x); }
void insert(int pos,int key)
{
for(;key<=num;key+=lowbit(key))
Vtree::ins(v[key],pos);
}
void erase(int pos,int key)
{
for(;key<=num;key+=lowbit(key))
Vtree::del(v[key],pos);
}
int Rank(int x,int l,int r)
{
int res=0;
for(;x>=1;x-=lowbit(x))
res+=Vtree::count(v[x],l,r);
return res;
}
int findkth(int k,int l,int r)
{
static const int lgn=log2(num);
int key=0,sum=0;
for(int i=lgn,y;i>=0;i--) {
y=Vtree::count(v[key+(1<<i)],l,r);
if(sum+y<k && key+(1<<i)<=num)
sum+=y,key+=(1<<i);
}
return key+1;
}
AcWing 2476. 树套树
Code:
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<complex>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
namespace Vtree
{
void print(vector<int>& v)
{
for(int i=0;i<(int)v.size();i++)
printf("%d ",v[i]);
printf("\n");
}
void ins(vector<int>& v,int x) { v.insert(lower_bound(v.begin(),v.end(),x),x); }
void del(vector<int>& v,int x) { v.erase(lower_bound(v.begin(),v.end(),x)); }
int count(vector<int>& v,int l,int r)
{
// printf("count(%d ,%d) : ",l,r);
// print(v);
return upper_bound(v.begin(),v.end(),r)-lower_bound(v.begin(),v.end(),l);
}
}
const int N=1e5+5;
int num;
vector<int> v[N];
inline int lowbit(int x) { return x&(-x); }
void insert(int pos,int key)
{
for(;key<=num;key+=lowbit(key)) {
// printf("insert in v[%d], pos = %d\n",key,pos);
Vtree::ins(v[key],pos);
}
}
void erase(int pos,int key)
{
for(;key<=num;key+=lowbit(key))
Vtree::del(v[key],pos);
}
int Rank(int x,int l,int r)
{
// printf("Rank val %d in (%d , %d) = ",x,l,r);
int res=0;
for(;x>=1;x-=lowbit(x))
res+=Vtree::count(v[x],l,r);
// printf("%d\n",res);
return res;
}
int findkth(int k,int l,int r)
{
static const int lgn=log2(num);
int key=0,sum=0;
for(int i=lgn,y;i>=0;i--) {
// printf("count in v[%d], (%d ,%d)\n",key+(1<<i),l,r);
y=Vtree::count(v[key+(1<<i)],l,r);
if(sum+y<k && key+(1<<i)<=num) {
sum+=y,key+=(1<<i);
// printf("Accept %d , now key is %d and sum is %d\n",y,key,sum);
}
}
return key+1;
}
vector<int> nums;
inline int getnw(int x)
{
return upper_bound(nums.begin(),nums.end(),x)-nums.begin();
}
struct Query
{
int opt,x,y,z;
}q[N];
int n,m;
int a[N];
int main()
{
// freopen("1.in","r",stdin);
int i;
int opt,x,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) {
scanf("%d",&a[i]);
nums.push_back(a[i]);
}
for(i=1;i<=m;i++) {
scanf("%d%d%d",&q[i].opt,&q[i].x,&q[i].y);
if(q[i].opt^3) scanf("%d",&q[i].z);
if(q[i].opt^2) {
if(q[i].opt^3) nums.push_back(q[i].z);
else nums.push_back(q[i].y);
}
}
sort(nums.begin(),nums.end());
nums.erase(unique(nums.begin(),nums.end()),nums.end());
num=nums.size()+1;
for(i=1;i<=n;i++)
insert(i,a[i]=getnw(a[i]));
for(i=1;i<=m;i++) {
if(q[i].opt^2) {
if(q[i].opt^3) q[i].z=getnw(q[i].z);
else q[i].y=getnw(q[i].y);
}
}
for(i=1;i<=m;i++) {
opt=q[i].opt; x=q[i].x; y=q[i].y; z=q[i].z;
if(opt==1) printf("%d\n",Rank(z-1,x,y)+1);
else if(opt==2) printf("%d\n",nums[findkth(z,x,y)-1]);
else if(opt==3) erase(x,a[x]),insert(x,a[x]=y);
else if(opt==4) {
int t=Rank(z-1,x,y);
if(t==0) puts("-2147483647");
else printf("%d\n",nums[findkth(t,x,y)-1]);
}
else {
int t=Rank(z,x,y);
if(t==y-x+1) puts("2147483647");
else printf("%d\n",nums[findkth(t+1,x,y)-1]);
}
}
return 0;
}
性能分析:
由于使用了vector当平衡树,时间复杂度不好分析,
空间复杂度是 $O(nlogn)$,
这种解法在洛谷的树套树中,是最优解第一面中代码最短的。可以说,在分块遍地开花的世界中独树一帜了。
进步性:代码短、快,便于调试。
局限性:树状数组的空间受限于值域,如果强制在线,并且值域很大的话,就不能用这种方法来维护了。


关注了
tql