题目大意：有一些工作需要做，每个工作又开始时间和结束的时间，每台机器每次只能做一个工作，但是一旦机器开启在所有工作完成之后就不能停止，现在给你一些工作的开始时间和结束时间求出最少需要多少台机器才能完成这些任务最少的时间。

贪心 + multiset
我们需要注意的是，机器在打开后就停不下来，最短时间需要加上待机时间

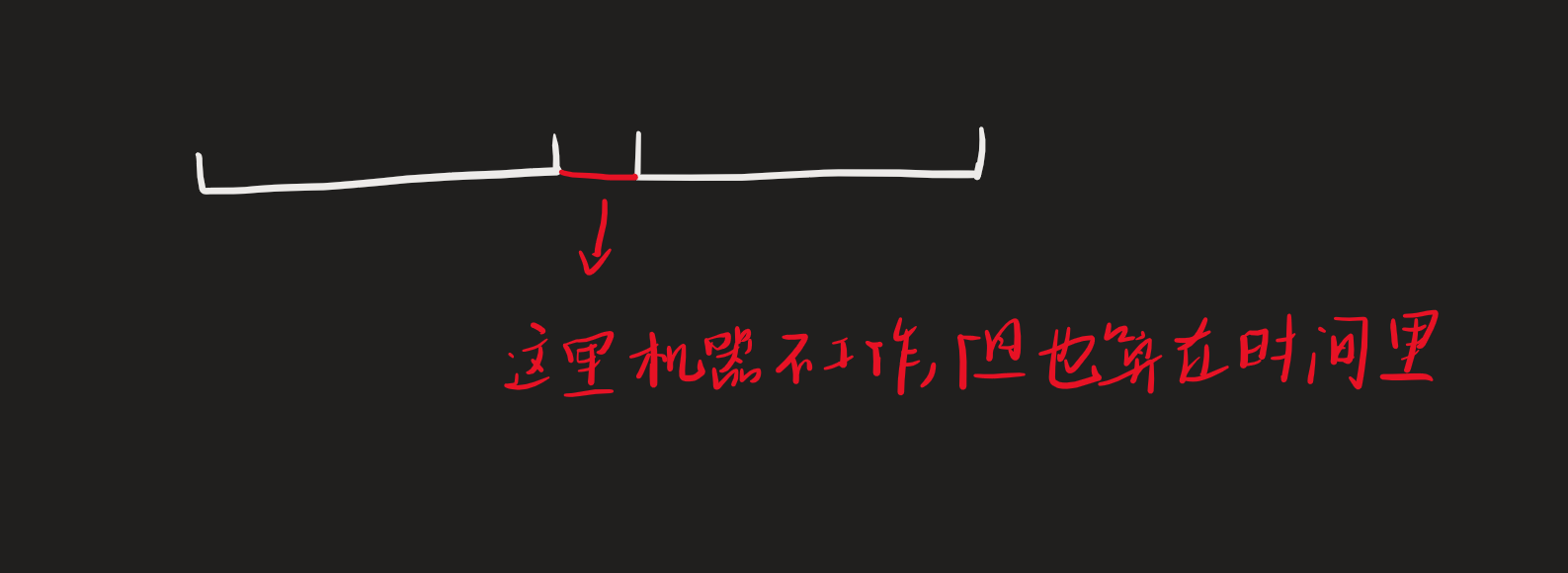
思路：对每个区间按照左端点大小进行排序，之后找每个区间的左端点是否大于等于已有组合的右端点，如果有则并入组合，如果没有则需要加一个组合，与贪心专题中的906.区间组合问题相似

#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int n;
typedef long long ll;
struct Range
{
    ll l, r;
    bool operator<(const Range &s) const
    {
        return l < s.l;
    }
} range[N];
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n;
        ll res = 0, sum = 0;
        for (int i = 0; i < n; i++)
        {
            cin >> range[i].l >> range[i].r;
        }
        sort(range, range + n);
        multiset<ll> s;
        for (int i = 0; i < n; i++)
        {
            auto x = range[i];
            if (s.empty())
            {
                s.insert(x.r);
                res++;
                sum += x.r - x.l;
                continue;
            }
            auto tmp = s.upper_bound(x.l);
            if (tmp == s.begin())
            { // 最小的r都大于x.l,则增加一个区间
                res++;
                sum += x.r - x.l;
                s.insert(x.r);
            }
            else{//可以合并进一个组合，加入这个组合,并更新这个组合的右区间值
                tmp--;
                sum += x.r - *tmp;//记得把待机时间也要加上
                s.erase(tmp);
                s.insert(x.r);
            }
        }
        cout << res << " " << sum << endl;
    }
    return 0;
}