#include<iostream>
using namespace std;
const int N =100000010;
int primes[N],cnt;
bool st[N];
void get_primes(int n)
{
    for(int i=2;i<=n;i++)//既是倍数，也是每一个数本身。
    {
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++)
        {
            st[primes[j]*i]=true;//确保筛掉每一个合数
            if(i%primes[j]==0) break;//确保是被最小的质数筛掉。
        }
    }
}
int main() 
{
    int n;
    cin>>n;
    get_primes(n);
    cout<<cnt<<endl;
    return 0;
}

讲一下个人对于线性筛代码的理解
1.首先明确一点，一个数一定可以分解成质数和其他数的乘积。同时分解成的质数和其他数一定是小于等于该数的。
2.高中时有一个定理一个数可以分解成一大一小的两个数的乘积（忘记原话时什么了），当然这两个数也可以相等。

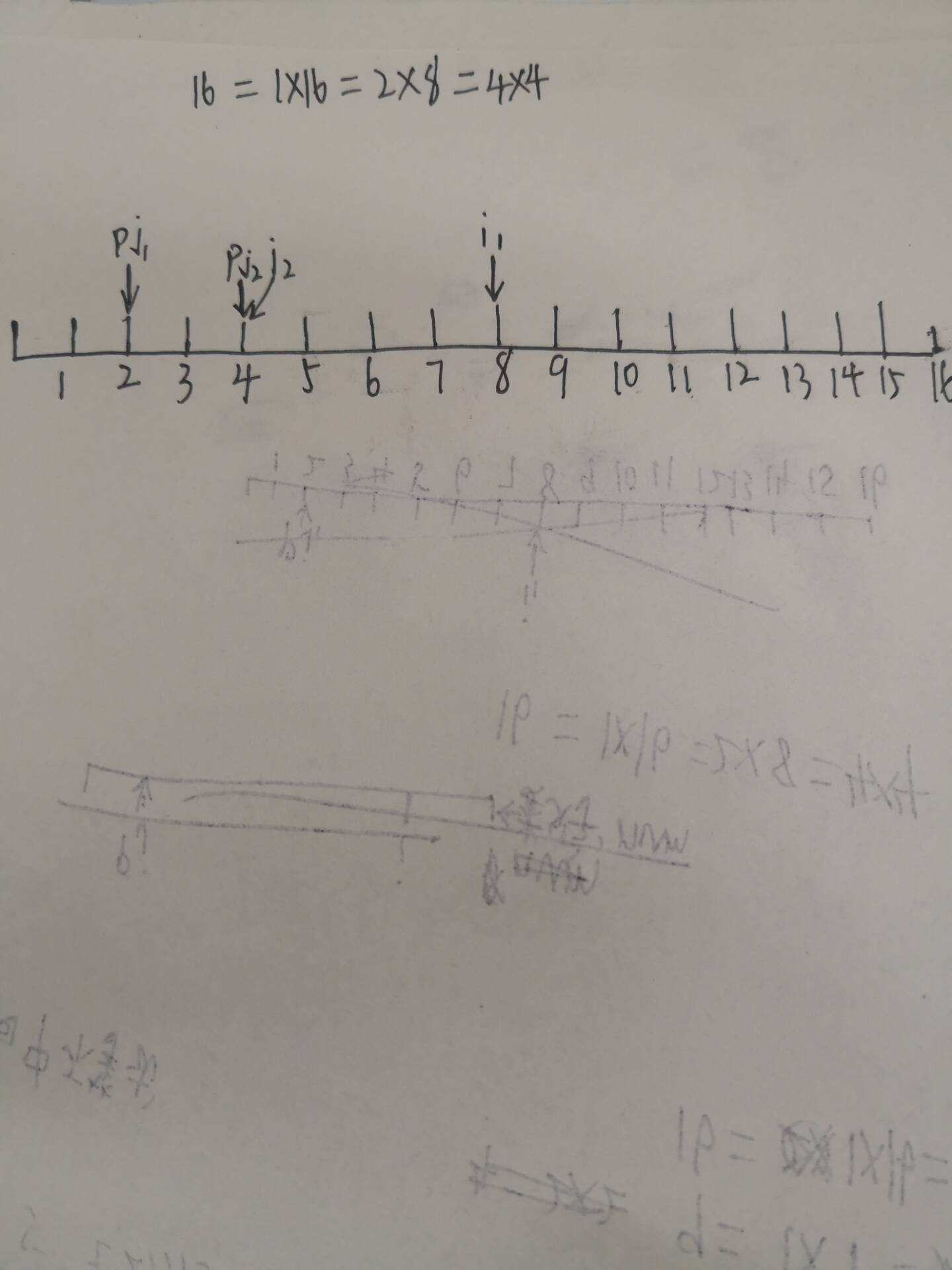
综合以上两点，那么我们可以得出一个结论：一个数分解成最小质因子和其他数的乘积的话，其他数一定是大于等于最小质因子的。该话对应下面这段代码。

 st[primes[j]*i]=true;//确保筛掉每一个合数

所以当我们遍历到一个数的时候，该数不是合数的话就说明当前数是质数。对应下面这段代码。

if(!st[i]) primes[cnt++]=i;

对于下面这段代码，我的理解是：
1.如果该语句执行，说明之前该数（也就是i）已经被他的最小质因子筛过了。
2.i可以整除他的最小质因子，i就是他的最小质因子的倍数，那么再用i乘其他质数筛数就会导致后面重复筛选。
就比如12本可以被4 * 3筛选掉 4 = 2 * 2 * 3，但是实际上4是2的倍数，那么12肯定可以被2的某一个倍数筛掉。

if(i%primes[j]==0) break;//确保是被最小的质数筛掉