首先呢,图在遍历之前得先存储
知周所众,树就是一种特殊的图
所以我们先来讨论图的存储
而所众知周,无向图就是一种特殊的有向图,所以我们只需要谈论有向图的存储就行了。
图的存储有两种方式:
- 邻接矩阵
- 邻接表
邻接矩阵
其实就是开一个二维数组,$g[u][v]$代表$u$到$v$有一条边,这种方法有点缺陷,就是数据范围太大的时候没法用,而且不能存重边。
上一篇DFS与BFS中的走迷宫就用的这种方法。
这种方法比较适合存储稠密图。
邻接表
跟哈希表中的拉链法一模一样,不信回去看。
如果点$u$连向了点$v$,就在$u$那条链上栓一个$v$。
它什么图基本上都能存。
邻接表的代码参考哈希表就行。
然后就是图的遍历了
深度优先遍历(DFS):
他跟搜索的那个深度优先遍历一模一样,就比如说有这样一张图:
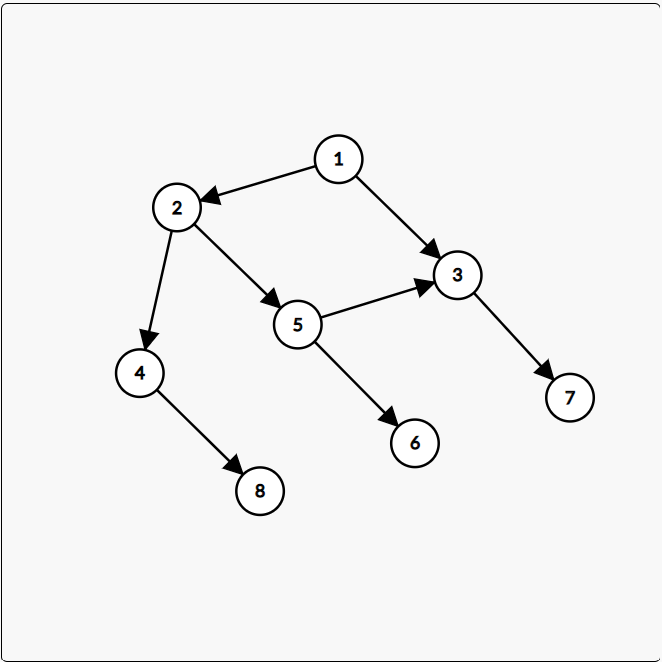
它的深度优先遍历顺序就是这样的:
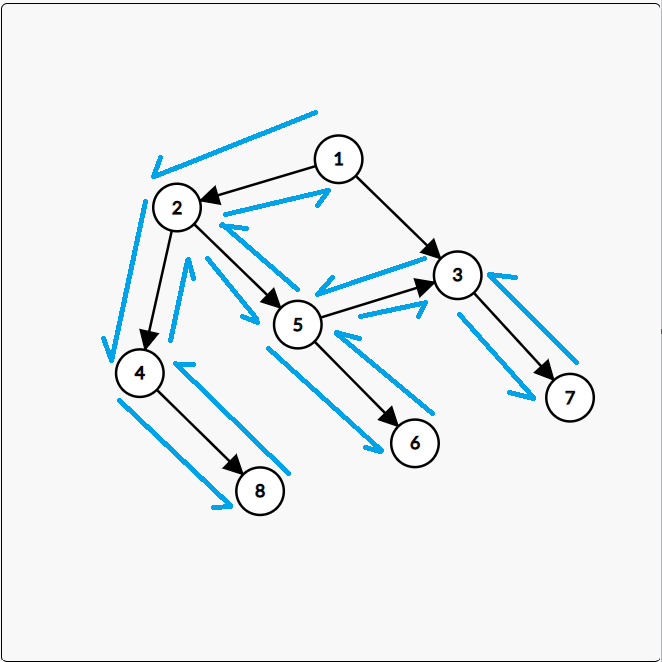
就是一条道走到黑,然后再回溯。
看树的重心这道题。
大体意思就是把树尽可能碎乎的拆开。可以遍历每一个点,然后求出答案,最后输出最小的就行了。
int dfs(int u){ // 返回以u为根节点的所有子树中点的数量
b[u] = true;
int size = 0, sum = 0; // size表示假如删除u这个点,那么剩下连通块中点最多的联通块中点的数量。sum表示以u为根节点的子树中点的数量(不包含自己所以最后要加一)。
for (int i = h[u]; ~i; i = ne[i]){
int t = e[i];
if (!b[t]){
int s = dfs(t);
size = max(size, s);
sum += s;
}
}
size = max(size, n - sum - 1);
daan = min(size, daan);
// 先把所有字数重点的数量求最大值,再与答案求最小值。
return sum + 1;
}
宽度优先遍历(BFS):
他跟搜索的那个深度优先遍历一模一样,就比如说有这样一张图:

它的宽度优先遍历顺序就是这样的(数字表示是第几次遍历到的):
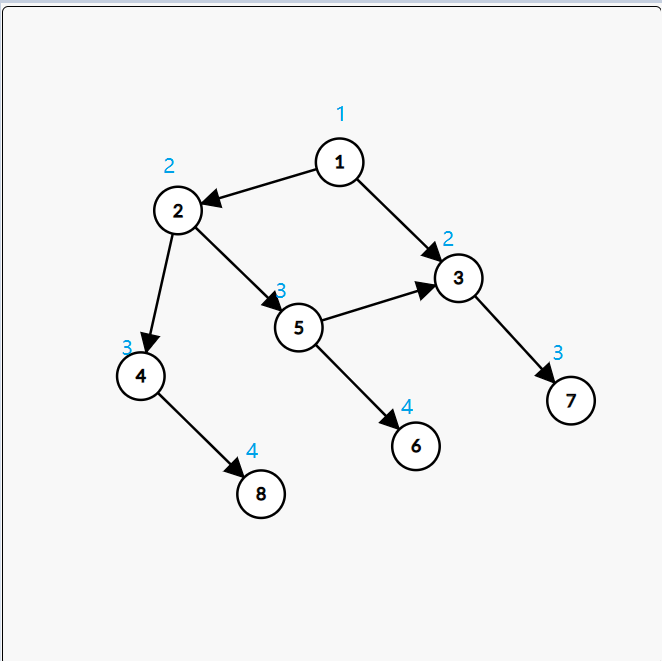
每一次遍历到的点都是上一次遍历到的点所有出边对应的点(被标记的不行)。
看图中点的层次这道题。
就用BFS的板子就行了。
int bfs(){
memset(d, -1, sizeof d);
q.push(1);
d[1] = 0;
while(!q.empty()){
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]){
int j = e[i];
if (!(~d[j])){
d[j] = d[t] + 1;
q.push(j);
}
}
}
return d[n];
}
好,到现在就结束了……个嘚儿啊,BFS还有一种应用叫拓扑序,然后来说一下拓扑序:
首先,拓扑序只在有向图中生效。
假设有这么一张有向图:
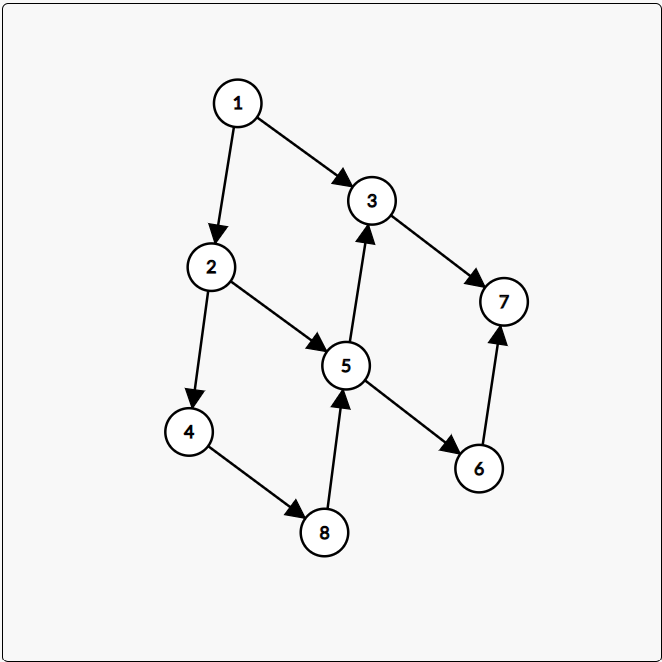
拓扑序,就是把入度为零的点加进序列中然后删掉,一直这么操作,直到把图清空。
当然,只要图中有环,那么就没法弄出拓扑序,所以拓扑序也可以用来判环。
就比如上面那张有向图,它没有环,所以是有拓扑序的。
可以发现,一直照上面的操作,中途会得到这样的东西(上面代表图,下面代表已求出的拓扑序):
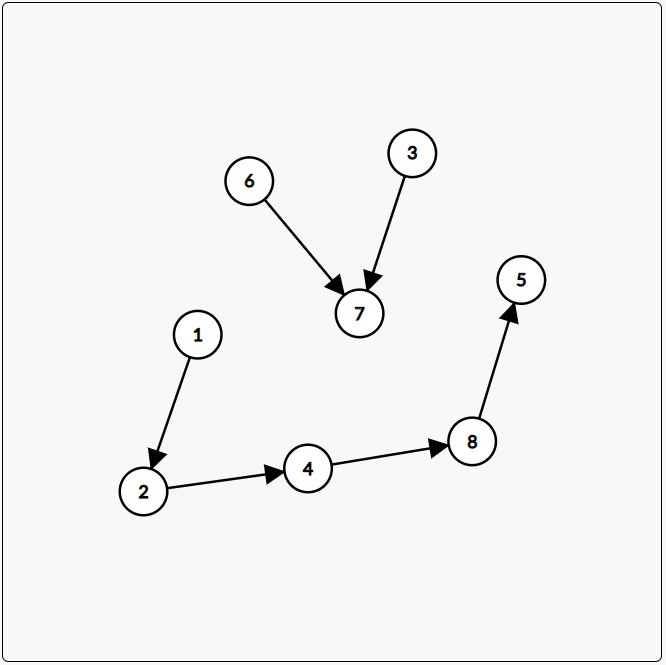
这样会有两种拓扑序,分别是:
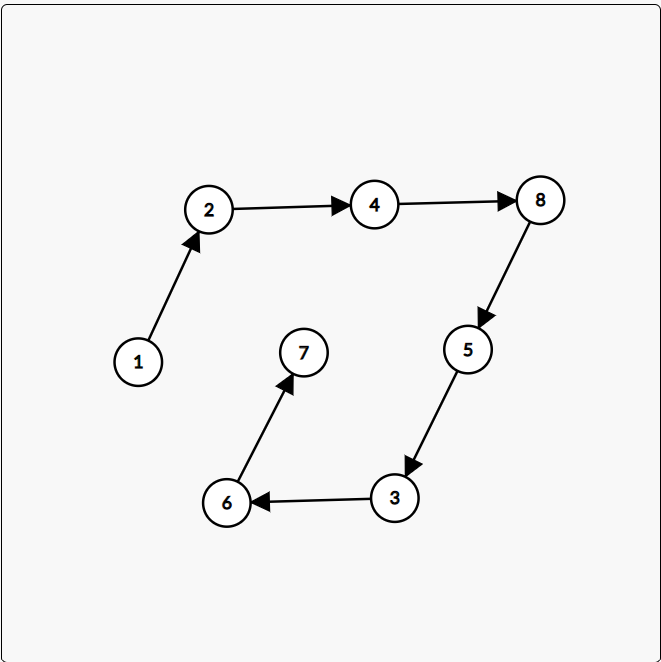
和:
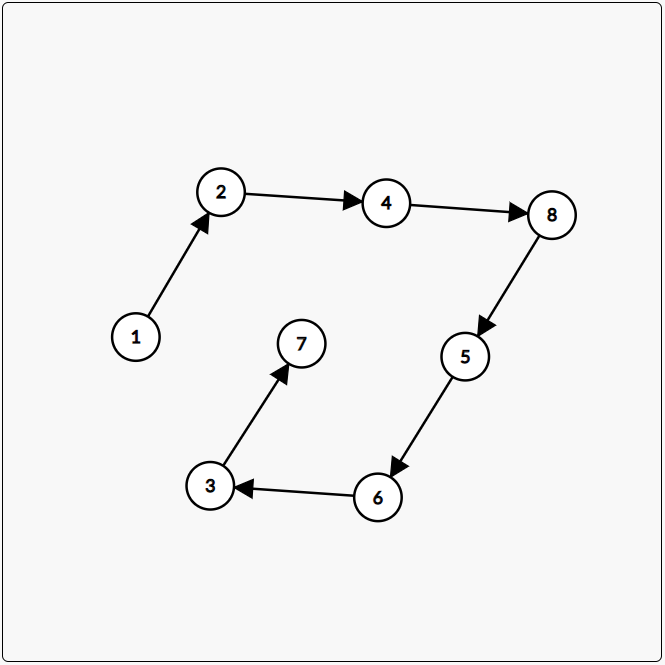
都是可以的。
一个图按拓扑序排好后,所有边都是从前指向后的。
根据种种原因,有向无环图也被称为拓扑图。
然后解释一下用到的名词,出度的意思就是他一共指向了几个点,入度的意思就是有几个点指向这个点。
然后我们来看一下怎么求拓扑序。
先用一个队列存所有入度为零的点,再用BFS的方法,让所有队列里的点所有的出度对应的点的入度减一。直接用宽搜的板子写就行了。
板子题:有向图的拓扑序列
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m, d[N], q[N];
int h[N], e[N], ne[N], idx;
void add(int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
bool topsort(){
int hh = 0, tt = -1;
for (int i = 1; i <= n; i ++ ){
if (!d[i])
q[++tt] = i;
}
while (hh <= tt){
int t = q[hh++];
for (int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if (--d[j] == 0)
q[++tt] = j;
}
}
return tt == n - 1;
}
int main(){
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ ){
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
d[b]++;
}
if (!topsort()) puts("-1");
else
for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
return 0;
}
请原谅我又双叒叕抄了y总的代码(并改了码风)。

