并查集

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的合并及查询 问题.它支持两种操作：
查找（Find）：确定某个元素处于哪个子集；
合并（Union）：将两个子集合并成一个集合。

基本原理

并查集的重要思想在于，用集合中的一个元素代表集合。并查集由一群集合构成，最开始时所有元素各自单独构成一个集合。比如，有一批元素arr = [a, b, c, d, e]，我们需要将这一批元素初始化成单个元素的集合，即a单独构成一个集合，b单独构成一个集合。其中并查集中的单个集合结构如下所示：

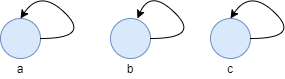
当集合中只有一个元素时，这个元素的父节点为自己，也就是这个集合的代表节点。当一个集合有多个节点时，代表节点为集合中父节点指向其自己的节点，比如下图的节点a。

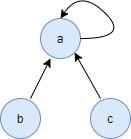
初始化

for (int i = 0; i < n; i++) fa[i] = i;  // i就在它本身的集合里

查找

通俗地讲一个故事：几个家族进行宴会，但是家族普遍长寿，所以人数众多。由于长时间的分离以及年龄的增长，这些人逐渐忘掉了自己的亲人，只记得自己的爸爸是谁了，而最长者（称为「祖先」）的父亲已经去世，他只知道自己是祖先。为了确定自己是哪个家族，他们想出了一个办法，只要问自己的爸爸是不是祖先，一层一层的向上问，直到问到祖先。如果要判断两人是否在同一家族，只要看两人的祖先是不是同一人就可以了。
在这样的思想下，并查集的查找算法诞生了。
代码实现:

int fa[MAXN];  // 记录某个人的爸爸是谁，特别规定，祖先的爸爸是他自己
int find(int x) {
  // 寻找x的祖先
  if (fa[x] == x)  // 如果x是祖先则返回
    return x;
  else
    return find(fa[x]);  // 如果不是则x的爸爸问x的爷爷
}

显然这样最终会返回x的祖先。这样的确可以达成目的，但是显然效率实在太低。为什么呢？因为我们使用了太多没用的信息，我的祖先是谁与我父亲是谁没什么关系，这样一层一层找太浪费时间，不如我直接当祖先的儿子，问一次就可以出结果了.
路径压缩

把在路径上的每个节点都直接连接到根上,这就是路径压缩。

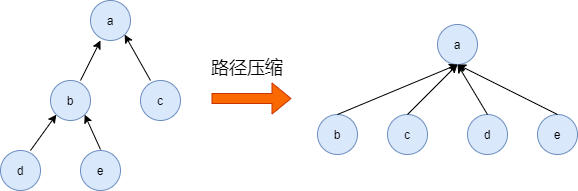
代码实现

int find(int x) {
  if (x != fa[x])  // x不是自身的父亲，即x不是该集合的代表
    fa[x] = find(fa[x]);  // 查找x的祖先直到找到代表,于是顺手路径压缩
  return fa[x];
}

合并

宴会上，一个家族的祖先突然对另一个家族说：我们两个家族交情这么好，不如合成一家好了。另一个家族也欣然接受了,我们之前说过，并不在意祖先究竟是谁，所以只要其中一个祖先变成另一个祖先的儿子就可以了。

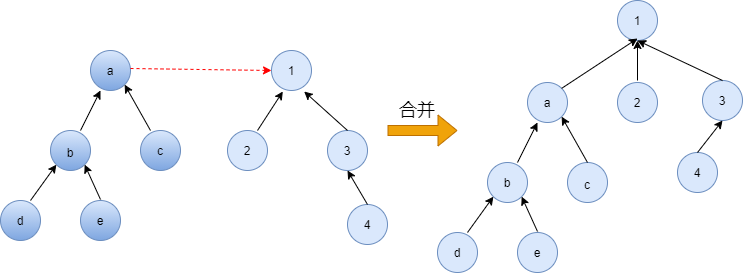
代码实现

// x 与 y 所在家族合并
  x = find(x);
  y = find(y);
  fa[x] = y;  // 把 x 的祖先变成 y 的祖先的儿子

以上就是并查集的基本操作了,同时并查集还可以维护一些额外信息.这里我们附上代码模板
维护size的并查集：

 int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);

维护到祖宗节点距离的并查集：

 int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

相关题目:
ACwing 836.合并集合
Acwing 837.连通块中点的数量

参考资料
算法基础课
oi wiki