堆

堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。
每个节点的键值都大于等于其父亲键值的堆叫做小根堆，否则叫做大根堆。

堆主要支持的操作有：

插入一个数、查询最小值、删除最小值、删除任意元素、修改一个元素的值。

堆的存储

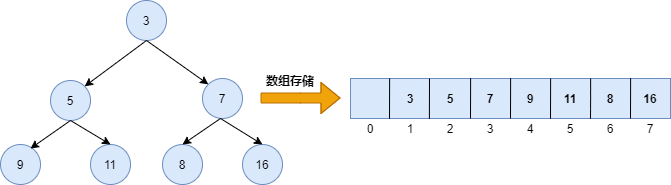
用一维数组存储,0号位置不存储元素.1号元素是根节点,对于节点p,p*2即为左儿子,p*2+1即为右儿子。同时,用size记录当前二叉堆中节点的个数。

堆的构建

// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;
// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);

功能的实现

• down(x)，将节点往下移，在该结点的儿子中，找一个最小的，与该结点交换，重复此过程直到底层;
  代码实现:

void down(int u)
{
    int t = u; //存储u
    //如果有左儿子,并且左儿子比自己小,则将左儿子的下标赋给t
    if (u * 2 <= size && h[u * 2] < h[t])  t = u * 2; 
     //如果有右儿子,并且右儿子更小,则将右儿子的下标赋给t
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    //交换
    if (u != t)
    {
        swap(u, t);
        down(t);
    }
}

• up(x)，如果这个结点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根;
  代码实现

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(u, u / 2);
        u >>= 1;
    }
}

后面的功能都可以用上面两个基本操作来实现

1. 在堆的末尾插入一个值：heap[size++]=x,up(size)，最小值heap[1]；
2. 删除最小值，用堆的最后一个元素覆盖第一个元素，heap[1]=heap[size],size–,down(1),（因为尾节点比头节点更容易删除）;
3. 删除任意一个元素，heap[k]=heap[size],size–,down(k),up(k);
4. 修改任意一个元素，heap[k]=x,down(x),up(x);

相关题目
ACwing 838.堆排序
ACwing 839.模拟堆
参考资料
算法基础课
oi wiki