原理

以在一个升序数组中查找一个数为例。
它每次考察数组当前部分的中间元素，如果中间元素刚好是要找的，就结束搜索过程；
如果中间元素小于所查找的值，那么左侧的只会更小，不会有所查找的元素，只需到右侧查找；
如果中间元素大于所查找的值同理，只需到左侧查找。

时间复杂度

二分查找的最优时间复杂度为O(1) 。
二分查找的平均时间复杂度和最坏时间复杂度均为 O(logn)。
因为在二分搜索过程中，算法每次都把查询的区间减半，所以对于一个长度为n的数组，至多会进行O(logn)次查找。

空间复杂度

迭代版本的二分查找的空间复杂度为O(1)。
递归（无尾调用消除）版本的二分查找的空间复杂度为O(logn)。

整数二分

算法思路：假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。
二分流程

1.确定二分的边界
2.编写二分的代码框架
3.设计一个check函数(性质)
4.判断一下区间如何更新
5.如果更新方式写的是l=mid,r=mid-1,那么就在算mid的时候加上1

模板1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        //if的判断条件是让mid落在满足你想要结果的区间内
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    //出循环一定是l == r，所以l和r用哪个都可以
    return l;
}

模板2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        //if的判断条件是让mid落在满足你想要结果的区间内
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    //出循环一定是l == r，所以l和r用哪个都可以
    return l;
}

二分技巧

什么题可以使用二分
有序

注意，这里的有序是广义的有序，如果一个数组中的左侧或者右侧都满足某一种条件，而另一侧都不满足这种条件，也可以看作是一种有序（如果把满足条件看做1，不满足看做0，那么像这样0000011111,00011100,1100000这些区间为有序）。

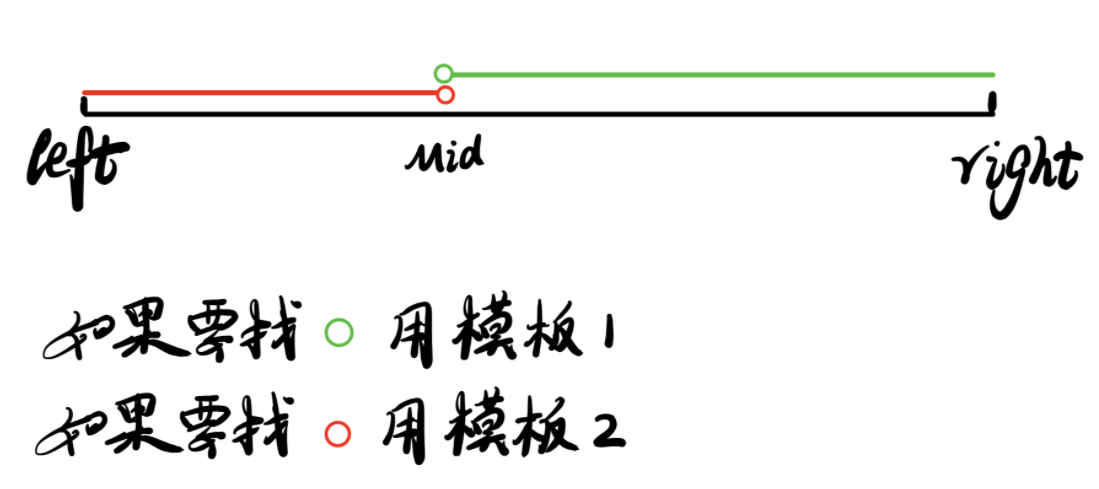
什么时候用哪个模板
来自Anish大佬
二分只有下面两种情况
1：找大于等于给定数的第一个位置 （满足某个条件的第一个数）
2：找小于等于给定数的最后一个数 （满足某个条件的最后一个数）

check函数的设计

具体问题具体分析(逃

相关题型
ACwing 14.不修改数组找出重复的数字
ACwing 789.数的范围
ACwing 790.数的三次方根
ACwing 1227. 分巧克力
ACwing 730.机器人跳跃问题
ACwing 680.剪绳子
ACwing 1236.递增三元组

参考资料
ACwing
oi wiki
Anish