树上差分

前置知识

$lca $ (最近公共祖先)

在一棵树上，两个节点最近的公共父节点。$LCA(a, b)$

想要实现这个函数必须事先预处理出两个数组

1. $depth[i]$ 数组，处理出$i$节点的深度 （==就是该节点到根节点的距离==）
2. $fa[i]$ 数组，就是$i$节点的父节点

接下来，我们就可以通过,先将深度神的节点走到深度浅的节点，然后将两个节点同时走到 他们最近的公共祖先。

#### 这样就结束了

但是这样有很明显的缺点就是时间复杂度太大了，那么我们应该怎么优化呢？？

对！ 就是用倍增的算法，在追溯父节点的时候，用倍增的跳跃，这样就得再接着预处理出一个数组，或者说给$fa[]$ 数组改良一下

1. $fa[i][j]$ 用于存储该节点向上跳跃 $2 ^ j$​ 的节点是谁。

那么到这里就结束了，详细的实现就不过多介绍，直接看代码

void dfs(int u) {
  for (int i = 1; (1 << i) < dep[u]; i++) {
    dp[u][i] = dp[dp[u][i - 1]][i - 1];
  }
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (st[j]) continue;
    st[j] = 1;
    dep[j] = dep[u] + 1;
    dp[j][0] = u;
    dfs(j);
  }
  return;
}

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);

  int k = log2(dep[a] - dep[b]);

  for (int i = k; i >= 0; i--) {
    if (dep[dp[a][i]] >= dep[b]) a = dp[a][i];
  }
  if (a == b) return a;

  k = log2(dep[a]);
  for (int i = k; i >= 0; i--) {
    if (dp[a][i] == dp[b][i]) continue;
    a = dp[a][i];
    b = dp[b][i];
  }
  return dp[a][0];
}

点权差分

P3128 [USACO15DEC]Max Flow P

题目大意

给出一棵树，奶牛可以从a,走到 b，判断走过所有路径后，树上的每个点被走过几次？

思路

先处理一个数组$d[i]$ 表示一个点被走过多少次

• 很明显，若是两个点都在一条没有分叉点的路线上，那么它就与正常差分无异，我们只需要

​ d[a]++ , d[fa[b][0]]--

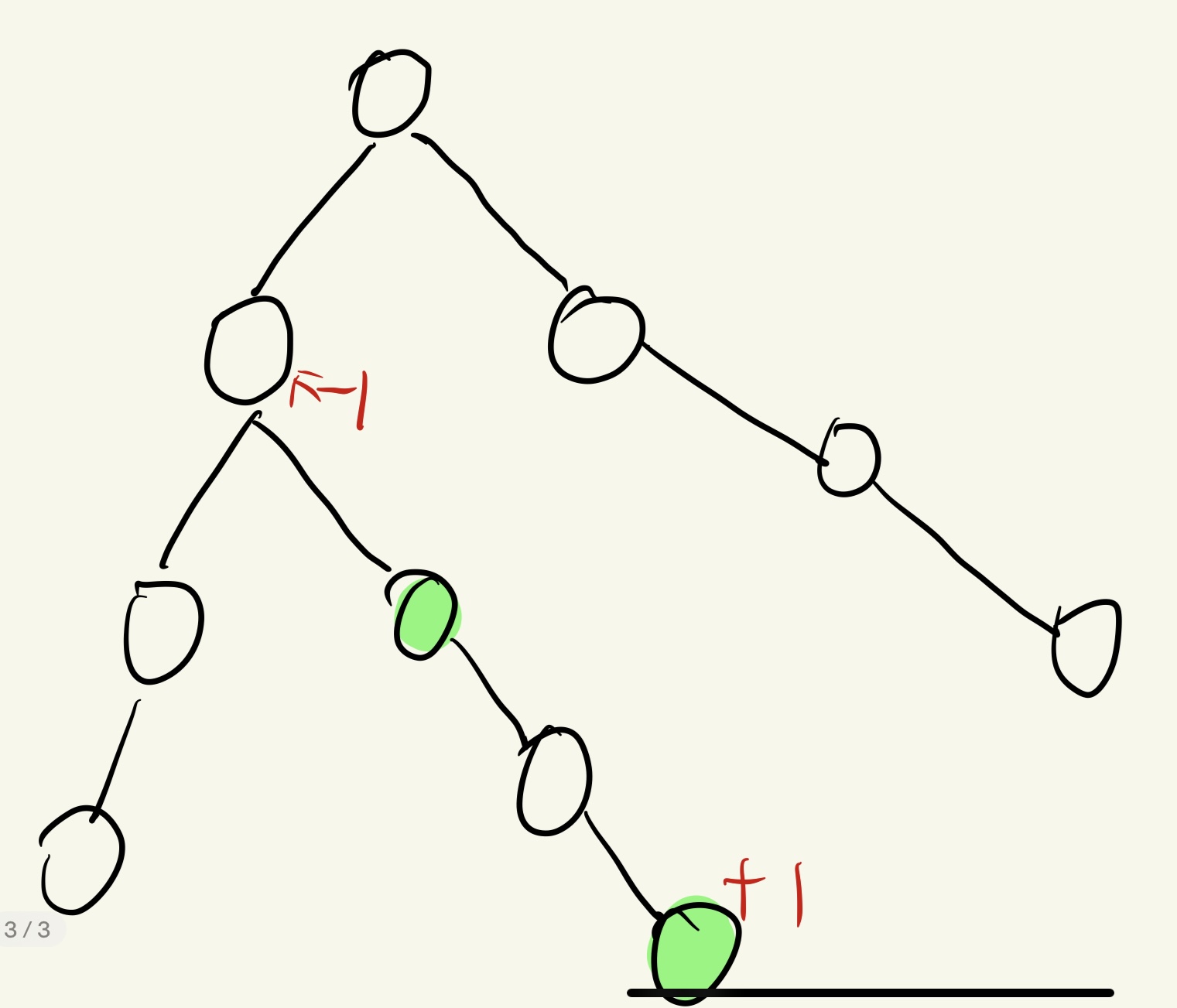
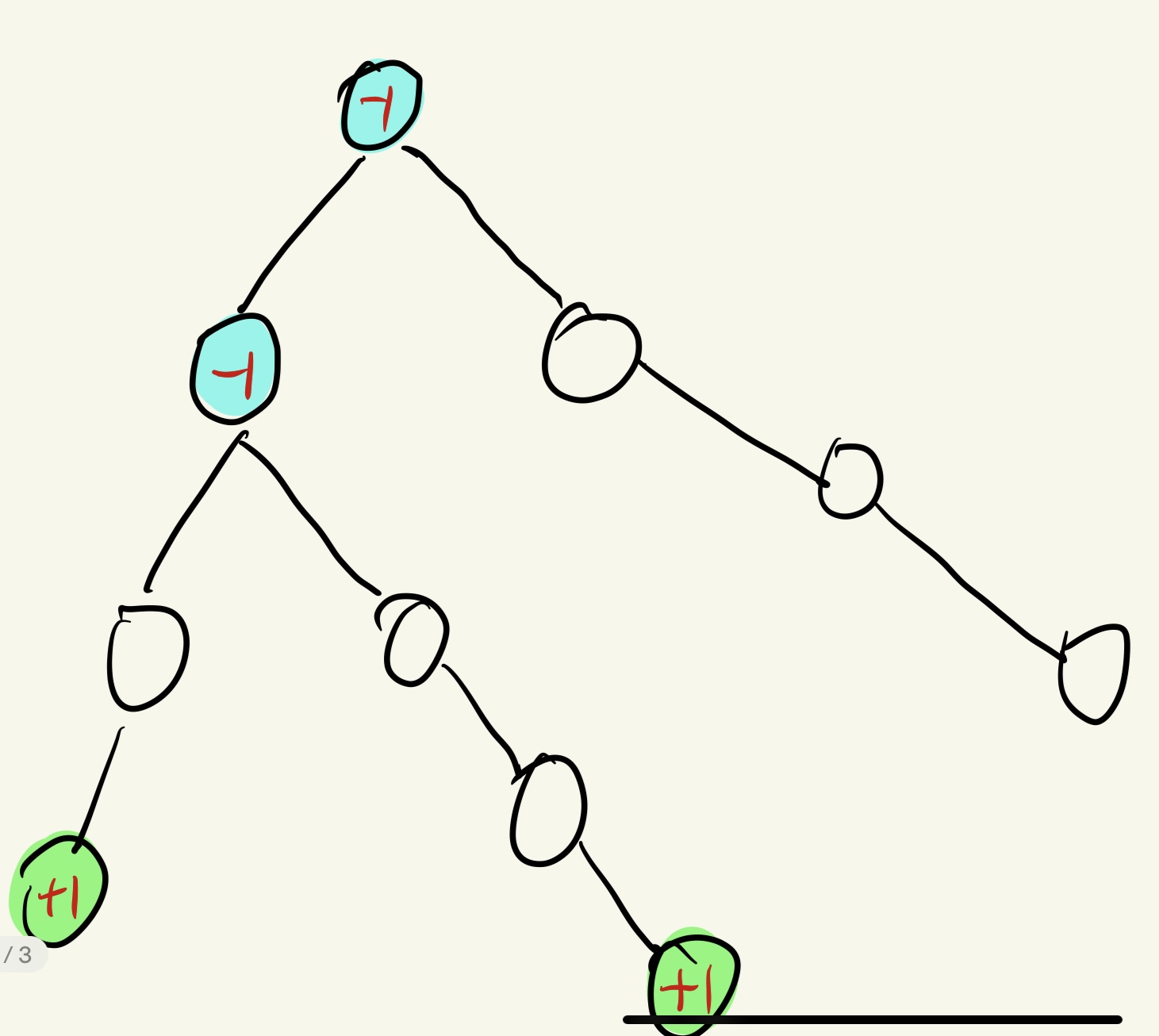
• 但若是两个点中间有一个公共的父节点，那么 $lca(a,b)$ 就会被多加一次1,那么我们就得在该节点的父节点减去一个1，即使这样$lca(a,b)$之上的节点还是会被多加一次1，我还还需要再$lca(a,b)$的父节点减去1这样该公共祖先之上的节点就不会多加1.

d[a] ++, d[b] ++ , d[fa[lca(a,b)][0]] --, d[lca][0] --

上代码

// Problem: C. Arrow Path
// Contest: Codeforces - Educational Codeforces Round 163 (Rated for Div. 2)
// URL: https://codeforces.com/contest/1948/problem/C
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

#define inf 0x3f3f3f3f
#define pii pair<int, int>
#define lowbit(x) x&(-x)
using namespace std;
const int N = 1e5 + 10;
const int mod = 1e9 + 7;
#define int long long
const double pie = 3.1415926;

int dp[N][38];
int dep[N];
int e[N], ne[N], h[N], idx;
bool st[N];
int d[N];
int ans = 0;
void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }

int dfs1(int u, int fa) {
  int res = d[u];
  // cout << res << endl;
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (j != fa) {
      int s = dfs1(j, u);
      res += s;
    }
  }
  ans = max(ans, res);
  return res;
}

void dfs(int u) {
  for (int i = 1; (1 << i) < dep[u]; i++) {
    dp[u][i] = dp[dp[u][i - 1]][i - 1];
  }
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (st[j]) continue;
    st[j] = 1;
    dep[j] = dep[u] + 1;
    dp[j][0] = u;
    dfs(j);
  }
  return;
}

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);

  int k = log2(dep[a] - dep[b]);

  for (int i = k; i >= 0; i--) {
    if (dep[dp[a][i]] >= dep[b]) a = dp[a][i];
  }
  if (a == b) return a;

  k = log2(dep[a]);
  for (int i = k; i >= 0; i--) {
    if (dp[a][i] == dp[b][i]) continue;
    a = dp[a][i];
    b = dp[b][i];
  }
  return dp[a][0];
}

void solve() {
  int n, k;
  cin >> n >> k;
  memset(h, -1, sizeof h);
  for (int i = 1; i <= n - 1; i++) {
    int a, b;
    cin >> a >> b;
    add(a, b);
    add(b, a);
  }
  dfs(1);

  for (int i = 0; i < k; i++) {
    int a, b;
    cin >> a >> b;
    int p = lca(a, b);

    d[a]++, d[b]++, d[p]--, d[dp[p][0]]--;
  }
  // for (int i = 1; i <= n; i++) cout << dep[i] << " \n"[i == n];
  dfs1(1, -1);
  cout << ans << endl;
}

#undef int
int main() {
  cout << fixed << setprecision(3);
  int t = 1;
  // cin >> t;
  int tt = t;
  while (t--) {
    // cout << "Case #" << tt - t << ": ";
    solve();
    // cout << endl;
  }
  return 0;
}

边权差分

闇の連鎖

题目大意

• 给出 $n - 1$ 条主要边， 然后再给出 $k$ 条附加边，
• 主要边 ： 可供构成一棵树的 $n - 1$ 条边。
• 附加边 ： 除了 $n - 1$ 条边之外的所有边 ———可以理解为附加边将一条路径连成了一个环。
• 给你两次操作，先删除一条 主要边 , 然后删除一条 附加边 ，要求使得将这棵树分割成两

思路

我们可以想到对每个 主要边 求贡献值，然后累加起来，就是最后的答案。

那么应该怎么求出一条主要边的贡献值呢 ——

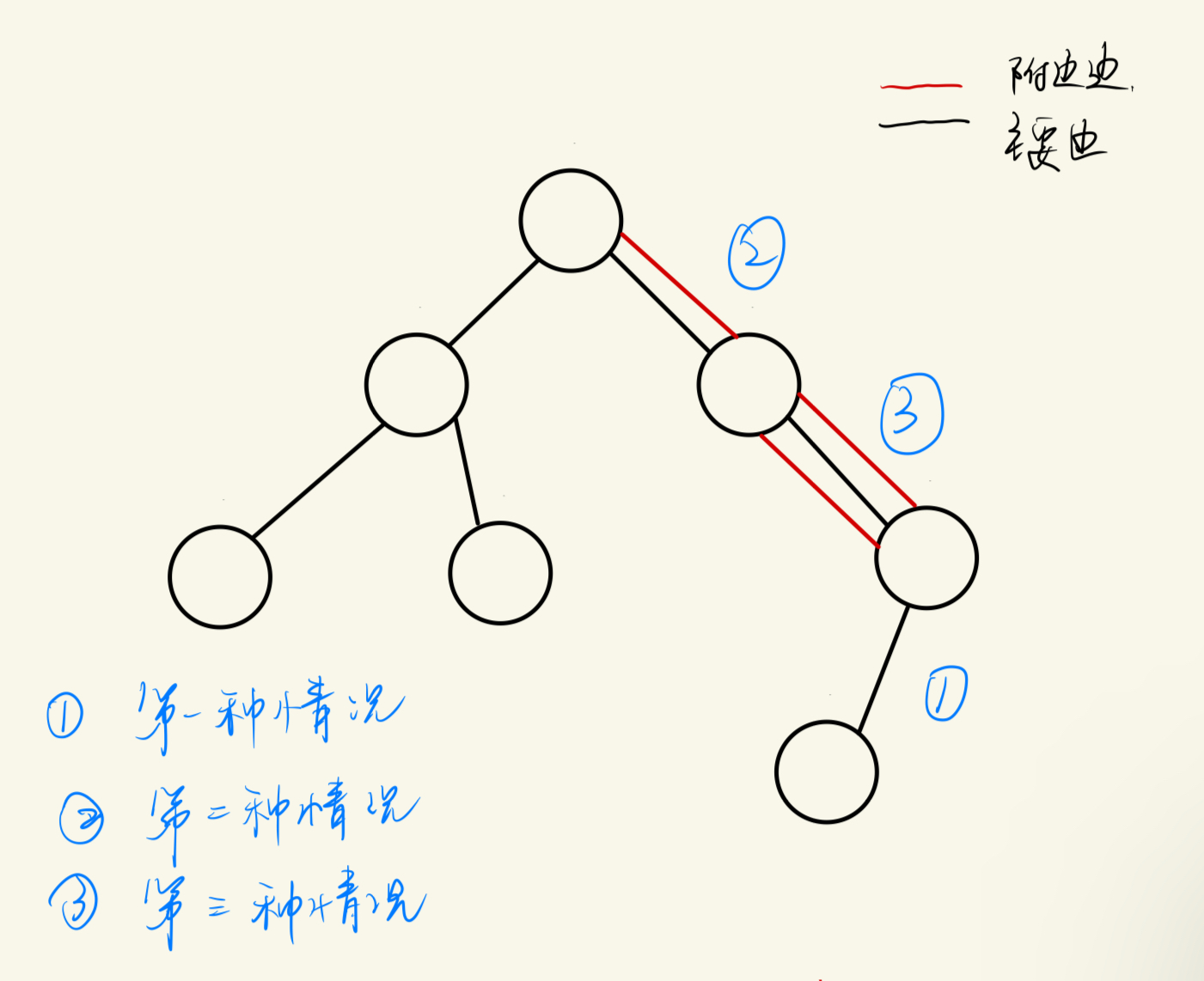
由于本来一棵树，我任意删除一条边都是可以断开树的，但是现在有了 附加边 的加入使得本来应该断开的树又被连上了，那么我们就要删除这条 连上两棵树的 附加边 ，再假设一个概念， ==覆盖== ：之前说了 附加边 会导致树上成环，那我们就可以将环上的所有 主要边 都是被这条 附加边 覆盖。

1. 第一种情况就是这条没有 附加边 覆盖这条主要边，那么这条 主要边 的贡献值就是 $k$ ，因为删除了这条 主要边 之后经已经断开这棵树， 附加边 就可以任意选择。
2. 第二种情况就是这条 主要边 被一条 附加边 覆盖，那么只要删除了这个 主要边 和 附加边 就可以将这个环分成两条链，也就分开了树，所以这条 主要边 的贡献值就是 $1$.
3. 第三种情况就是有多条边覆盖 主要边 那么我们只能删除一条显然是无法断开它的， 所以贡献值就是 $0$.

代码

// Problem: 闇の連鎖
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/description/354/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

#define inf 0x3f3f3f3f
#define pii pair<int, int>
#define lowbit(x) x&(-x)
using namespace std;
const int N = 4e5 + 10;
const int mod = 1e9 + 7;
#define int long long
const double pie = 3.1415926;

int dp[N][38];
int dep[N];
int e[N], ne[N], h[N], idx;
bool st[N];
int d[N];
int ans = 0;
int n, k;
void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }

int dfs1(int u, int fa) {
  int res = d[u];
  // cout << res << endl;
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (j != fa) {
      int s = dfs1(j, u);
      if (s == 0)
        ans += k;
      else if (s == 1)
        ans++;
      res += s;
    }
  }
  // ans = max(ans, res);
  return res;
}

void dfs(int u) {
  for (int i = 1; (1 << i) < dep[u]; i++) {
    dp[u][i] = dp[dp[u][i - 1]][i - 1];
  }
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (st[j]) continue;
    st[j] = 1;
    dep[j] = dep[u] + 1;
    dp[j][0] = u;
    dfs(j);
  }
  return;
}

int lca(int a, int b) {
  if (dep[a] < dep[b]) swap(a, b);

  int k = log2(dep[a] - dep[b]);

  for (int i = k; i >= 0; i--) {
    if (dep[dp[a][i]] >= dep[b]) a = dp[a][i];
  }
  if (a == b) return a;

  k = log2(dep[a]);
  for (int i = k; i >= 0; i--) {
    if (dp[a][i] == dp[b][i]) continue;
    a = dp[a][i];
    b = dp[b][i];
  }
  return dp[a][0];
}

void solve() {
  cin >> n >> k;
  memset(h, -1, sizeof h);
  for (int i = 1; i <= n - 1; i++) {
    int a, b;
    cin >> a >> b;
    add(a, b);
    add(b, a);
  }
  st[1] = 1;
  dfs(1);

  for (int i = 0; i < k; i++) {
    int a, b;
    cin >> a >> b;
    int p = lca(a, b);

    d[a]++, d[b]++, d[p] -= 2;
  }
  // for (int i = 1; i <= n; i++) cout << dep[i] << " \n"[i == n];
  dfs1(1, -1);
  cout << ans << endl;
}

#undef int
int main() {
  cout << fixed << setprecision(3);
  int t = 1;
  // cin >> t;
  int tt = t;
  while (t--) {
    // cout << "Case #" << tt - t << ": ";
    solve();
    // cout << endl;
  }
  return 0;
}