高斯消元

点赞+收藏过10更新

不知道大家喜不喜欢轻松的类型。

这期变的严肃一点，然后内容精炼一点吧。

一、作用

看题

我们先把方程写下来。

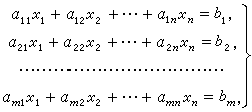
总共有$n$个方程。

要求就是：在$n^3$的时间复杂度内求解这个多元线性方程组

我们先来讨论一下解的几种情况：

$ ans \left\\{ \begin{aligned} have \\\ no \\\ \infty \\\ \end{aligned} \right. $
就是有解，一个解，无数个解的意思。

然后说一下怎么解这个方程。

要想求解的话我们需要用到初等行列变换。

没错就是线性代数。

注意这里的方程组是正方形的。

规则如下：

1. 对某一行乘以一个非0的数
2. 交换某两行
3. 把一行的若干倍加到另一行去。

对应的是：

1. 等式两边同时乘以一个相同且非0的数
2. 交换两个方程的位置
3. 把一个方程的若干倍加到另一个方程上去

我们来尝试解一下方程。

解出来的具体方法就是把方程变成下面这个样：
$$ a_{1_1}x_1 + \ldots + a_{1_n}x_n = b_1\\\ a_{2_2}x_2 + \ldots + a_{2_n}x_n = b_2\\\ \ldots x_n = b_n $$
继续解：
$$ \ldots a_{n-1_{n-1}}x_{n-1}+a_{n-1_n}x_n=b_n-1\\\ x_n = b_n $$
这样就可以都求出来了。

有矛盾：$0 != 0$——无解

有一些方程没有意义：$0=0$——无穷多组解

我们不妨试着来解一下：
$$ \begin{matrix} 1 & 2 & -1 & -6 \\\ 2 & 1 & -3 & -9 \\\ -1 & -1 & 2 & 7 \\\ \end{matrix} $$

1. 枚举每一列：$c$
2. 找到非0的一行（绝对值最大的一行） 此时找到的应该是第一列第二行的$2$。
3. 把这行交换到最上面去

$$ \begin{matrix} 2 & 1 & -1 & -9 \\\ 1 & 2 & -3 & -6 \\\ -1 & -1 & 2 & 7 \\\ \end{matrix} $$

然后把这一行的第一个数变成$1$。(同时除以第一个数)

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 1 & 2 & -1 & 6 \\\ -1 & -1 & 2 & 7 \\\ \end{matrix} $$

然后把这一列除了第一个数全部变成$0$。

第二行减去第一行，第三行加上第一行。

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1.5 & 0.5 & -1.5 \\\ 0 & -0.5 & 0.5 & 2.5 \\\ \end{matrix} $$

然后继续迭代。

注意此时第一行已经固定了，不能再动了。

第二行绝对值最大。

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1.5 & 0.5 & -1.5 \\\ 0 & -0.5 & 0.5 & 2.5 \\\ \end{matrix} $$

然后把$1.5$变成$1$。

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1 & \frac 1 3 & -1 \\\ 0 & -0.5 & 0.5 & 2.5 \\\ \end{matrix} $$

接着消成$0$。

要把第三行加上二分之一的第二行。

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1 & \frac 1 3 & -1 \\\ 0 & 0 & \frac 2 3 & 2 \\\ \end{matrix} $$
此时就变成了一个完美的阶梯型，所以有唯一解。

我们先把最后一个方程第一个数变成$1$。

也就是除以$\frac 2 3$

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1 & \frac 1 3 & -1 \\\ 0 & 0 & 1 & 3 \\\ \end{matrix} $$

得出：$x_3 = 3$

消第二个方程：

用这个方程减去第三行乘以$\frac 1 3$

$$ \begin{matrix} 1 & 0.5 & -1.5 & -4.5 \\\ 0 & 1 & 0 & -2 \\\ 0 & 0 & 1 & 3 \\\ \end{matrix} $$

得出：$x_2 = -2$

然后解第一个方程：

先减去第二个方程乘以$\frac 1 2$

再减去第三个方程乘以$1.5$

$$ \begin{matrix} 1 & 0 & 0 & 1 \\\ 0 & 1 & 0 & -2 \\\ 0 & 0 & 1 & 3 \\\ \end{matrix} $$

得出：$x_1 = 1$

然后就搞定了。

$$ x_1 + 0x_2 + 0x_3 = 1 0x_1 + x_2 + 0x_3 = -2 0x_1 + 0x_2 + x_3 = 3 $$

$$ x_1 = 1 x_2 = -2 x_3 = 3 $$

那么我们用代码实现一下。

int gauss()
{
    int c = 0, r = 0;
    for(c = 0, r = 0; c < n; c++)
    {
        int t = r;
        for(int i = r; i < n; i ++)
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        if(fabs(a[t][c]) < OP) continue;
        for(int i = c; i < n + 1; i ++) swap(a[t][i], a[r][i]);
        for(int i = n; i >= c; i --) a[r][i] /= a[r][c];
        for(int i = r + 1; i < n; i ++)
            if(fabs(a[i][c]) > OP)
                for(int j = n; j >= c; j --)
                    a[i][j] -= a[r][j] * a[i][c];
        r ++;
    }
    if(r < n)
    {
        for(int i = r; i < n; i ++)
            if(fabs(a[i][n]) > OP)
                return 2;
        return 1;
    }
    for(int i = n - 1; i >= 0; i --)
        for(int j = i + 1; j < n; j ++)
            a[i][n] -= a[j][n] * a[i][j];
    return 0;
}

好像稍微有一点吓人，这是最开始那道题的完整代码：

/*
高斯消元算法步骤
1、代谢每一列
    （1）找到这一列中绝对值最大的那一行。
    （2）把这一行换到最上面（置顶方程）
    （3）将这一行的第一个数变成1
    （4）将下面所以行的当前列消成0
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
const double OP = 1e-6;
int n;
double a[N][N];
int gauss()
{
    int c = 0, r = 0;
    for(c = 0, r = 0; c < n; c++)
    {
        int t = r;
        for(int i = r; i < n; i ++)
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        if(fabs(a[t][c]) < OP) continue;
        for(int i = c; i < n + 1; i ++) swap(a[t][i], a[r][i]);
        for(int i = n; i >= c; i --) a[r][i] /= a[r][c];
        for(int i = r + 1; i < n; i ++)
            if(fabs(a[i][c]) > OP)
                for(int j = n; j >= c; j --)
                    a[i][j] -= a[r][j] * a[i][c];
        r ++;
    }
    if(r < n)
    {
        for(int i = r; i < n; i ++)
            if(fabs(a[i][n]) > OP)
                return 2;
        return 1;
    }
    for(int i = n - 1; i >= 0; i --)
        for(int j = i + 1; j < n; j ++)
            a[i][n] -= a[j][n] * a[i][j];
    return 0;
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j <n + 1; j ++ )
            cin >> a[i][j];
    int g = gauss();
    if (g == 0)
    {
        for (int i = 0; i < n; i ++ )printf("%.2lf\n", a[i][n]);
    }
    else if (g == 1)puts("Infinite group solutions");
    else puts("No solution");
    return 0;
}

好了今天的分享就到这里了。

这是我的全部分享

bye~