快速傅里叶变换（FTT）

用途：O(nlogn) 高精度乘法

快速傅里叶变换（FFT）是一种能在$O(nlogn)$的时间内将一个多项式转换成它的点值表示的算法。

什么是点值表示

设A(x)是一个n−1次多项式，那么把n个不同的x代入，会得到n个y。这n对(x,y)唯一确定了该多项式

FFT可以用来加速多项式乘法（x=10代入）

有两个n−1次多项式A(x)和B(x)

普通的多项式乘法是$$O(n^2)$$

枚举A(x)中的每一项，分别与B(x)中的每一项相乘，得到一个新多项式C(x)

两个用点值表示的多项式相乘，复杂度$O(n)$

$C(x_i)=A(x_i)×B(x_i)$

不懂直接相乘的看附录图

新的瓶颈在于把多项式转换成点值表示的朴素算法是$O(n^2)$

把点值表示转换为多项式的朴素“插值算法”也是$O(n^2)$的

大整数乘法复杂度的瓶颈可能在多项式转换成点值表示这一步（，只要完成这一步就可以$O(n)$求答案了。

离散傅里叶变换

复数：

$z=a+bi$

$\bar{z}=a-bi $

$z\times\bar{z}=a^2+b^2$

$z=r\times(cos\theta+isin\theta)$ 其中 $r=|z|$

$\theta$ 为 $z$ 的辐角 记为 $Arg(z)$

在区间$[-π,π]$内的辐角称为 辐角主值 记为 $arg(z)$

$z$的$arg$是唯一的

$z=r(cos\theta+isin\theta)=re^{i\theta}$

复数相乘的规则：模长相乘，幅角相加

C++的STL提供了复数模板
头文件：#include <complex>
定义： complex<double> x;

傅里叶要用到的n个复数，是——把单位圆（圆心为原点、1为半径的圆）n等分，取这n个点（或点表示的向量）所表示的虚数，即分别以这n个点的横坐标为实部、纵坐标为虚部，所构成的虚数。

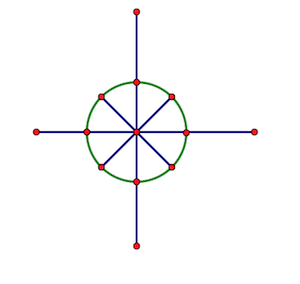
从点(1,0)开始，逆时针将这n个点从0开始编号，第k个点对应的虚数记作$ω^k_n$（根据复数相乘时模长相乘幅角相加可以看出，$ω^k_n$是$ω^1_n$的k次方，所以$ω^1_n$被称为n次单位根）。

根据每个复数的幅角，可以计算出所对应的点/向量。$ω^k_n$对应的点/向量是$(coskn2π,sinkn2π)$，也就是说这个复数是$cos\frac{k}{n}2π+isin\frac{k}{n}2π$。

傅里叶说：把n个复数$ω^0_n$,$ω^1_n\dots$,$ω^{n-1}_n$代入多项式，能得到一种特殊的点值表示，这种点值表示就叫离散傅里叶变换吧！

单位根的性质

$ω^{2k}_{2n}=ω^k_n$

$ω^{k+\frac n 2}_n=−ω^k_n$ 它们对应的点是关于原点对称的

设$(y_0,y_1,y_2,…,y_{n−1})$为多项式$A(x)=a_0+a_1x+a_2x^2+…+a_{n−1}x^{n−1}$的离散傅里叶变换。

设$B(x)=y_0+y_1x+y_2x^2+…+y_{n−1}x^{n−1}$

现在我们把上面的n个单位根的倒数

$ω^0_n,ω^{−1}_n,ω^{−2}_n,…,ω^{−(n−1)}_n$

作为 $x$ 带入 $B(x)$

得到 $(z_0,z_1,z_2,…,z_{n−1})$
$$ \begin{align} z_k&=\sum\limits^{n-1}_{i=0}y^i(w_n^{-k})^i\\ &=\sum\limits^{n-1}_{i=0}(\sum\limits^{n-1}_{j=0}a_j(w_n^i)^j)(w_n^{-k})^i\\ &=\sum\limits^{n-1}_{j=0}a_j(\sum\limits^{n-1}_{i=0}(w_n^{j-k})^i)\\ \end{align} $$
$\sum\limits^{n-1}_{i=0}(w_n^{j-k})^i$ 当$j=k$ 时 为 $n$

其余时间 等比数列求和可得$0$

namo $z_k=na_k$

namo $a_i=\frac {z_i} {n}$

结论

把多项式A(x)的离散傅里叶变换结果作为另一个多项式B(x)的系数，取单位根的倒数即$ω^0_n$,$ω^1_n\dots$,$ω^{n-1}_n$作为x代入B(x，得到的每个数再除以n，得到的是A(x)的各项系数。

快速傅里叶变换

傅里叶发明了神奇的变换，能把多项式转换成点值表示又转换回来，但仍然是暴力代入的做法，复杂度仍然是$O(n^2)$

快速傅里叶变换应运而生。它是一种分治的傅里叶变换
$$ \begin{align} A(x)=&a_0+a_1x+a_2x^2+…+a_{n−1}x^{n−1}\\ A(x)=&(a_0+a_2x^2+…+a_{n−2}x^{n−2})\\&(a_1x+a_3x^3+…+a_{n−1}x^{n−1})\\ A_1(x)=&(a_0+a_2x^+…+a_{n−2}x^{\frac {n}{2}−1})\\ A_2(x)=&(a_1+a_3x+…+a_{n−1}x^{\frac {n}{2}−1})\\ A(x)=&A_1(x^2)+xA_2(x^2)\\ \forall k<&\frac n 2 \quad x=w^k_n\\ A(w^k_n)=&A_1(w^{2k}_n)+w^k_nA_2(w^{2k}_n)\\ =&A_1(w^{k}_{\frac n 2})+w^k_nA_2(w^{k}_{\frac n 2})\\ A(w^{k+\frac n 2}_n)=&A_1(w^{2k+n}_n)+w^{k+\frac n 2}_nA_2(w^{2k+n}_n)\\ =&A_1(w^{k}_{\frac n 2}\times w^n_n)+w^{k+\frac n 2}_nA_2(w^{k}_{\frac n 2}\times w^n_n)\\ =&A_1(w^k_{\frac n 2})-w^k_nA_2(w^k_{\frac n 2}) \end{align} $$

由此便转为了分治问题

边界是$n=1$

附录