quick_sort

采用分治的思想, 不稳定

1. 确定分界点（一般取中点）
2. key 调整区间
3. 递归处理左右两段

/* 
    设两个指针 i, j 分别在左右两端
    移动 i 直至当前数大于分界点
    移动 j 直至当前数小于分界点
    交换两指针所指的数
    递归继续
*/

void quick_sort(int q[], int l, int r) {
    if (l >= r) return ;
    int x = q[l + r >> 1], i = l - 1, j = r + 1; // 先移动, 再判断
    while (i < j) {
        do i++; while (q[i] < x);
        do j--; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j); quick_sort(q, j + 1, r);
}

merge_cort

采用分治的思想, 稳定

1. 确定分界点
2. 递归排序两个区间
3. key 两个区间合并

/*  
    设两个指针分别指向两个有序区间的最小值 
    比较两指针所指数大小, 取较小者放入最终数组 
*/

void merge_sort(int q[], int l, int r) {
    if (l >= r) return ;
    int mid = l + r >> 1;
    merge_sort(q, l, mid); merge_sort(q, mid + 1, r);
    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {
        if (q[i] <= q[j]) tmp[++k] = q[i++];
        else tmp[++k] = q[j++];
    }
    while (i <= mid) tmp[++k] = q[i++];
    while (j <= r) tmp[++k] = q[j++];
    for (i = l, j = 1; i <= r; i++, j++) q[i] = tmp[j];
}

整数二分

求最大值

void bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
}

求最小值

void bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
}

浮点数二分

void bsearch_3(double x) {
    double l = 0, r = x;
    while (r - l > 1e-8) {
        double mid = (l + r) / 2;
        if (mid * mid >= x) r = mid;
        else l = mid;
    }
}

前缀和

求数组 $a$ 中 a[l] + a[l+1] + ... + a[r]

定义数组 $s$ s[i] = a[1] + a[2] + ... + a[i]

则 s[i] = s[i-1] + a[i], 易得结果为 s[r] - s[l-1]

预处理 $O(n)$, 询问 $O(1)$

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e5 + 10;

int n, m, a[N], s[N], l, r;

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]), s[i] = s[i-1] + a[i]; // 预处理
    while (m--) {
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l-1]); // 询问
    }
    return 0;
}

二维前缀和

求矩阵 $a$ 中子矩阵 a[x1][y1] + a[x1][y1+1] + ... + a[x2][y2] 中数字之和

与一维类似的, 定义矩阵 $s$ s[i][j] = a[1][1] + a[1][2] + ... + a[i][j] 的和

则 s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j], 结果为 s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]

预处理 $O(nm)$, 查询 $O(1)$

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1010;

int n, m, q, a[N][N], s[N][N], x1, y1, x2, y2;

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j]; // 预处理
    while (q -- ) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]); // 查询
    }
    return 0;
}

差分

实为前缀和的逆运算

给定数组 $a$, 规定区间 $l, r$, 使 a_l - a_r 都加上 $x$

构造 $b$ 数组, 满足 $a$ 数组为其前缀和数组, 则 $b$ 数组为 $a$ 数组的差分数组

可得 b[i] = a[i] - a[i-1]

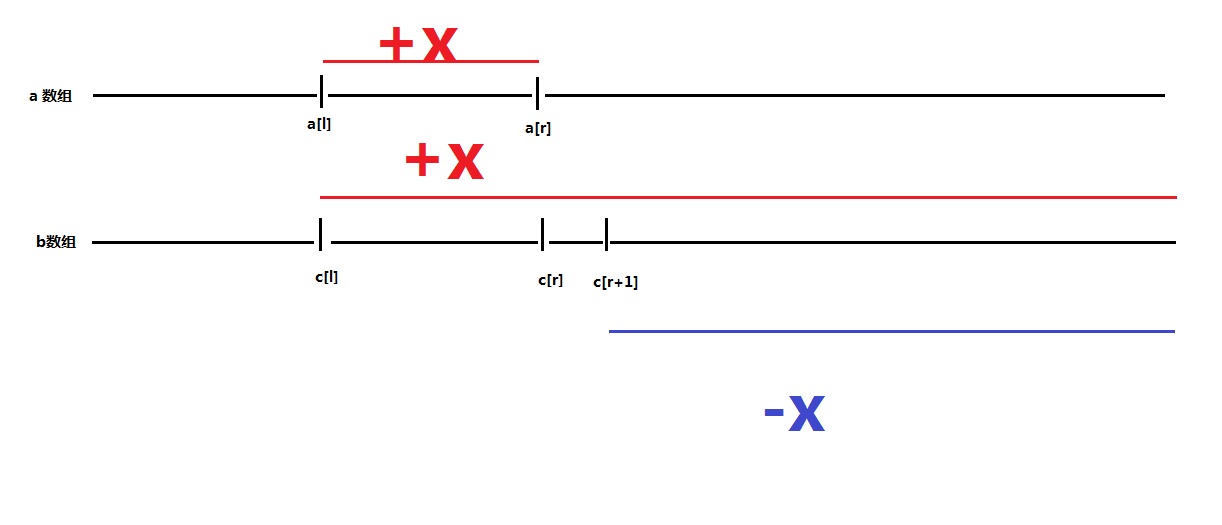
则给 $a$ 数组的一段区间加上 $x$, 可转化为给 $b$ 数组的一段区间加上 $x$

则 b[l] += x, b[r+1] -= x, 再进行前缀和求和运算, 即可求得 $a$ 数组

预处理 $O(1)$, 查询 $O(n)$

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e5 + 10;

int n, m, a[N], b[N], l, r, x;

void insert(int l, int r, int x) {
    b[l] += x, b[r+1] -= x;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= n; i++)
        insert(i, i, a[i]);
    while (m -- ) {
        scanf("%d%d%d", &l, &r, &x);
        insert(l, r, x);
    }
    for (int i = 1; i <= n; i++)
        a[i] = a[i-1] + b[i];
    for (int i = 1; i <= n; i++)
        printf("%d ", a[i]);
    return 0;
}

二维差分

同理可得, 二维差分系二维前缀和的逆运算, 原理不再赘述

b[x1][y1] += x, b[x2+1][y1] -= x, b[x1][y2+1] -= x, b[x2+1][y2+1] += x;

预处理 $O(1)$, 查询 $O(nm)$

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1010;

int n, m, q, a[N][N], b[N][N], x1, y1, x2, y2, x;

void insert(int x1, int y1, int x2, int y2, int x) {
    b[x1][y1] += x, b[x2+1][y1] -= x, b[x1][y2+1] -= x, b[x2+1][y2+1] += x;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);
    while (q -- ) {
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &x);
        insert(x1, y1, x2, y2, x);
    }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) 
            printf("%d ", a[i][j]);
        printf("\n");
    }
    return 0;
}