线段树可以在 O(log N) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树的操作

1. pushup(u)
2. build() 将一段区间初始化成线段树
3. modify() 修改单点或区间
4. query() 查询

线段树原理

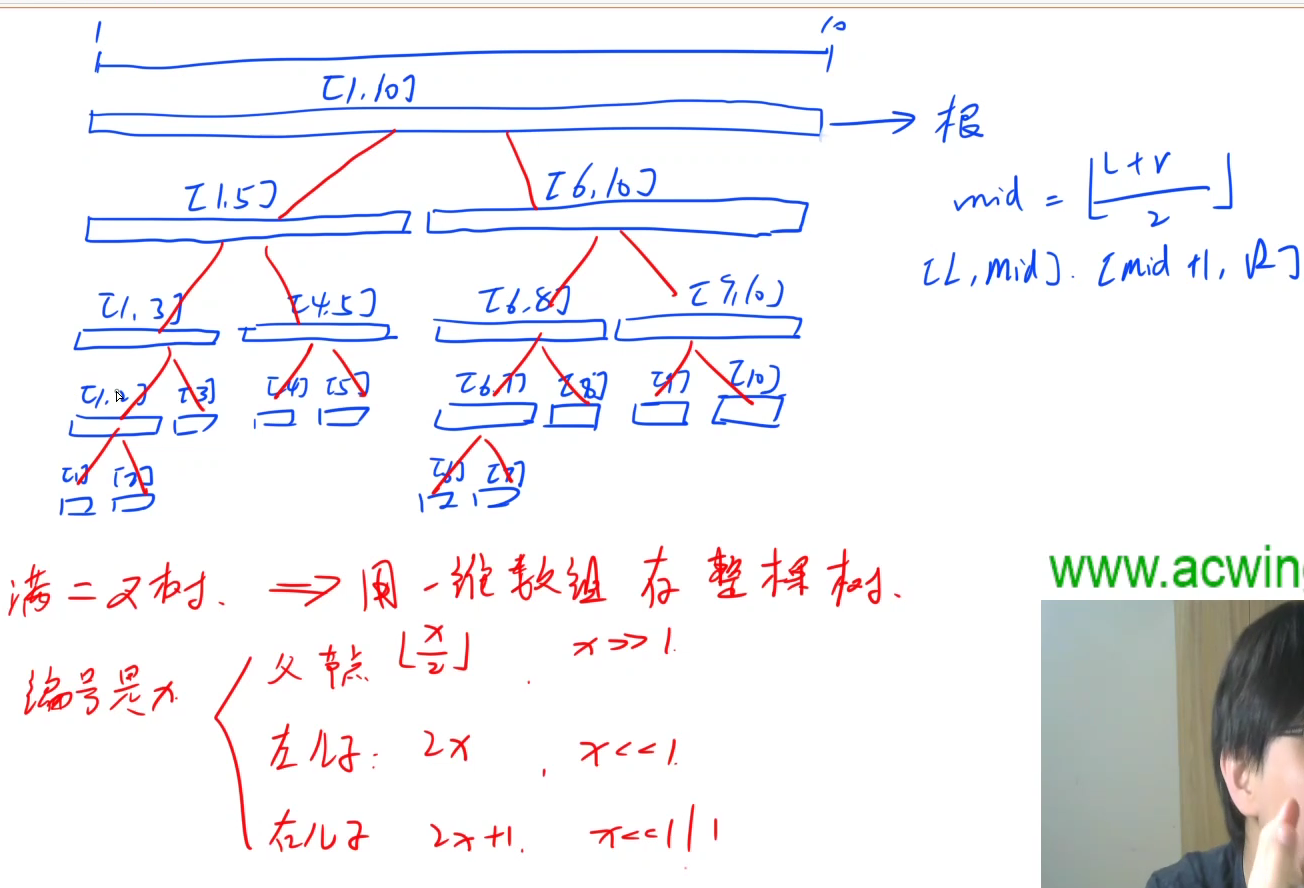
开空间需要开4*n

// pushup 用子节点更新父节点
void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v); // 根据具体询问，更改pushup内容
}

建树

build(int u, int l, int r)
{
    tr[u].l = l, tr[u].r = r;
    if (l == r) return ;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

查询

假设查询区间是[l, r]，树中的节点范围是 [$T_l$, $T_r$]

1. [$T_l$, $T_r$] $\subset$ [l, r] ，直接返回

2. [$T_l$, $T_r$] $\cap$ [l, r] $\neq$ $\varnothing$

3. [$T_l$, $T_r$] $\cap$ [l, r] = $\varnothing$ (不存在)

第2种情况又可以分为3类

• $T_l$ $\leq$ l $\leq$ $T_r$ $\leq$ r

  m = ($T_l$ + $T_r$) / 2
  l > m 递归右边
  l $\leq$ m 递归左、递归右

• l $\leq$ $T_l$ $\leq$ r $\leq$ $T_r$

  与第一种情况类似

• [l, r] $\subset$ [$T_l$, $T_r$]

  r $\leq$ m, 只递归左边
  l > m，只递归右边
  其他 递归左边、递归右边

node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);
        else if (l > mid) return query(u << 1 | 1, l, r);
        else
        {
            auto left = query(u << 1, l, r);
            auto right = query(u << 1 | 1, l, r);
            node res;
            pushup(res, left, right);
            return res;
        }
    }
}

修改和查询操作类似

// 单点修改
void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v; // 修改，根据具体询问进行修改
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

一般涉及单点修改、区间查询的线段树问题，可以不用懒标记来做，只用pushup进行维护
区间修改 需要用pushdown(懒标记)

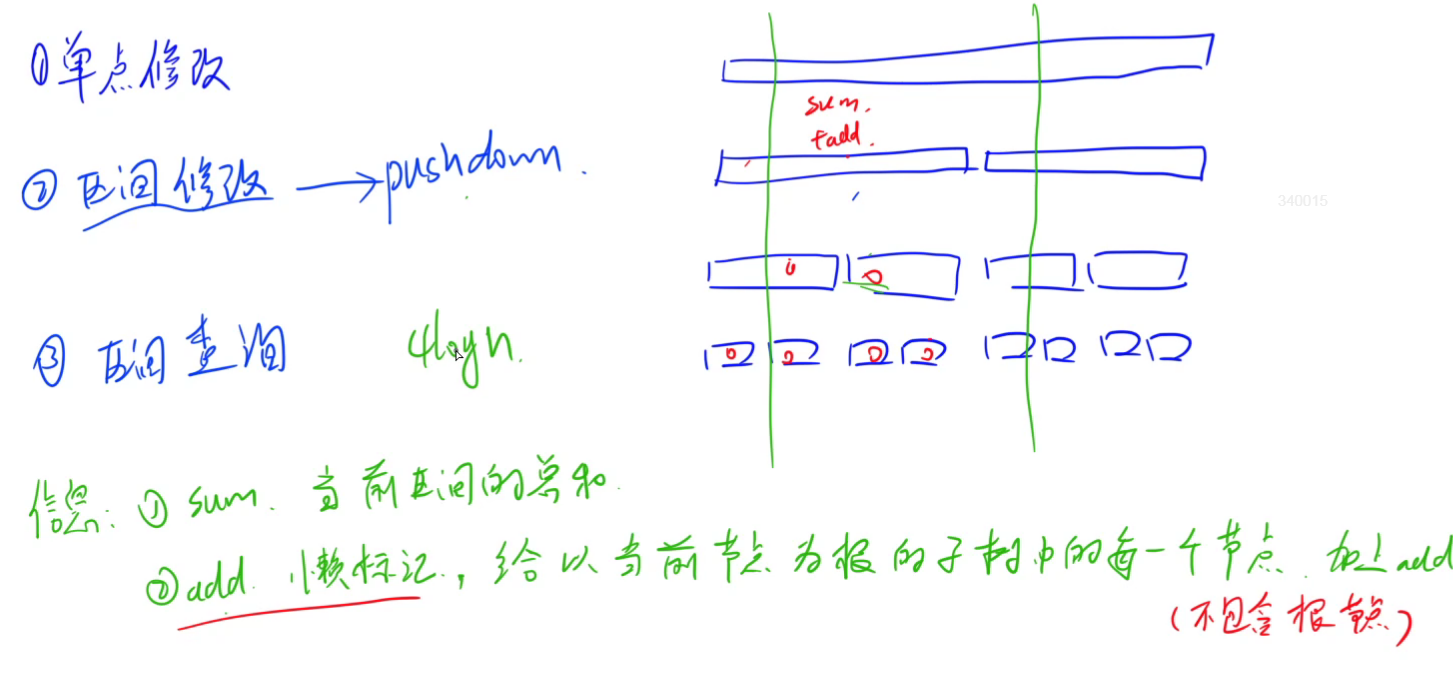
// pushdown，将懒标记由父节点向子节点传递，修改区间值
left.add += root.add;
left.sum += (left.r - left.l + 1) * root.add;
right.add += root.add;
right.sum += (right.r - right.r + 1) * root.add;
root.add = 0;