算法模板数学

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

算法模板数学

作者：

zyyyds , 2024-04-02 20:39:45 , 所有人可见 , 阅读 12

0

1

求一个数的因子与质因子

求因子
Code：

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
LL n;
vector<LL> v;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    cin >> n;
    for(int i = 1; i <= n / i; i ++)
    {
        if(n % i) continue;
        v.push_back(i);
        if(i != n / i) v.push_back(n / i); 
    }
    sort(v.begin(), v.end());
    for(auto &x : v) cout << x << " ";
    return 0; 
}

质因子：

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
LL n;
vector<LL> v;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    cin >> n;
    for(int i = 2; i <= n / i; i ++)
    {
        if(n % i) continue;
        v.push_back(i);
        while(n % i == 0) n /= i; 
    }
    if(n > 1) v.push_back(n);
    sort(v.begin(), v.end());

    for(auto &x : v) cout << x << " ";
    return 0; 
}

埃氏筛法

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e6 + 10;
int n;
vector<int> prime;
bool st[N];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    cin >> n;
    st[0] = st[1] = true;
    for(int i = 1; i <= n; i ++)
     if(!st[i])
     {
        prime.push_back(i);
        for(int j = 2 * i; j <= n; j += i) 
         st[j] = true;
     }
    for(auto &x : prime) cout << x << ' '; 
    return 0; 
}

最小公倍数gcd和最大公约数lcm

Code

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e6 + 10;

LL gcd(LL x, LL y)
{
    if(!y) return x;
    else return gcd(y, x % y);
} 

LL lcm(LL x, LL y)
{
    return x / gcd(x, y) * y;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    int T;
    cin >> T;
    while(T --)
    {
    LL a, b;
    cin >> a >> b;
    cout << gcd(a, b) << " " << lcm(a, b) << endl;
    }
    return 0; 
}

快速幂

Code

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e6 + 10;
LL qmi(LL a, LL b, LL mod)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) 
        {
            res = res * a % mod;
        }
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    int T;
    cin >> T;
    while(T --)
    {
     LL a, b, mod;
     cin >> a >> b >> mod;
     cout << qmi(a, b, mod) << endl;
    }
    return 0; 
}

乘法逆元

Code

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 2e6 + 10, MOD = 998244353;
//乘法逆元，在mod某个数p的意义下，除以这个数等于乘以这个数的逆元
//费马小定理：a在mod数p下的逆元就是a的p-2次方 
LL qmi(LL a, LL b, LL mod)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) 
        {
            res = res * a % mod;
        }
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

LL inv(LL t, LL MOD) //求逆元函数 
{
    return qmi(t, MOD - 2, MOD);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr); 
    int T;
    cin >> T;
    while(T --)
    {
      LL a, b, c, q;
      cin >> a >> b >> c >> q;
      while(q --)
      {
         LL x;
         cin >> x;
         cout << (a * x % MOD + b) % MOD * inv(c * x % MOD, MOD) % MOD << endl;
      } 
    }
    return 0; 
}

康托展开

求解问题：康托展开属于组合数学中的一个知识点。用于求出一个排列在全排列中的排名。
详解参考链接：康托展开详解

暴力代码 O(n^2)

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10, MOD = 998244353;

LL fac[N];
LL a[N];
void init()
{
    fac[0] = 1;
    for(int i = 1; i < N; i ++)
     {
        fac[i] = (fac[i - 1] * i) % MOD;
     }
}
int n;
LL cantor(LL a[])
{
    LL res = 0;

    for(int i = 1; i <= n; i ++)
    {
        int s = 0;
        for(int j = i; j <= n; j ++)
        {
            if(a[j] < a[i]) s ++;
        }

        res = (res + (fac[n - i] * s) % MOD) % MOD;
    }
    return res + 1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    init();
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    cout << cantor(a) << endl;  

    return 0;

}

树状数组优化代码 O(nlogn)

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10, MOD = 998244353;

LL fac[N];
LL a[N];
LL t[N];
int n;
int lowbit(int x)
{
    return x & -x;
}

void add(int x, LL w)
{
    for(int i = x; i <= n; i += lowbit(i)) t[i] += w;
}

LL query(int x)
{
    LL s = 0;
    for(int i = x; i > 0; i -= lowbit(i))
    s += t[i];

    return s; 
}
void init()
{
    fac[0] = 1;
    for(int i = 1; i < N; i ++)
     {
        fac[i] = (fac[i - 1] * i) % MOD;
     }
}

LL cantor(LL a[])
{
    LL res = 0;

    for(int i = 1; i <= n; i ++)
    {
        LL s = 0;
        s = query(a[i]) - 1;
        add(a[i], -1);
        res = (res + (fac[n - i] * s) % MOD) % MOD;
    }
    return res + 1;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    init();
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];

    for(int i = 1; i <= n; i ++) add(i, 1);

    cout << cantor(a) << endl;  

    return 0;
}

逆康托展开

康托展开是一个全排列到一个自然数的双射，因此是可逆的。
逆康托展开相当于康托展开逆过来，也就是可以求出某个数某个排名的排列。
逆康托展开算法详解：逆康托展开
Code：

#include<bits/stdc++.h>
#define endl '\n' 
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e6 + 10, MOD = 998244353;
int n; 
LL num;
LL fac[N];
bool flag[N];
void init()
{
     fac[0] = 1;
     for(int i = 1; i < N; i ++) 
     {
        fac[i] = (fac[i - 1] * i) % MOD;
     }

} 

void decantor(LL num)
{
    num --;
    int j;
    for(int i = 1; i <= n; i ++) flag[i] = false;
    for(int i = 1; i <= n; i ++)
    {
        int cnt = num / fac[n - i];
        for(j = 1; j <= n; j ++)
        {
            if(!flag[j])
            {
               if(!cnt) break;
               cnt --;  
            } 
        }
        cout << j << " ";
        flag[j] = true;
        num %= fac[n - i];
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    init();
    cin >> n >> num;
    decantor(num);
    return 0;

}

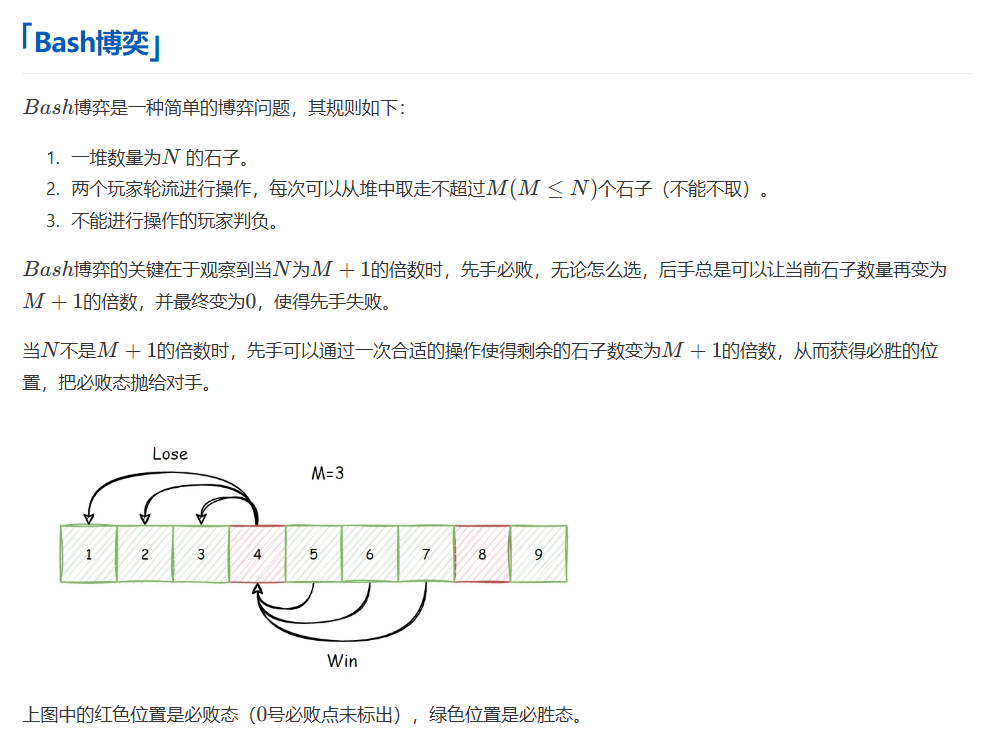
Bash博弈

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e4 + 10, MOD = 1e9 + 7;

void solve()
{
    int n, m;

    cin >> n >> m;

    if(n % (m + 1) == 0)
    {
        cout << "NO" << endl;
    }
    else cout << "YES" << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T;
     cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

Nim博弈

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 1e4 + 10, MOD = 1e9 + 7;

void solve()
{
    int ans = 0;
    int n;

    cin >> n;

    for(int i = 1; i <= n; i ++)
    {
        int x;
        cin >> x;
        ans ^= x;
    }

    if(ans == 0) cout << "NO" << endl;
    else cout << "YES" << endl;
} 

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T;
     cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

集合Nim游戏与SG函数

原理解析

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 110, MOD = 1e9 + 7, M = 1e4 + 10;
int k, n;
int a[N];

int sg[M];
//记忆化搜索求sg 
int getsg(int x)
{
    if(sg[x] != -1) return sg[x];

    unordered_set<int> s;

    for(int i = 0; i < k; i ++)
    {
        if(x >= a[i])
        {
            s.insert(getsg(x - a[i]));
        }
    }

    for(int i = 0;; i ++) if(s.count(i) == 0) return sg[x] = i;
}
void solve()
{
   memset(sg, -1, sizeof sg);

   cin >> k;

   for(int i = 0; i < k; i ++) cin >> a[i];

   cin >> n;

   int ans = 0;
   for(int i = 0; i < n; i ++)
   {
       int x;
       cin >> x;
       ans ^= getsg(x);
   }   

   if(ans) cout << "Yes" << endl;
   else cout << "No" << endl;
} 

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     //cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

台阶Nim游戏

原理解析

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 110, MOD = 1e9 + 7, M = 1e4 + 10;

int n;

void solve()
{
    cin >> n;

    int ans = 0;

    for(int i = 1; i <= n; i ++)
    {
         int x;
         cin >> x;
         if(i % 2) ans ^= x;    
    }   

    if(ans) cout << "Yes" << endl;
    else cout << "No" << endl;
} 

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     //cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

拆分Nim游戏

原理解析

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

const int N = 110, MOD = 1e9 + 7, M = 1e4 + 10;

int n;
int sg[N];

int getsg(int x)
{
    if(sg[x] != -1) return sg[x];

    unordered_set<int> s;
    for(int i = 0; i < x; i ++)
    {
        for(int j = 0; j <= i; j ++)
        {
            s.insert(getsg(i) ^ getsg(j));
        }
    }

    for(int i = 0;; i ++) if(s.count(i) == 0) return sg[x] = i;
}

void solve()
{
   memset(sg, -1, sizeof sg);
   cin >> n;
   int ans = 0;
   for(int i = 1; i <= n; i ++)
   {
      int x;
      cin >> x;
      ans ^= getsg(x);  
   }   

   if(ans) cout << "Yes" << endl;
   else cout << "No" << endl;
} 

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
     int T = 1;
     //cin >> T;
     while(T --)
     {
        solve();    
     }   
    return 0; 
}

0 评论

App 内打开