记忆化搜索
最大食物链计数
题目背景
你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是重复数了几条或漏掉了几条。于是她来就来求助你,然而你也不会啊!写一个程序来帮帮她吧。
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 $1$ 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 $80112002$ 的结果。
输入格式
第一行,两个正整数 $n、m$,表示生物种类 $n$ 和吃与被吃的关系数 $m$。
接下来 $m$ 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 $80112002$ 的结果。
样例 #1
样例输入 #1
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
样例输出 #1
5
提示
各测试点满足以下约定:
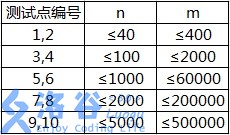
【补充说明】
数据中不会出现环,满足生物学的要求。(感谢 @AKEE )
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=1000010;
int e[N],en[N],w[N],idx,h[N];
bool st[N];
int n,m;
int f[N];
bool win[N],lose[N];
int mod=80112002;
void add(int a,int b)
{
e[idx]=b;en[idx]=h[a],h[a]=idx++;
}
int dfs(int u)
{
int num=0;
if(!win[u]) return 1;
if (f[u]) return f[u];
for (int i=h[u];i!=-1;i=en[i])
{
int j=e[i];
num=(num+dfs(j))%mod;
}
return f[u]=num;
}
int main ()
{
memset(h,-1,sizeof h);
cin >>n>>m;
while (m--)
{
int a,b;
cin >>a>>b;
win[b]=true;
lose[a]=true;
add(b,a);
}
int res=0;
for (int i=1;i<=n;i++)
{
if (!lose[i])
res=(res+dfs(i))%mod;
}
cout <<res;
return 0;
}
[SHOI2002] 滑雪
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 $24-17-16-1$(从 $24$ 开始,在 $1$ 结束)。当然 $25$-$24$-$23$-$\ldots$-$3$-$2$-$1$ 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 $R$ 和列数 $C$。下面是 $R$ 行,每行有 $C$ 个数,代表高度(两个数字之间用 $1$ 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
样例 #1
样例输入 #1
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
样例输出 #1
25
提示
对于 $100\%$ 的数据,$1\leq R,C\leq 100$。
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N][N];
int g[N][N];
int r,c;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int dp(int x,int y)
{
if (f[x][y]) return f[x][y];
f[x][y]=1;
for (int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if (a>=1&&b>=1&&a<=r&&b<=c&&g[a][b]<g[x][y])
{
f[x][y]=max(f[x][y],dp(a,b)+1);
}
}
return f[x][y];
}
int main ()
{
ios::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
cin >>r>>c;
for (int i=1;i<=r;i++)
for (int j=1;j<=c;j++)
cin >>g[i][j];
int maxx=-1;
for (int i=1;i<=r;i++)
for (int j=1;j<=c;j++)
{
maxx=max(dp(i,j),maxx);
}
cout <<maxx;
}

