前言

省选前有次模拟赛，某道计算几何，我一眼就秒了，直接鉴定为模拟退火加几何计算。
可是几何我不会，模拟退火板子也忘了……
最后只拿了三角函数那 10pts，甚至三角函数是考场现学。
没错，就是我的程序算出面积为负数角度上万的那个 b 玩意儿，被 AcWing 各路网友喷死了。

模拟退火

能试着解决计算几何、贪心、最优化（如 DP）等问题。
相对于纯随机化算法有更大概率获得答案。
当想不出正解的时候可以尝试用它骗分。

首先考虑直接随机化，看这个点的函数值。一般来说一个问题，它的函数空间有一定性质。它的函数图像一般具有一定的连续性，不是纯随机的。
例如对于某一个区间，它的左右邻域的函数值一般不会差太多，通过此性质对随机化进行优化，得到模拟退火，是一种启发式的随机化算法。

模拟退火是一个物理过程。
首先建立一个温度（步长）的概念。每次随机的时候从当前点向周围的区域内随机。
随着温度降低，步长也缩小，跳跃的随机区间也缩小。
对于温度，需要设定初始温度和终止温度，以及衰减系数 $x$。每次降温 $T = Tx$，$x$ 需要自己调整，取接近 $1$ 的小数。越接近 $1$ 衰减越慢，找到最优解的概率也越大。（指数级别衰减）

每一次在当前迭代区间中，随机选择一个点，并计算其函数值（答案）。比较新点函数值于当前最优解。
例如求全局最小值，则：

1. 新点更小，则当前点一定不是最低点，则跳到新点。
2. 新点更大，则以一定概率跳过去。因为中间可能有一个峰值阻隔，容易收敛到局部最小值。
   • 代码中的 exp(-res / t) > rd(0, 1) 就刚好实现了这两种判定。（十分玄学）

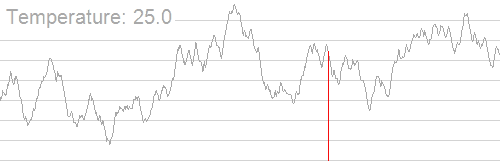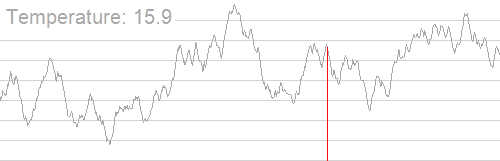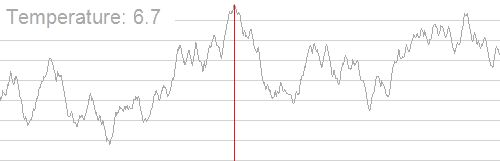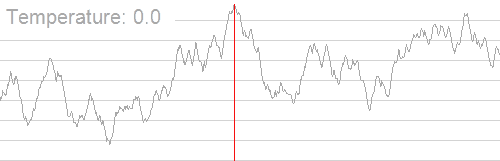
盗用借鉴一下 OI-Wiki 的图。

注意到模拟退火的运行时间较为随机，可以用卡时的方式保证不会超时。
例如：while (clock() < 0.8s)。

如果不想卡时，用调试温度系数的方法也可以。特别是衰减系数。

例题1 AcWing 3167. 星星还是树

简述题意：在二维平面找一个点，使得它到平面上 $n$ 个点总距离和最小，求最小距离和。

#include <bits/stdc++.h>
using namespace std;

const int N = 115;
const double M = 10000, eps = 1e-4;
int n;
pair<double, double> a[N];

double ans;

double rd(double l, double r) {
    return (double)rand() / RAND_MAX * (r - l) + l;
}

double dist(pair<double, double> a, pair<double, double> b) {
    double x = a.first - b.first, y = a.second - b.second;
    return sqrt(x * x + y * y);
}

double get(pair<double, double> p) {
    double res = 0;
    for (int i = 1; i <= n; i++) res += dist(p, a[i]);
    ans = min(ans, res);
    return res;
}

void solve() {
    pair<double, double> now = make_pair(rd(0, M), rd(0, M));
    for (double t = M; t > eps; t *= 0.99) {
        double x = now.first, y = now.second;
        pair<double, double> nxt = make_pair(rd(x - t, x + t), rd(y - t, y + t));
        double res = get(nxt) - get(now);
        if (exp(-res / t) > rd(0, 1)) now = nxt;
    }
}

int main() {
    srand(time(0));
    scanf("%d", &n); ans = 1e9;
    for (int i = 1; i <= n; i++) scanf("%lf%lf", &a[i].first, &a[i].second);

    for (int T = 1; T <= 100; T++) solve();

    printf("%.0lf", ans);
    return 0;
}

例题2 AcWing 2424.保龄球

对于所有排列，有一种常见的寻找周围排列的方式：随机交换两个位置。

#include <bits/stdc++.h>
#define PII pair<int, int>
using namespace std;
const int N = 55;

int n, m;
PII a[N];
int ans = 0;

int get() {
    int res = 0;
    for (int i = 1; i <= m; i++) {
        res += a[i].first + a[i].second;
        if (i <= n) {
            if (a[i].first == 10) res += a[i + 1].first + a[i + 1].second;
            else if (a[i].first + a[i].second == 10) res += a[i + 1].first;
        }
    }
    ans = max(ans, res);
    return res;
}

void solve() {
    for (double T = 1e4; T > 1e-4; T *= 0.99) {
        int x = (rand() % m) + 1, y = (rand() % m) + 1;
        int pre = get();
        swap(a[x], a[y]);
        if (n + (a[n].first == 10) == m) {
            int nxt = get();
            double delta = nxt - pre;
            if (!(exp(delta / T) > (double)rand() / RAND_MAX)) swap(a[x], a[y]);
        } else swap(a[x], a[y]);
    }
}

int main() {
    srand(time(0));
    scanf("%d", &n); m = n;
    for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].first, &a[i].second);
    if (a[n].first == 10) scanf("%d%d", &a[n + 1].first, &a[n + 1].second), m++;
    while ((double)clock() / CLOCKS_PER_SEC < 0.8) solve();
    printf("%d\n", ans);
    return 0;
}