题面:
环形石子合并
环形石子合并:f[l][r] = f[l][k] + f[k + 1][r] + s[r] - s[l - 1]
环形石子合并:
初始状态:f[l][r] = 0 (len == 1) 原因:当区间长度为1的时候无法合并
目标状态:f[1][n]
原因:我们会把区间[L, R]划分成[L, K]和[K + 1, R]
因为同一个石子只能出现在一个石碓中,因此分段点k的区间应该是[l, r - 1]
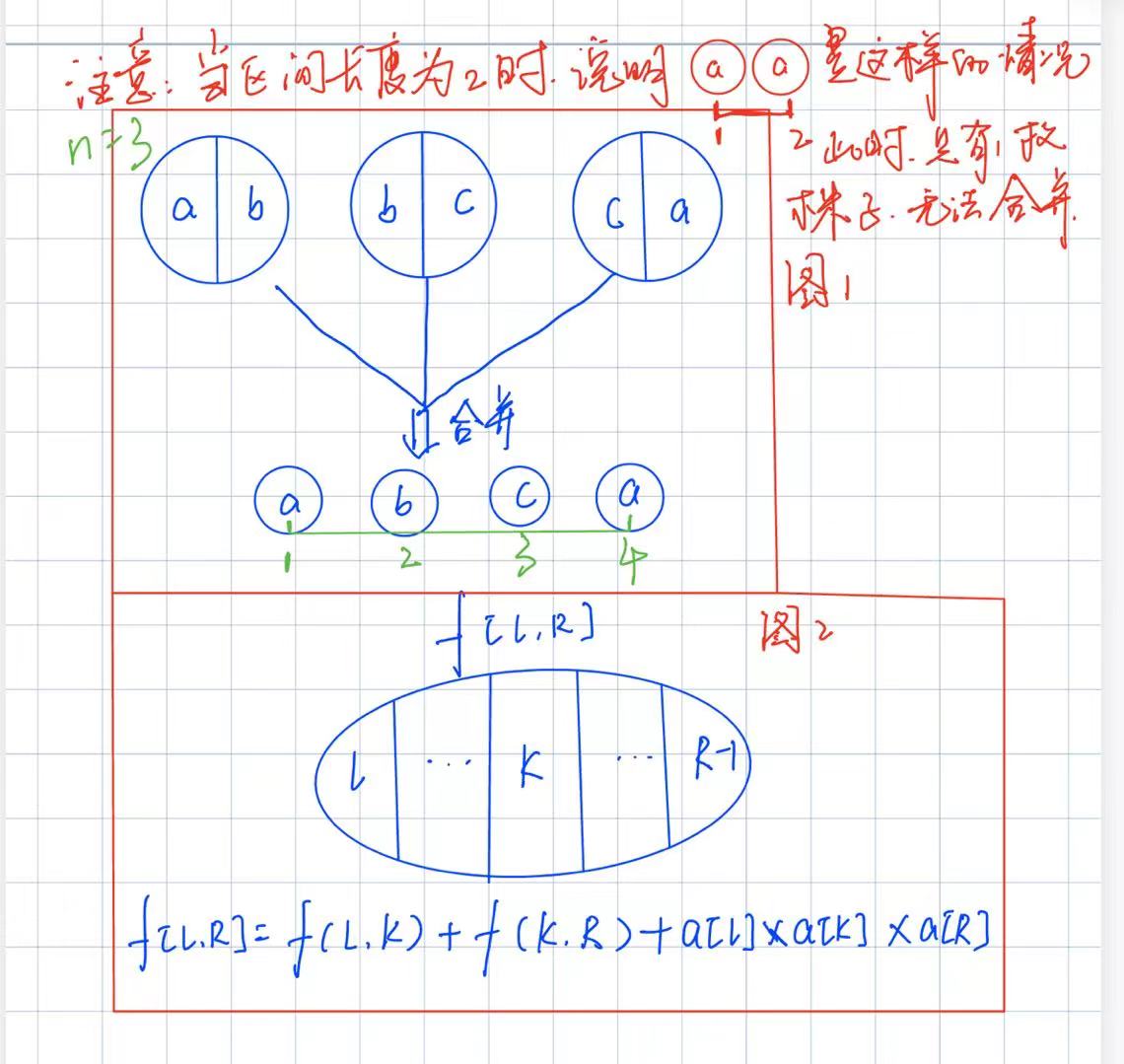
能量项链:f[l][r] = f[l][k] + f[k][r] + s[r] - s[l - 1]
初始状态:f[l][r] = 0 (len == 2)
目标状态:f[1][1 + n]
原因:我们会把区间[L, R]划分成[L, K]和[K, R]
合并珠子(石子)的时候我们会把左侧石碓的右端点和右侧石碓的左端点合并起来也就是同一颗珠子可以在不同的两个石碓里面
f[l][r + i]是因为根据题目举的例子
(2,3)(3,5)(5,10)(10,2)(2,3)(3,5)(5,10)(10,2)
假设我们随意合并一下(权值不是最大),那么第一步合并 1 2 珠子,变成 (2,5)(5,10)(10,2)(2,5)(5,10)(10,2)第二步合并当前的 1 2 珠子,变成(2,10)(10,2)(2,10)(10,2)再次合并当前的 1 2 珠子,变成 (2,2)所以此时我们也就能发现,必然有一颗珠子在合并完之后头尾标记是相同的,所以我们合并完所有珠子(x + n - 1)后,其实是合并到了第n + x个元素(注意此时区间长度的最大值是
n + 1)
其次我们应该考虑划分集合的最后一个不同点:
找到分段点k(表示第L颗珠子的尾标记,第R - 1颗珠子的头标记)因此K的范围只能是[L + 1, R - 1]
具体看下图