写在开头
- 动态规划问题的时间复杂度一般是O(状态数量*状态转移的计算量)
- 遇到涉及i-1的下标问题,一般下标从1开始可以减少越界风险
- 集合属性有三种:集合中最大值,集合中最小值,集合中元素数量
- 求最大值和最小值的,分成的子问题可以有重复;求元素数量的,分成的子问题不能有重叠
- 动态规划问题求方案:将转移状态记录下来
- 循环写法只比递归写法(记忆化搜索)快大约一个常数,但dp问题一般不卡常数
背包问题
01背包问题
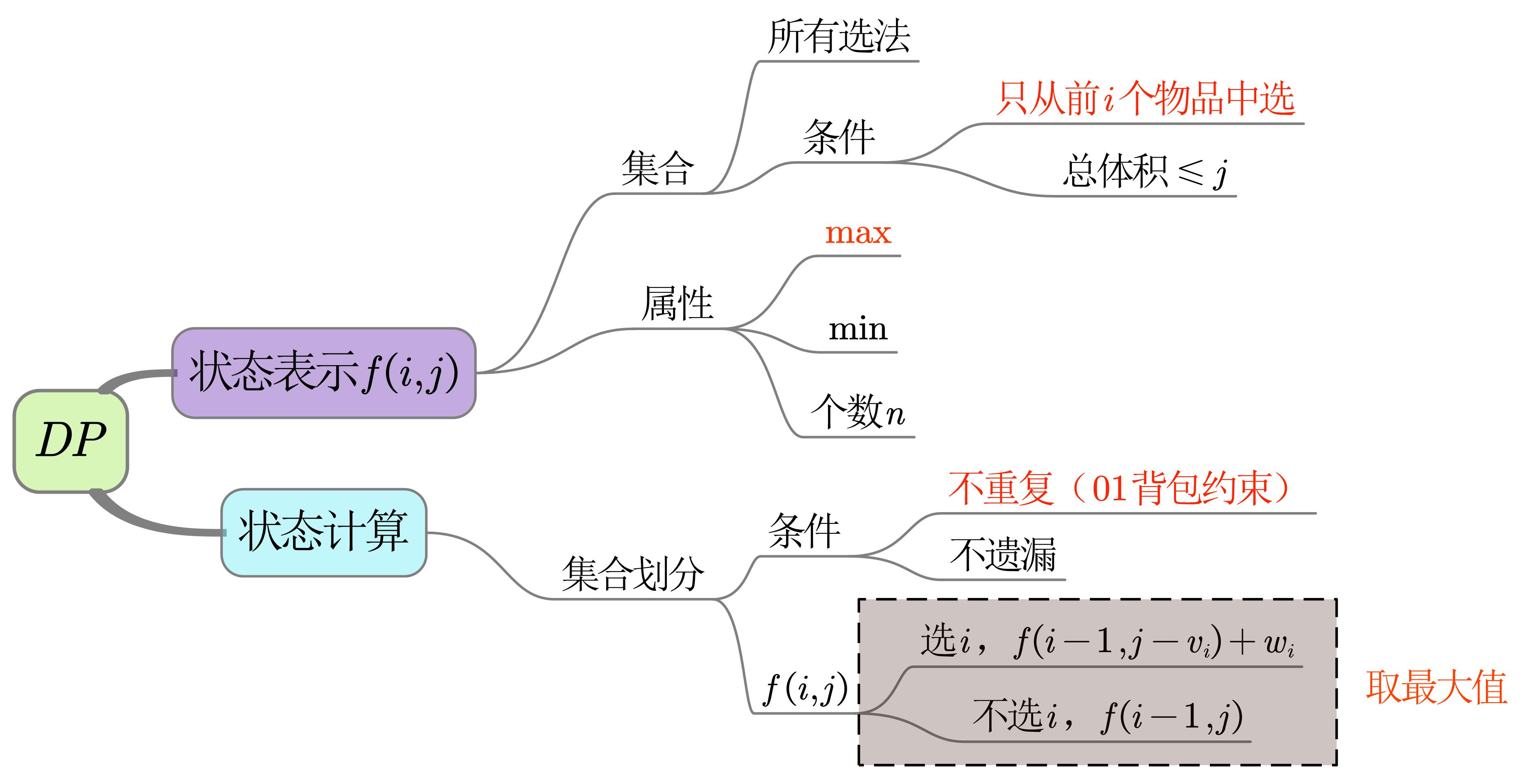
$n$个物品,每个物品的体积是$v_i$,价值是$w_i$,背包的容量是$m$
若每个物品最多只能装一个,且不能超过背包容量,则背包的最大价值是多少?
模板
int n; // 物品总数
int m; // 背包容量
int v[N]; // 重量
int w[N]; // 价值
// ---------------二维形式---------------
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
if(j < v[i]) f[i][j] = f[i-1][j]; // 当前重量装不进,价值等于前i-1个物品
else f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i]); // 能装,需判断
cout << f[n][m];
// ---------------一维形式---------------
int f[M]; // f[j]表示背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = m; j >= v[i]; --j)
f[j] = max(f[j], f[j - v[i]] + w[i]); // 注意是倒序,否则出现写后读错误
cout << f[m]; // 注意是m不是n
说明
- 注意
f[i][j]的含义:在考虑前i个物品后,背包容量为j条件下的最大价值。而不是表示选了i个物品的最大价值,实际上选择的物品数<=i。f[j]表示背包容量为j条件下的最大价值 - 二维压缩成一维,实际上是寻找避开写后读错误的方法
f[i][j]始终只用上一行的数据f[i-1][...]更新(迭代更新的基础,如果还需用上上行数据则不可压缩)f[i][j]始终用靠左边的数据f[i-1][<=j]更新(决定了只能倒序更新)
- 显然$i=0$时,$f(i, j)=0$,而初始化时自动赋予$0$,故不必但单独处理第
0行
完全背包问题
每个物品可以取任意个
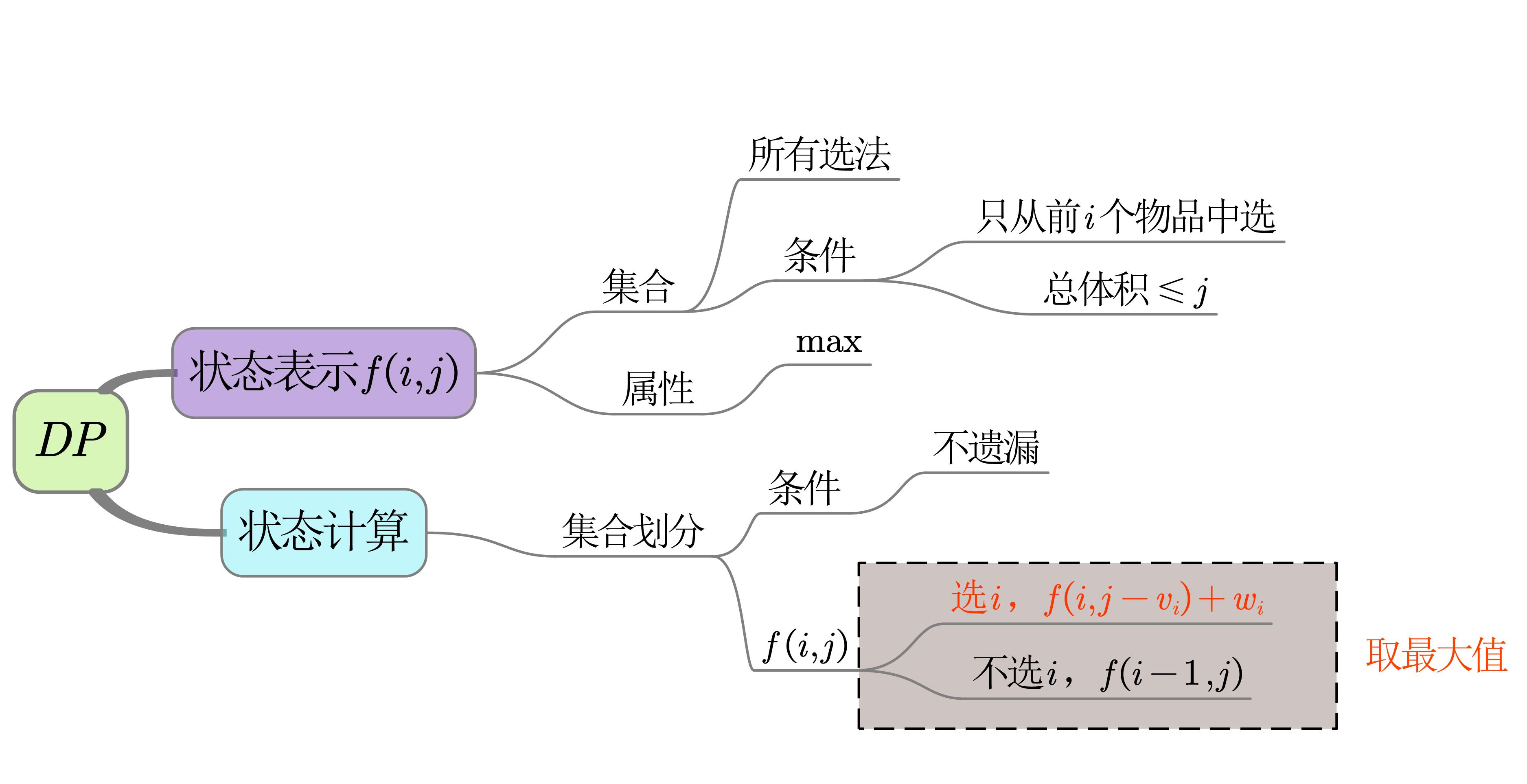
假设背包容量为$j$时,最多可装入$k$个物品$i$,则有
$$ f\left( i,j \right) =\max \left\{ f\left( i-1,j \right) , f\left( i-1,j-v_i \right) +w_i, f\left( i-1,j-2v_i \right) +2w_i,\cdots ,f\left( i-1,j-kv_i \right) +kw_i \right\} $$
考虑
$$
f\left( i,j-v_i \right) =\max \left\{ f\left( i-1,j-v_i \right) , f\left( i-1,j-2v_i \right) +w_i, f\left( i-1,j-3v_i \right) +2w_i,\cdots ,f\left( i-1,j-kv_i \right) +\left( k-1 \right) w_i \right\}
$$
上式变形得
$$
f\left( i,j-v_i \right) +w_i=\max \left\{ f\left( i-1,j-v_i \right) +w, f\left( i-1,j-2v_i \right) +2w_i, f\left( i-1,j-3v_i \right) +3w_i,\cdots ,f\left( i-1,j-kv_i \right) +kw_i \right\}
$$
综上可得
$$
f\left( i,j \right) =\max \left\{ f\left( i-1,j \right) ,f\left( i,j-v_i \right) +w_i \right\}
$$
这样就得优化后的迭代公式,和01背包问题非常相似,但后者用的是$f\left( i-1,j-v_i \right) +w_i$
模板
int n; // 物品总数
int m; // 背包容量
int v[N]; // 重量
int w[N]; // 价值
// ---------------二维形式---------------
// 未优化 (O(n*v^2)
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
// 已优化
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
if(j < v[i]) f[i][j] = f[i-1][j]; // 当前重量装不进,价值等于前i-1个物品
else f[i][j] = max(f[i-1][j], f[i][j-v[i]] + w[i]); // 能装,需判断
cout << f[n][m];
// ---------------一维形式---------------
int f[M]; // f[j]表示背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i)
for(int j = v[i]; j <= m; ++j)
f[j] = max(f[j], f[j - v[i]] + w[i]); // 注意是正序,这与完全背包的状态转移方程一致
cout << f[m]; // 注意是m不是n
说明
- 形式上和01背包差不多,在二维数组表示下,主要差别在
- 在选择第
i物品时,用的是f[i][j-v]+w,而不是f[i-1][j-v]+w - 上述条件决定了在每次迭代时,必须正向遍历,而不是反向遍历
- 在选择第
- 在一维数组表示下,主要差别只表现为迭代的顺序(正向或反向)
- 在一维数组表示下,01背包只能反向是因为它主要用到上一行的数据来更新当前行数据,如果正向遍历,则会修改上一行的数据,出现写后读错误;完全背包只能正向是因为它需要用到当前行的数据更新,如果反向遍历,使用的是上一行的数据,则不符合公式
多重背包问题
第$i$个物品至多拿$s_i$件
$$ f\left( i,j \right) =\max \left\{ f\left( i-1,j \right) , f\left( i-1,j-v_i \right) +w_i, f\left( i-1,j-2v_i \right) +2w_i,\cdots ,f\left( i-1,j-s_iv_i \right) +s_iw_i \right\} $$
而
$$
f\left( i,j-v_i \right) =\max \left\{ f\left( i-1,j-v_i \right) , f\left( i-1,j-2v_i \right) +w_i, f\left( i-1,j-3v_i \right) +2w_i,\cdots ,f\left( i-1,j-s_iv_i \right) +\left( s_i-1 \right) w_i ,f\left( i-1,j-(s_i+1)v_i \right) +s_i w_i\right\}
$$
变形后得
$$
f\left( i,j-v_i \right) + w_i =\max \left\{ f\left( i-1,j-v_i \right) + w_i, f\left( i-1,j-2v_i \right) +2 w_i, f\left( i-1,j-3v_i \right) +3w_i,\cdots ,f\left( i-1,j-s_iv_i \right) +s_i w_i ,f\left( i-1,j-(s_i+1)v_i \right) +(s_i+1) w_i\right\}
$$
多了一项$f\left( i-1,j-(s_i+1)v_i \right) +(s_i+1) w_i$,因此无法按照完全背包的方式优化
二进制优化
已知$1,2,4,\cdots,2^k$可以由系数$0$和$1$线性组合出$0$-$2^{k+1}-1$。考虑更一般的情况,若想线性组合出$0$-$S$,$S<2^{k+2}$,则猜测可由$1,2,4,\cdots,2^k, C$组合出,其中$C<2^{k+1}$,显然,在$C$一定存在的情况下,可得到的数的范围为$C$-$S$。由于$C<2^{k+1}$,则$C\le2^{k+1}-1$,故$\left[ 0,2^{k+1}-1 \right] \cup \left[ C,S \right] \supseteq \left[ 0,2^{k+1}-1 \right] \cup \left[ 2^{k+1}-1,S \right] =\left[ 0,S \right] $ ,即可用$1,2,4,\cdots,2^k, C$表示任何$<2^{k+2}$的数
因此对于有s[i]件的某个物品$i$,可以打包成$\lceil \log s\left[ i \right] \rceil $ 个物品,每包有$1,2,4,\cdots,2^k, C$件物品$i$,其中$k=\lceil \log s\left[ i \right] \rceil $ -1
int n; // 物品总数
int m; // 背包容量
int v[N]; // 重量
int w[N]; // 价值
// -----------------未优化(完全背包模板)----------------------
int f[N][M]; // f[i][j]表示在考虑前i个物品后,背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k <= s[i] && k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
// -----------------------二进制优化---------------------------
// 读入物品个数时顺便打包
int k = 1; // 当前包裹大小
while (k <= s)
{
cnt ++ ; // 实际物品种数
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2; // 倍增包裹大小
}
if (s > 0)
{
// 不足的单独放一个,即C
cnt ++ ;
v[cnt] = a * s;
w[cnt] = b * s;
}
n = cnt; // 更新物品种数
// 转换成01背包问题
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
说明
- 用二进制优化后,注意物品种数变成$N\times \log M$,问题转换成01背包问题
- 时间复杂度为$O(nm\log s)$
- 因为求的是滑动窗口的最大值,所以多重背包问题需要使用单调队列优化
分组背包问题
每组物品中至多拿1个
实际上是带有约束的01背包问题,状态计算为$f(i, j)=\max \{f(i-1,j),f(i-1,j-v(i,k)) +w(i,k) \}$
模板
int n; // 物品总数
int m; // 背包容量
int v[N][S]; // 重量
int w[N][S]; // 价值
int s[N]; // 各组物品种数
// 读入数据
for (int i = 1; i <= n; i ++ )
{
cin >> s[i];
for (int j = 1; j <= s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
// 处理数据
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 1; j -- )
for (int k = 1; k <= s[i]; k ++ )
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
线性DP
数字三角形
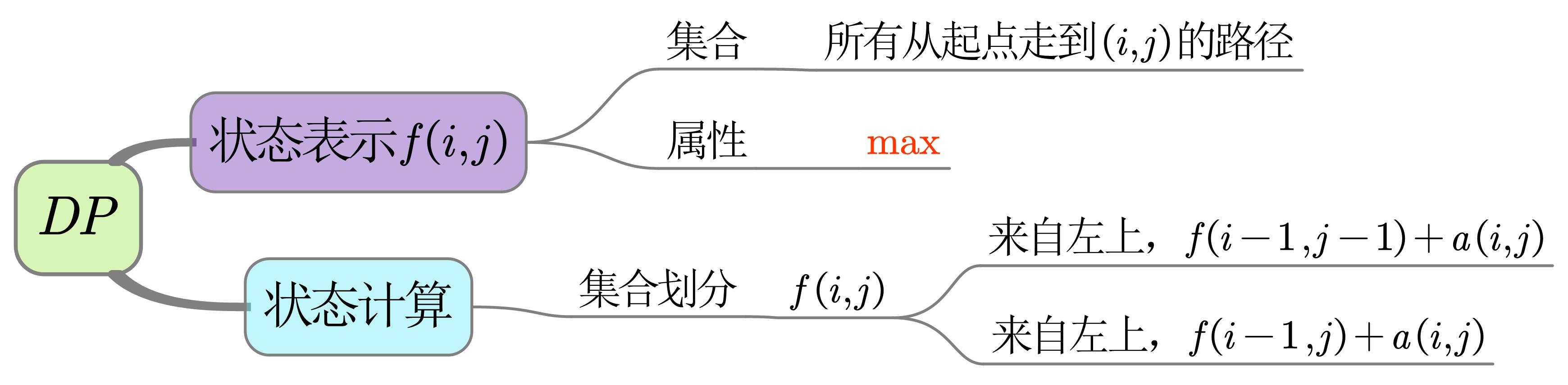
核心代码
// 自顶向下(未压缩`f`)
const int INF = 1e9;
for (int i = 0; i <= n; i ++ )
for (int j = 0; j <= i + 1; j ++ )
f[i][j] = -INF;
f[1][1] = a[1][1];
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for (int j = 1; j <= n; j ++ ) res = max(res, f[n][j]);
说明
- 实际上可压缩
f,此时只能反向遍历行 - 还可自底向上实现,若压缩,只能正向遍历行
- 可以用
0x80初始化f,使得元素都小于-2e9 - 时间复杂度$=O(状态\times 转移)=O(1\times n^2)=O(n^2)$
最长上升子序列
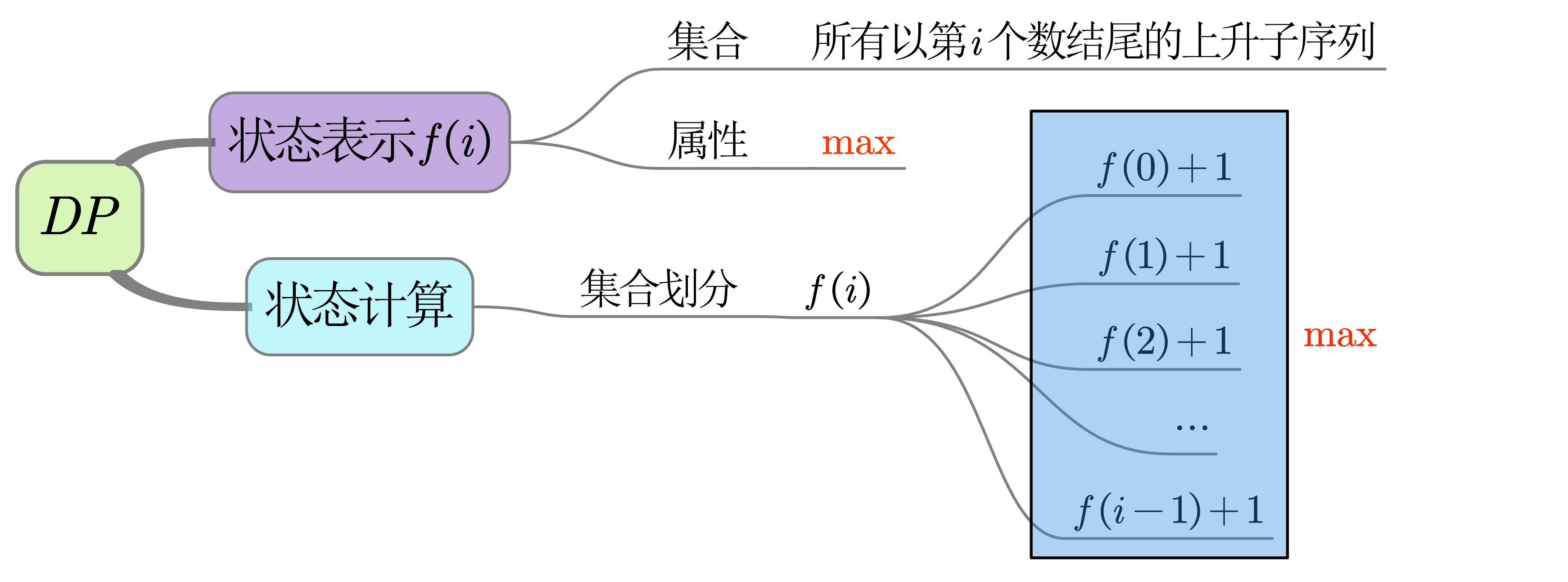
核心代码
// 朴素法
for (int i = 1; i <= n; i ++ ) // 求以a[i]为终点的上升序列中,序列元素个数的最大值,i∈[1,n]
{
f[i] = 1; // 初始化f[i]为1,因为{a[i]}也是一条合法的上升序列
// 状态计算(考虑前i-1个元素)
for (int j = 1; j < i; j ++ )
if (a[j] < a[i]) // 转移条件(升序条件)
f[i] = max(f[i], f[j] + 1); // 状态转移
}
// f[n]表示的是以a[n]为终点的上升序列的最大值,而题目求的是分别以a[1],a[2],...,a[n]为终点的上升序列的最大值
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
// 二分优化
vector<int> stk; //模拟栈
stk.push_back(arr[0]);
for (int i = 1; i < n; ++i) {
if (arr[i] > stk.back())
stk.push_back(arr[i]); // 如果该元素大于栈顶元素,将该元素入栈
else
*lower_bound(stk.begin(), stk.end(), arr[i]) = arr[i]; // 替换掉第一个大于或者等于这个数字的那个数
}
cout << stk.size() << endl;
// yxc二分优化
int len = 0; // 最长上升子序列长度(数组q的长度)
for (int i = 0; i < n; i ++ )
{
// 在数组q中二分查找第1个>= a[i]的数(结果)
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
q[l + 1] = a[i]; // 在长度为l的上升序列中,最小末尾元素是a[i]
len = max(len, l + 1); // q[l] < a[i] < q[l + 1],更新数组q的长度(如果在q末尾插入,则按l + 1更新len
}
printf("%d\n", len);
说明
- 朴素法时间复杂度$=O(状态\times 转移)=O(n\times n)=O(n^2)$
- 改进(贪心+二分)
- 令数组
q保存长度为i的上升子序列末尾元素的最小值,例如125和123优先保存123的3,因为它更能接上的后缀种类更多 q[]是单调递增的,否则存在q[i-1]>q[i],说明长度为i的上升子序列的最小末尾元素比长度为i-1的还小,这与q[i-1]的定义不符- 为了使上升子序列最长,应在
q[]中找到<a[i]的最大q[j],使得q[j]<a[i]<q[j+1],此时子序列的长度为j+1,且q[j+1]=a[i]。这步用整数二分实现 - 改进后,时间复杂度变为$O(n\log n)$
- 令数组
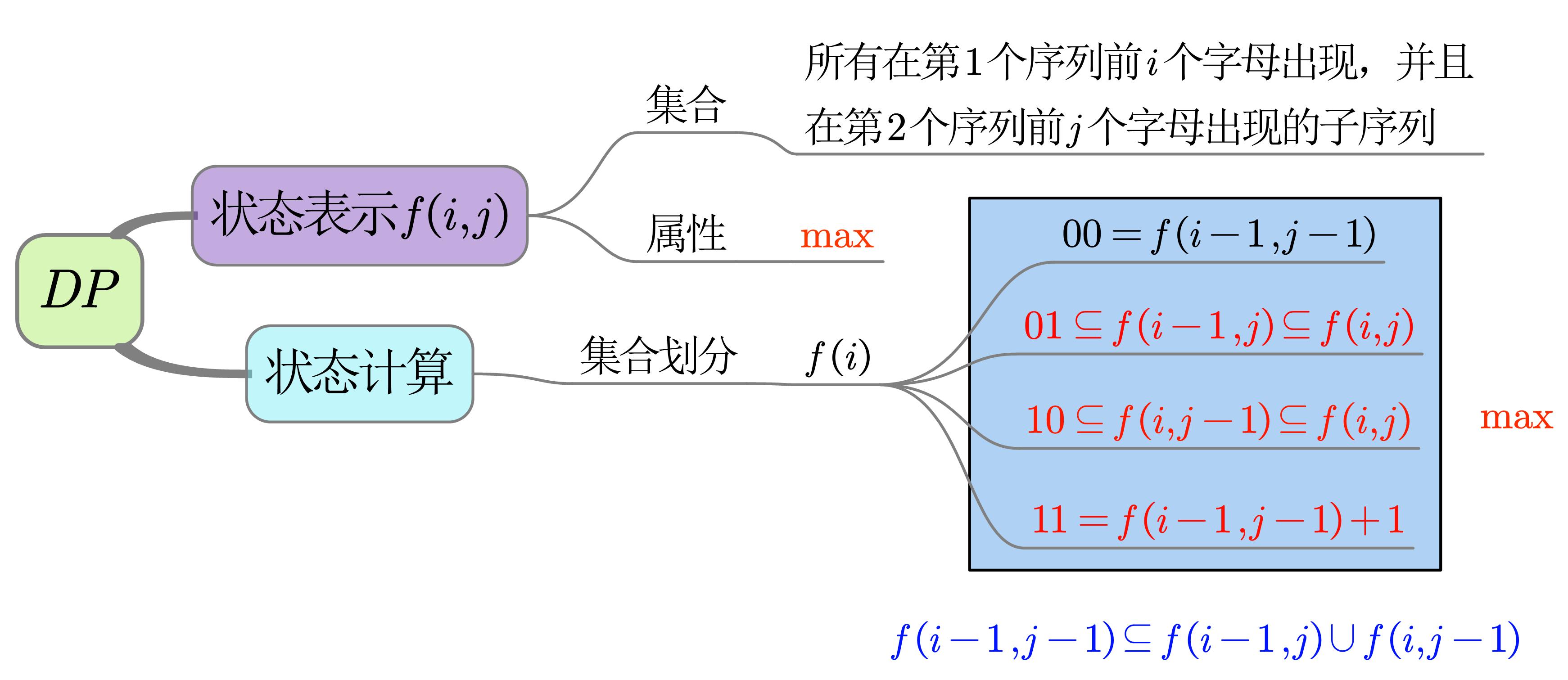
最长公共子序列
核心代码
char a[N], b[N];
int f[N][N];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);//情况01和10,这两种情况已经包含了情况00
if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);//情况11
// if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1; //相等时直接取情况11也能过,但是上一行直接无脑取max,不用考虑证明了
}
printf("%d\n", f[n][m]);
说明
- $00$,$01$,$10$,$11$,表示$f(i,j)$选不选
a[i],b[j]的四种情况,$0$表示不选,$1$表示选(见动态规划(二)1:07:00处) - 难点
- $f(i-1,j)$并不是$01$的等价形式,但$01\subseteq f\left( i-1,j \right) \subseteq f\left( i,j \right) $ ,因此$\max f(i-1,j)$包含了$\max(01)$,且剩余的部分也是属于$f(i,j)$的,故可用$f(i-1,j)$代替$01$。同理$f(i,j-1)$可代替$10$
- 若$C\subseteq A\cap B$,则$\max \left( A,B,C \right) =\max \left( A,B \right) $ 。由于$f\left( i-1,j-1 \right) \subseteq f\left( i-1,j \right) \cup f\left( i,j-1 \right) $ ,故无需考虑$00$的情形,而只需考虑$01$,$10$和$11$的情况
- 时间复杂度$=O(状态\times 转移)=O(n^2\times 1)=O(n^2)$
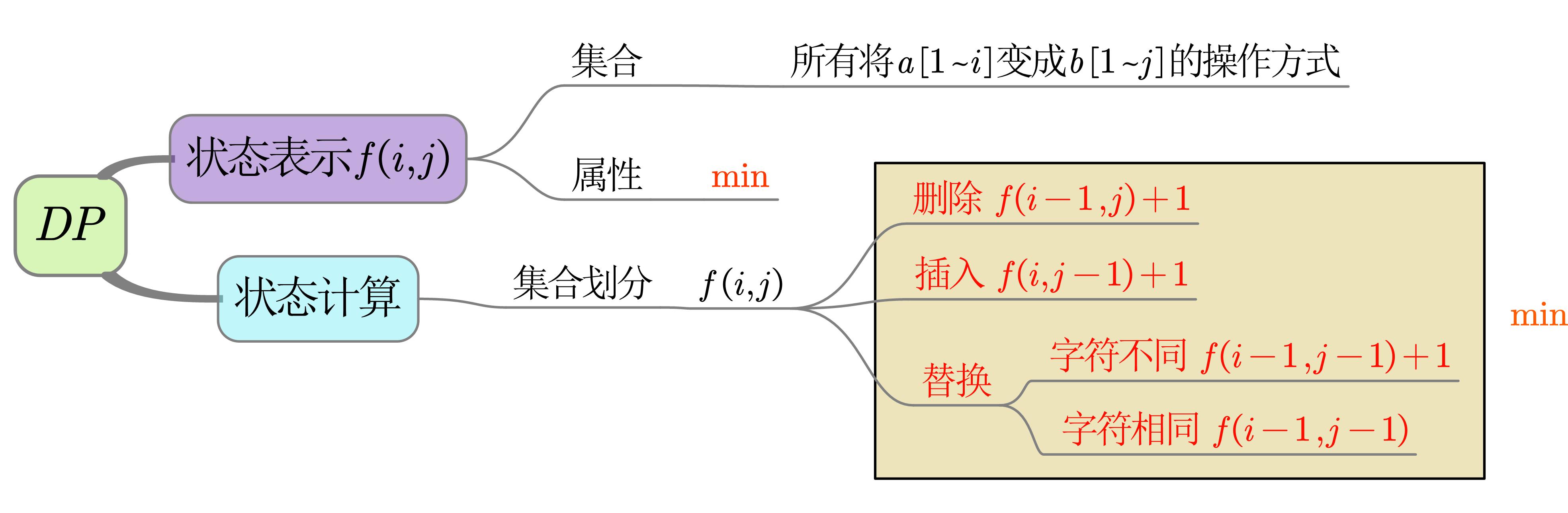
最短编辑距离
给定两个字符串A和B,只允许对A进行字符插入,字符删除和字符替换,求把A变成B的最少操作次数
核心代码
// 初始化边界
for (int i = 0; i <= m; i ++ ) f[0][i] = i; // 把B变成空串需要删除字符的次数
for (int i = 0; i <= n; i ++ ) f[i][0] = i; // 把空串B扩充成A需要插入字符的次数
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
}
printf("%d\n", f[n][m]);
说明
- 时间复杂度$=O(状态\times 转移)=O(n^2\times 3)=O(n^2)$
区间DP
石子合并:相邻两堆石子可以合并,代价为二者石子数的和,求最小代价

核心代码
int s[N]; // 前缀和
int f[N][N];
for (int i = 1; i <= n; i ++ ) s[i] += s[i - 1]; // 初始化前缀和
for (int len = 2; len <= n; len ++ ) // len=1时不合并(类似归并排序的merge)
// 固定窗口大小,从小到大遍历
for (int i = 1; i + len - 1 <= n; i ++ )
{
// 固定窗口左端点,则可确定窗口右端点,注意边界
int l = i, r = i + len - 1;
// 窗口内划分
f[l][r] = 0x7f7f7f7; // 初始化为无穷大
for (int k = l; k < r; k ++ )
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
printf("%d\n", f[1][n]);
说明
- 时间复杂度$O(n^3)$
计数类DP
把n拆分成1~n的和的方案数(不考虑顺序)
有多种考虑方式,对应多种状态转移方程,但时间复杂度一样
完全背包解法
-1601813633686.jpg)
可以看做有$n$种物品,第$i$种物品的体积为$i$,背包的容量为$n$,每个物品可以拿无数次,求装满背包的方案数
假设当前背包容量为$j$,则第$i$个物品至多装$k=\lfloor \frac{j}{i} \rfloor $ 个
已知
$$ f\left( i,j \right) =f\left( i-1,j \right) +f\left( i-1,j-i \right) +f\left( i-1,j-2i \right) +\cdots +f\left( i-1,j-ki \right) $$
当$j <i$时,$j -i < 0$,$f(i,j)=f(i-1,j)$
当$j\ge i$时,$j -i \ge 0$,有
$$ f\left( i,j-i \right) =f\left( i-1,j-i \right) +f\left( i-1,j-2i \right) +f\left( i-1,j-3i \right) +\cdots +f\left( i-1,j-ki \right) $$
对比可得状态转移方程
$$
f(i,j)=f(i-1,j)+f(i,j-i)
$$
综上,当$j <i$时,$f(i,j)=f(i-1,j)$;当$j\ge i$时,$f(i,j)=f(i-1,j)+f(i,j-i)$。特别的$f(0,*)=1$
核心代码
// 未压缩f
f[0][0] = 1;
for (int i = 1; i <= n; i ++)
for (int j = 0; j <= n; j ++)
if (j >= i) f[i][j] = (f[i - 1][j] + f[i][j - i]) % mod;
else f[i][j] = f[i - 1][j];
cout << f[n][n] << endl;
// 压缩f
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = f[j] + f[j - i];
cout << f[n] << endl;
其它算法
-1601816590019.jpg)
当$j$个数中最小值是$1$,则方案数等价于去掉$1$个$1$时的方案数$f(i-1,j-1)$,此时总和为$i-1$,共有$j-1$个数
当$j$个数中最小值$>1$,则方案数等价于$j$个数全都减$1$的方案数$f(i-j,j)$
状态转移方程$f(i,j)=f(i-1,j-1)+f(i-j,j)$
答案$ans=f(n,1)+f(n,2)+……+f(n,n)$
核心代码
f[1][1] = 1;
for (int i = 2; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
数位统计DP
给定两个整数 $a$ 和 $b$,求$ a $ 和$b$之间的所有数字中$0$~$9$的出现次数
思路
第一步:状态表示
第二步:分情况讨论
count(n, x)表示$1$~$n$中,数字$x$出现的次数$0\le x \le 9$
考虑数$x$在n=abcdefg的第$4$位$d$出现的次数,不妨把$n$看成$yyyxzzz$
- 当$000 \le yyy\le (abc-1)$时,$000\le zzz\le 999$
- 当$x\ne 0$时,此时共有$abc\times 1000$次
- 当$x=0$时,由于$abcd$不能全为$0$,因此此时共有$abc\times 1000$次
- 当$yyy=abc$时
- 当$d<x$,$abcdefg<abcxzzz$,此时出现$0$次
- 当$d=x$,$000\le yyy \le efg$,此时出现$efg+1$次
- 当$d>x$,$000\le yyy \le 999$,此时出现$1000$次
特殊处理
- 当求的是最左边那位出现的次数时,$abc$不存在,因此此时只需考虑第2种情况
- 当$x=0$,且遍历到最左边那位时,根据上述讨论,需要把$n$看成$xyyyzzz=0yyyzzz$,这是不合法的,因此当$x=0$时,从左起第2位开始遍历
核心代码
int get(vector<int> num, int l, int r)//从num数组中求出原数字的从l到r位构成的十进制数
{
int res = 0;
for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
return res;
}
int power10(int x)
{
int res = 1;
while (x -- ) res *= 10;
return res;
}
int count(int n, int x)
{
if (!n) return 0; // 特判
// 拆分
vector<int> num;// 用数组将每一位数拆分出来存储
while (n)
{
num.push_back(n % 10);
n /= 10;
}
n = num.size();//让原来的n存储的是原来的数的位数,原来的数现在以数组的形式按十进制位存储在num中
// 核心
int res = 0;
for (int i = n - 1 - !x; i >= 0; i -- ) // 当x=0时,从左起第2位开始遍历
{
// 考虑左起第1位时不存在abc,跳过
if (i < n - 1)
{
res += get(num, n - 1, i + 1) * power10(i);
if (!x) res -= power10(i); // x=0,abc不能全为0,排除这种情况
}
// 尽管左起第1位不存在abc,但存在efg,因此保留这部分
if (num[i] == x) res += get(num, i - 1, 0) + 1;
else if (num[i] > x) res += power10(i);
}
return res;
}
for (int i = 0; i <= 9; i ++ )
cout << count(b, i) - count(a - 1, i) << ' '; // 类似前缀和思想
状态压缩DP
蒙德里安的梦想
在给定大小的网格放入$1\times 2$和$2\times 1$的矩形

状态压缩是通过用二进制数表示状态实现的
当确定横向矩形的位置后,竖向矩形的位置就确定了,因此只需考虑横向矩形的放置方法。
$j$表示当前列的状态,它记录了上一列放入横向矩形的行号,也可理解为当前列被上一列横向矩形捅出的行号,这些行号不可用。例如10010表示上一列第1行和第4行放有横向矩形,即当前列的第1行和第4行不可用。$k$表示上一列的状态,与$j$类似。
假设有$n$行,则状态$j$表示某列$n$个格子的使用情况,格子被占用记为1,空闲记为0。因此这n个格子一共有$2^n$情况,且$0\le j\le 2^n - 1$
集合根据上一列的状态$k$划分,因此共有$2^n$种状态划分方式,当满足横向矩形不碰撞以及剩余部分能放完竖向矩形两个条件时,$f(i,j)$能转移到$f(i-1,k)$
如果dp问题的n比较小(如n<20)就可以尝试考虑状态压缩dp
还不明白就参考这个题解
核心代码
const int N = 12, M = 1 << N; // 最大行数,每列的最大状态数
long long f[N][M];
bool st[M];
// 穷举第i列和第i+1列能放完竖向矩形的情形(找到所有不存在连续奇数个0的情况)
// 预处理,减少重复计算的代价
for (int i = 0; i < 1 << n; i ++ )
{
int cnt = 0;
st[i] = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
if (cnt & 1) {
st[i] = false;
break;
}
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) st[i] = false;
}
f[0][0] = 1; // 全部放竖向矩形,1种方案
for (int i = 1; i <= m; i ++ ) // 遍历1~m列
for (int j = 0; j < 1 << n; j ++ ) // 穷举当前列的可能状态
for (int k = 0; k < 1 << n; k ++ ) // 穷举上一列的可能状态
if ((j & k) == 0 && st[j | k]) // 判断是否满足状态转移条件(不碰撞,能放满)
f[i][j] += f[i - 1][k]; // 状态转移
cout << f[m][0] << endl; // 当放完第0~m-1列后,第m列没有捅出的横向矩形的情形就是最终结果
说明
- 时间复杂度$O(n\times 2^{n} \times 2^{n})=O(n4^n)$,但$n=11$,实际上只需计算$4\times 10^7$次,能在1s内完成
最短Hamilton路径
给定一张 $n$ 个点的带权无向图,点从 $0$~$n-1$ 标号,求起点 $0$ 到终点 $n-1$ 的最短Hamilton路径。 Hamilton路径的定义是从 $0$ 到$n-1$ 不重不漏地经过每个点恰好一次。

将f[i][j]所表示的集合中的所有路线,按倒数第二个点分成若干类,其中第k类是指倒数第二个点是k的所有路线。那么f[i][j]的值就是每一类的最小值,再取个min。而第k类的最小值就是f[i - (1 << j)][k] + w[k][j]。
从定义出发,最后f[(1 << n) - 1][n - 1]就表示所有“经过了所有点,且最后位于点n-1的路线”的长度的最小值,也就是我们要求的答案。
核心代码
memset(f, 0x3f, sizeof f); // 初始化为无穷大
f[1][0] = 0; // 表示只有起点0且最后位于起点0的路线的长度是0,此时点集i的最后一位是1,其余为0,因为点集只有起点0,故i=1
for (int i = 0; i < 1 << n; i ++ ) // 穷举所有可能的点集
for (int j = 0; j < n; j ++ ) // 从当前点集找一个点(二进制串中位为1的位置)
if (i >> j & 1)
for (int k = 0; k < n; k ++ ) // 从当前点集找另外一个点(可以和之前找的相同)
if (i >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); // 尝试从后找的点到达点j
cout << f[(1 << n) - 1][n - 1]; // 所有点都在点集,且终点是n-1
树形DP
给定一个带结点值的树,求一个结点集合,使得集合里任意两个结点都不相邻,且结点值的和最大
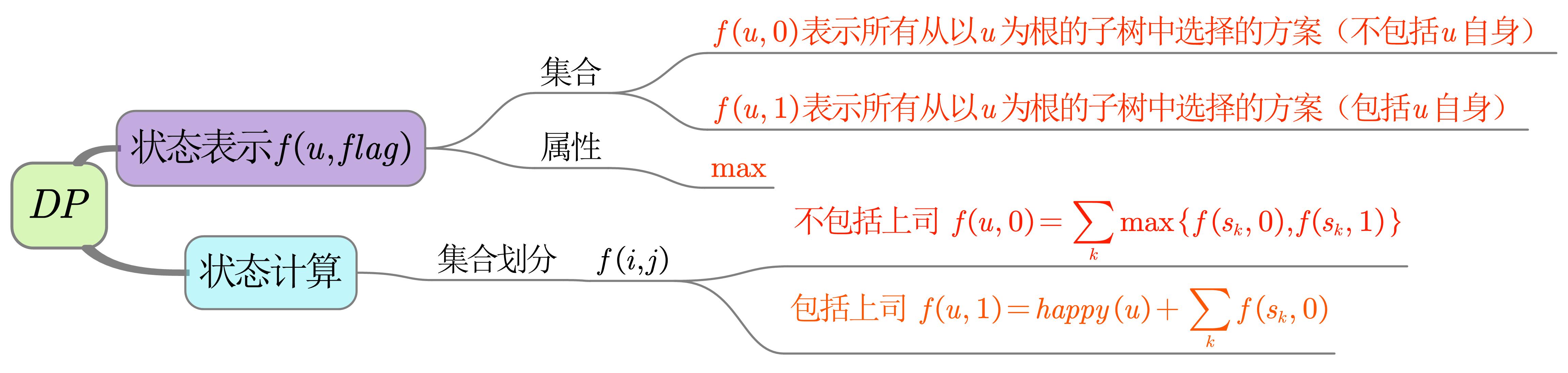
根据有无上司划分集合
- 若上司存在,则不考虑所有直接下属,只考虑所有间接下属
- 若上司存在,则考虑直接下属,在有无下属中选择幸福值最大的那个方案
核心代码
int n;
int h[N], e[N], ne[N], idx;
int happy[N];
int f[N][2];
bool has_fa[N]; // 标记是否存在父节点
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][1] = happy[u]; // 选取根节点的初值为自身的幸福度
// 遍历子树
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i]; // 子结点
dfs(j); // 递归子结点
// 状态转移
f[u][1] += f[j][0];
f[u][0] += max(f[j][0], f[j][1]);
}
}
// 核心
memset(h, -1, sizeof h); // 初始化邻接表头指针
// 读入树结构
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(b, a); // 尽管是无向图,但只需要保留一条边(上司指向下属)
has_fa[a] = true; // 标记存在父节点
}
// 找树根,不存在父节点的就是树根
int root = 1;
while (has_fa[root]) root ++ ;
dfs(root); // 从根节点开始遍历
printf("%d\n", max(f[root][0], f[root][1]));
说明
- 使用邻接表表示树
- DFS+动态规划
记忆化搜索
给一个矩阵,求一条路径,使得它的长度最长,且路径上的值是递减的。(只能往上下左右移动)
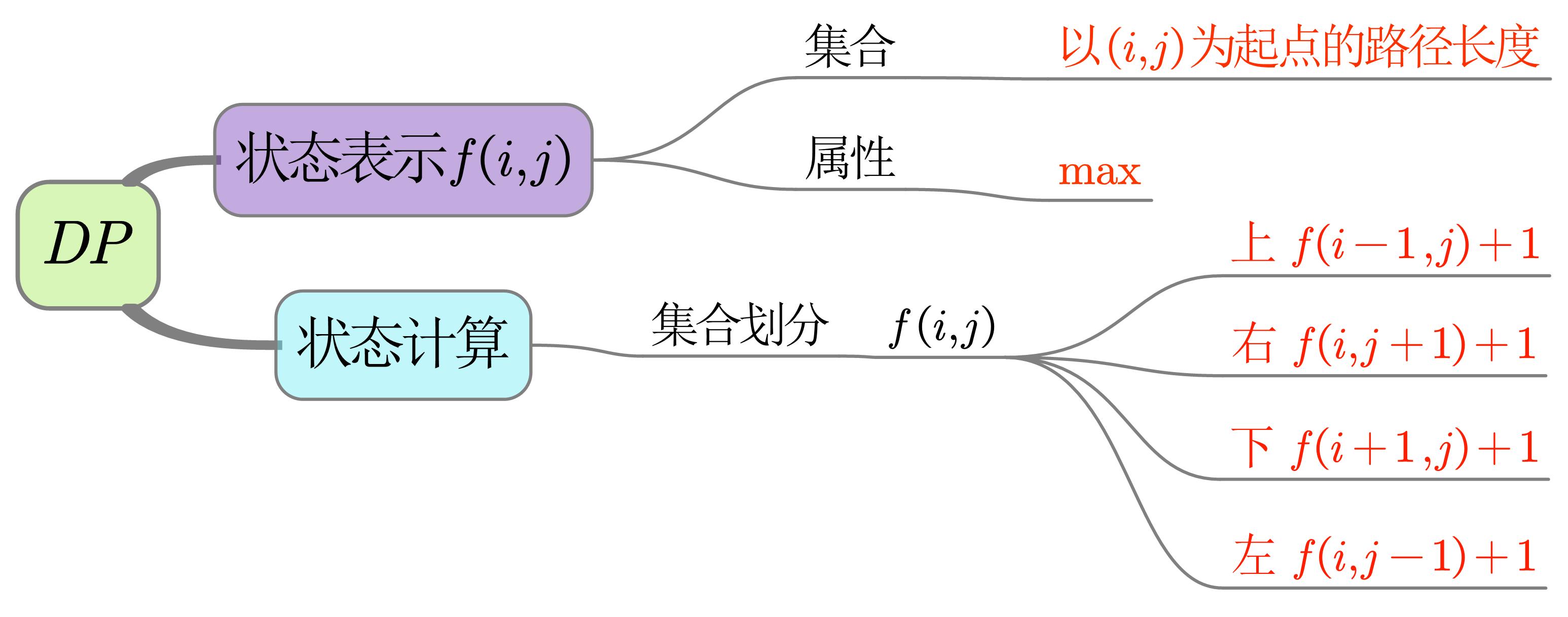
记忆化搜索指保存中间结果,避免重复计算,用空间换时间
优点:代码复杂度相对循环写法较低,得到状态转移方程之后的实现难度相对循环写法较低
核心代码
int g[N][N];
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y)
{
if (f[x][y] != -1) return f[x][y]; // 已经计算过,不必重复计算(记忆化搜索)
f[x][y] = 1;
for (int i = 0; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (g[a][b] < g[x][y])
f[x][y] = max(f[x][y], dfs(a, b) + 1);
}
return f[x][y];
}
memset(g, 0x3f, sizeof g); // 边界为无穷大,不能滑到,可以省去边界判断
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
res = max(res, dp(i, j));
参考资料:y总直播,站内卢盼盼笔记

