线段树入门笔记

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

线段树入门笔记

作者：

T-SHLoRk , 2019-08-28 17:54:30 , 所有人可见 , 阅读 4028

49

53

写在最前，感谢秦淮岸大佬以及其他同学的博客供我参考。

线段树（Segment Tree）

Introduction

线段树这种数据结构可以很好的处理区间查询和区间修改的问题，虽然树状数组也可以通过差分的思想来实现区间修改，但是树状数组通常只能用于区间求和，而线段树能够处理区间最大值/最小值等一系列问题。

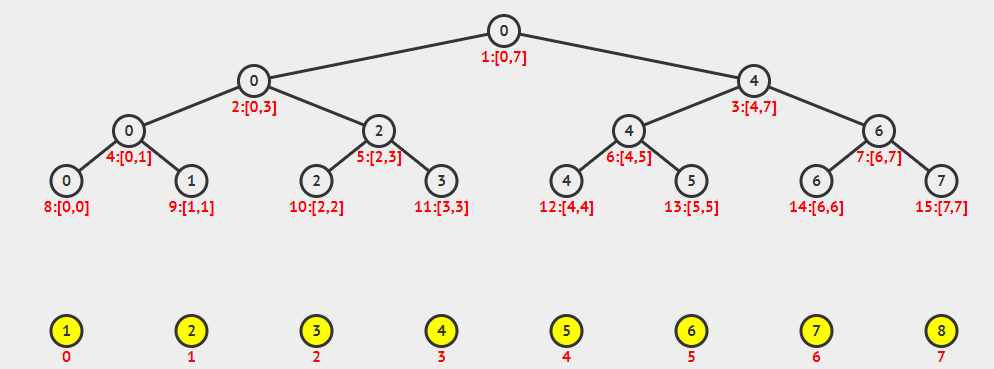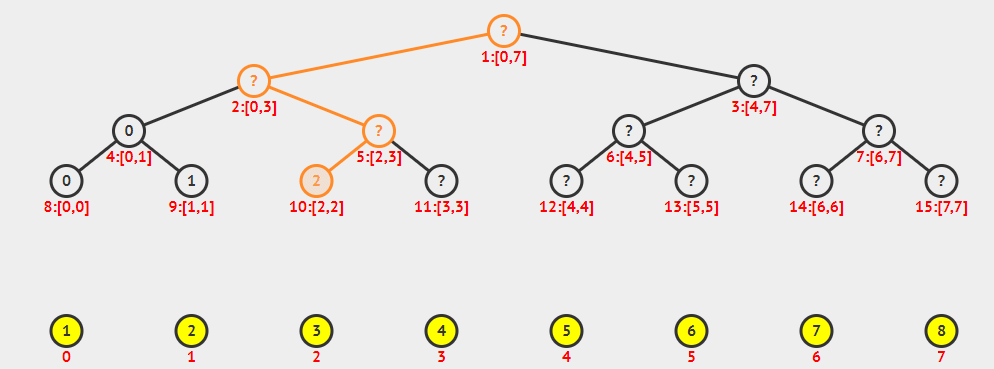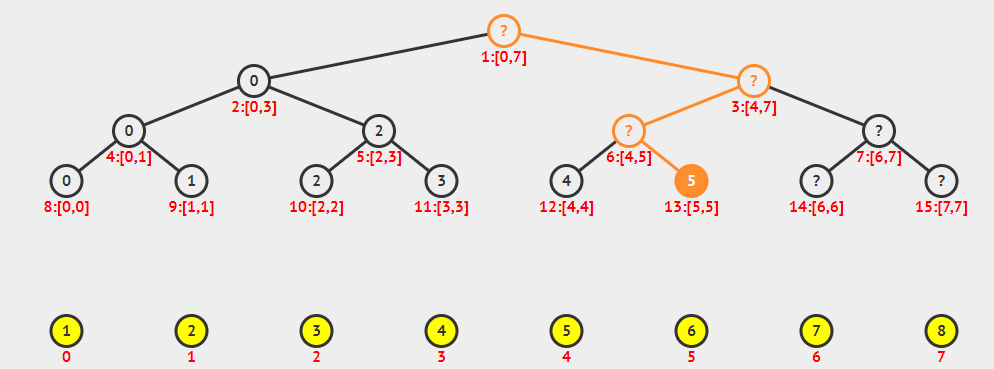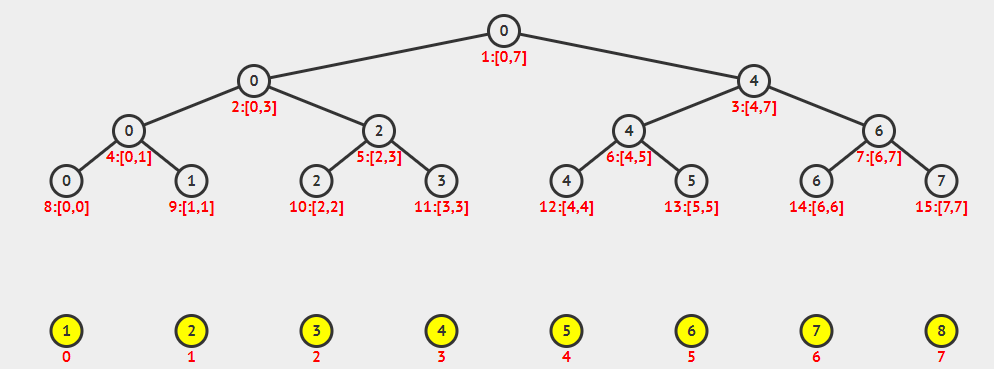
å½å¶_2019_08_04_21_53_05_755.gif

线段树虽然看起来是一个树状结构，但是我们通常使用数组来保存线段树。假设我们原是数组的大小为$n$。

那么线段树的需要开辟的空间一般是$4*n$。

直观上来说，类似于一颗满二叉树好像只需要$2*n$的空间就可以了。

现在我们考虑一个恰好有$N = 2^k + 1$个节点的数组，

那么这棵线段树有$k + 2$层（虽然最后一层只有最左边有两个节点），

但是对于深度为$k + 2$的树，

其满二叉树的节点个数为$2^{k +2} - 1$。

我们可以得到$lim \frac{2^{k+2}-1}{2^k+1}=4$。

所以在极端情况下，我们需要开$4*n$的空间。

在一棵线段树中，每个节点代表的是一个区间，叶子节点代表的是长度为1的区间
。假设一个节点代表的区间是$[L,R]$,

我们有$mid = (L+R)/2$，

那么其左孩子代表的区间就是$[L,mid]$，

右孩子代表的区间是$[mid + 1,R]$。

为了方便起见，线段树数组的长度为$4*n$

其下标我们通常从1开始，那么对应到二叉树，我们可以知道假设一个节点的数组下标为$idx$，

那么其左孩子的数组下标为$idx << 1(idx * 2)$，

其右孩子的数组下标为$idx<<1|1(idx*2+1)$。

建树

在上述动图中，我们可以发现在初始化数组的时候，我们是将节点的左右节点都初始化好了，才初始化根节点，事实上我们也的确如此。这里我们实现一个支持区间求和操作的线段树。

//将处理好的左右儿子节点的值更新给父节点
void push_up(int rt)
{
        tree[rt] = tree[rt << 1] + tree[rt << 1|1];
}

int A[],tree[];
//当前根节点rt对应的原数组区间为[start,end]
void build(int rt,int start,int end)
{
    //  当前节点应该是一个叶子节点了
    if(start == end)
            tree[rt] = A[start];
    else
    {       //  将当前节点代表的区间拆分成两半，分给左子树(rt << 1)和右子树(rt << 1|1)
        int mid = (start + end) >> 1;
        build(rt << 1,start,mid);
        build(rt << 1|1,mid + 1,end);
        push_up(rt);
    }
}
build(1,1,N);

单点修改

//将A[pos]的值修改为val
//当前区间的根节点下标rt，当前区间代表原数组的左右范围l,r，
void update(int rt,int l,int r,int pos,int val)
{
        if(l == r)
      {
            A[pos] = val
            tree[rt] = val;
            return;
      }
        int mid = (l + r) >> 1;
        if(x <= mid)
            update(rt<<1,l,mid,pos,val);
        else
            update(rt<<1 + 1,mid + 1,r,pos,val);
        push_up(rt);
}
update(1,1,N,2,5)//将A[pos] = 5;

区间求和

//当前根节点rt所对应的区间为[l,r],我们希望查询的区间和是[start,end]
int rangeSum(int rt,int l,int r,int start,int end)
{
    //  如果当前节点范围不在目标查找区间内
    //  如果当前节点对应区间恰好完整的在我们的目标区间中，直接返回该节点的值
    //  否则的话，分别在左右子树中查询，并完成累加和
    if(start > r || end < l) 
        return 0;
    else if(start <= l && end >= r)
        return tree[rt];
    else
    {
        int mid = (l + r) >> 1;
        int sum_left = rangeSum(rt << 1,l,mid,start,end);
        int sum_right = rangeSum(rt << 1|1,mid + 1,r,start,end);
        return sum_left + sum_right;
    }
}
rangeSum(1,1,N,2,5)

区间修改

线段树最精华的地方在于线段树的区间修改，如果我们需要修改一段区间$[L,R]$里面的值都加上$delta$，如果我们将其看作若干次单点更新，那么线段树的复杂度就会退化成$O(nlogn)$，这是我们不可接受的。于是线段树创造性的使用了懒惰标记（延迟标记）来实现区间修改，简单的说，就是我们再对一个区间进行修改的时候，我们把这个大区间分成若干个小区间，每次只修改代表这些小区间的节点上的标记，因为一个区间最多分成$O(logn)$个小区间，所以我们可以在$O(logn)$的时间内完成修改。

çº¿æ®µæ .jpg

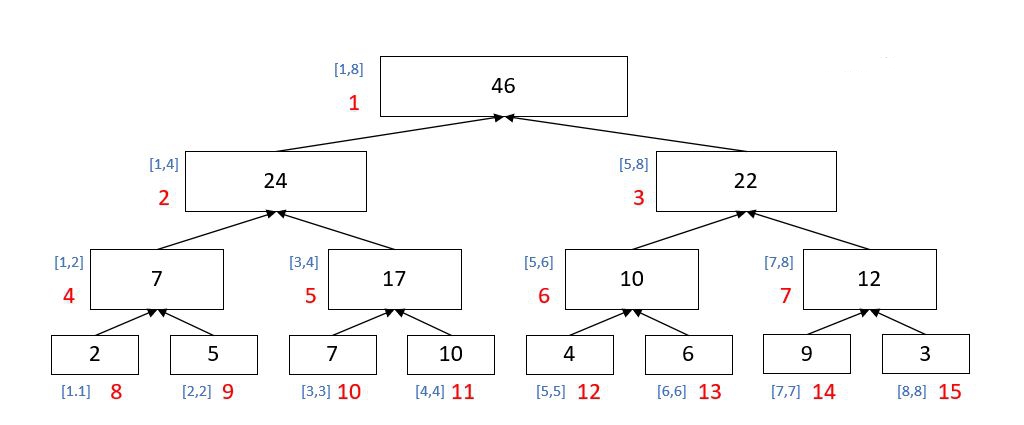
以上图为例，假如我们想将区间$[3,7]$的值都加上$delta$，我们可以发现$[3,7]$可以拆分成$[3,4],[5,6],[7,7]$分别对应上图中的5,6,14号节点，因此我们只需要将这几个节点进行修改。

typedef long long ll;
ll A[N],tree[N],tag[4*N];
//  push_down函数的意义在于将父节点的tag信息传递给两个孩子节点。
//  tree存储的是当前节点区间和，所以将tag传递给孩子节点时，孩子节点的值要加上区间长度乘以tag值
//  tag信息传递给孩子之后，父节点的tag信息就清空啦
void push_down(int rt,int l,int r)
{
        if(tag[rt] != 0)
      {
                int mid = (l + r) >> 1;
                ll lazy = tag[rt];
                int left = rt << 1,right = rt << 1|1;
                tag[left] += lazy,tag[right] += lazy;
                tree[left] += lazy * (mid - l + 1);
                tree[right] += lazy * (r - mid);
                tag[rt] = 0;
      }
}
//  将区间[start,end]的值都加上delta
//  如果当前区间[l,r]是[start,end]的真子集，那么直接修改当前节点对应的区间不用递归向下修改了
//  记住，我们修改的值包括区间和(tree数组)和延迟标记(tag数组)
//  否则我们需要递归查找当前节点rt的左右孩子，在进行递归查找之前我们需要先将当前节点已经存在的延迟标记传下去(push_down函数)。
//  然后再根据左子树是否有目标区间的元素和右子树是否有目标区间的元素进行递归修改。
//  最后不要忘记更新当前节点的值
void updateRange(int rt,int l,int r,int start,int end,ll delta)
{
    if(start <= l && end >= r)
    {
            tree[rt] += (r - l + 1)*delta;
            tag[rt] += delta;
            return;
    }
    push_down(rt,l,r);
    int mid = (l + r) >> 1;
    if(start <= mid) updateRange(rt << 1,l,mid,start,end,delta);
    if(end >= mid + 1)updateRange(rt << 1|1,mid + 1,r,start,end,delta);
    push_up(rt);
}

带区间修改的区间查询

因为我们给每个节点带上了延迟标记，所以之前的区间查询函数我们也需要进行相应的修改。

// 查询区间[start,end]的和
//  如果当前区间节点rt对应的区间[l,r]是[start,end]的真子集，那么直接返回当前节点的值就可以啦。
//  否则我们要将当前节点的延迟标记先传递给左右孩子，然后对左右子树进行查询。
ll rangeQuery(int rt,int l,int r,int start,int end)
{
        if(start <= l && end >= r)
            return tree[rt];
        push_down(rt,l,r);
        int mid = (l + r) >> 1;
        ll res = 0;
        if(start <= mid) res += rangeQuery(rt << 1,l,mid,start,end);
        if(end >= mid + 1) res += rangeQuery(rt << 1|1,mid + 1,r,start,end);
        return res;
}

模板题解：

Acwing243

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const static int N = 100010;
typedef long long ll;
ll A[N],tree[4 * N],tag[4 * N];
void push_up(int rt)
{
    tree[rt] = tree[rt << 1] + tree[rt << 1|1];
}
void push_down(int rt,int l,int r)
{
    if(tag[rt] != 0)
    {
        int mid = (l + r) >> 1;
        ll lazy = tag[rt];
        tree[rt << 1] += (mid - l + 1) * lazy;
        tree[rt << 1|1] += (r - mid) * lazy;
        tag[rt << 1] += lazy;
        tag[rt << 1|1] += lazy;
        tag[rt] = 0;
    }
}
void build(int rt,int l,int r)
{
    if(l == r)
    {
        tree[rt] = A[r];
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1,l,mid);
    build(rt << 1|1,mid + 1,r);
    push_up(rt);
}
void updateRange(int rt,int l,int r,int start,int end,ll delta)
{
    if(start <= l && end >= r)
    {
        tree[rt] += (r - l + 1) * delta;
        tag[rt] += delta;
        return;
    }
    push_down(rt,l,r);
    int mid = (l + r) >> 1;
    if(start <= mid) updateRange(rt << 1,l,mid,start,end,delta);
    if(end >= mid + 1)updateRange(rt <<1|1,mid + 1,r,start,end,delta);
    push_up(rt);
}
ll rangeQuery(int rt,int l,int r,int start,int end)
{
    if(start <= l && end >= r)
        return tree[rt];
    push_down(rt,l,r);
    int mid = (l + r) >> 1;
    ll res = 0;
    if(start <= mid) 
        res += rangeQuery(rt << 1,l,mid,start,end);
    if(end >= mid + 1) 
        res += rangeQuery(rt << 1|1,mid + 1,r,start,end);
    return res;
}
int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i = 1; i <= n ; i ++) 
        scanf("%lld",&A[i]);
    build(1,1,n);
    for(int i = 1; i <= m ; i ++)
    {
        char ch;
        cin >> ch;
        if(ch == 'Q')
        {
            int start,end;
            ll delta;
            scanf("%d %d",&start,&end);
            printf("%lld\n",rangeQuery(1,1,n,start,end));
        }else
        {
            int start,end;
            ll delta;
            scanf("%d %d %lld",&start,&end,&delta);
            updateRange(1,1,n,start,end,delta);
        }
    }
    return 0;
}