2023 蓝桥杯B组省赛 C/C++
A:日期统计
#include<iostream>
using namespace std;
const int N=110;
//数据
int a[N]={5,6,8,6,9,1,6,1,2,4,9,1,9,8,2,3,6,4,7,7,5,9,5,0,3,8,7,5,8,1,5,8,6,1,8,3,0,3,7,9,2,7,0,5,8,8,5,7,0,9,9,1,9,4,4,6,8,6,3,3,8,5,1,6,3,4,6,7,0,7,8,2,7,6,8,9,5,6,5,6,1,4,0,1,0,0,9,4,8,0,9,1,2,8,5,0,2,5,3,3};
int cnt=0;
int m[20]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int main()
{
//for(int i=0;i<100;i++) scanf("%d",&a[i]);
//一个日期一个日期的枚举,能在数据找到就计数
for(int mon=1;mon<=12;mon++)
for(int day=1;day<=m[mon];day++)
{
int Day[10]={2,0,2,3,mon/10,mon%10,day/10,day%10};//当前枚举的日期
int k=0;//数位
for(int i=0;i<100;i++)
{
if(a[i]==Day[k]) k++;
if(k==8)
{
cnt++; break;
}
}
}
cout<<cnt;
return 0;
}
B:01串的熵
#include <iostream>
#include <cmath>
//熵 = -0的个数 * (0的个数/总位数) * log2(0的个数/总位数) - 1的个数 * (1的个数/总位数) * log2(1的个数/总位数)
using namespace std;
int main()
{
double n=23333333;
int o=0; //0的个数
for(o=0;o<=n/2;o++)
{
double Hs=0.0;//熵
Hs-= o * (o/n) * log2(o/n) + (n-o) * ((n-o)/n) * log2((n-o)/n);
if(Hs>11625907.5&&Hs<11625907.6)
{//误差允许范围内
cout<<o<<endl;
break;
}
}
return 0;
}
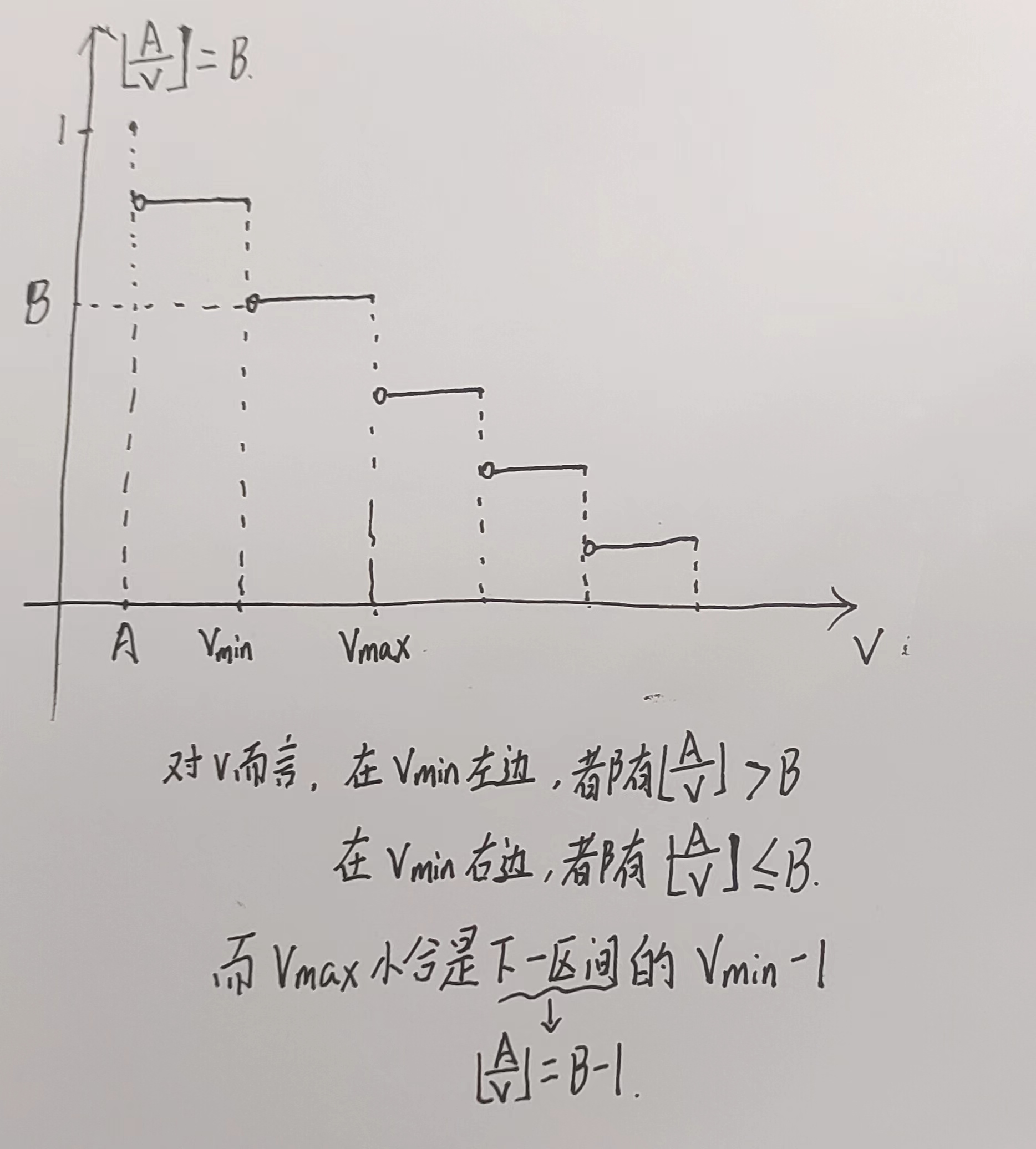
C:冶炼金属
#include<iostream>
using namespace std;
int get(int a,int b)
{//二分a/v==b的区间
int l=1,r=1e9+1;
//r取 1e9+1 是为了防止b=0的情况
while(l<r)
{
int mid=(l+r)/2;
if(a/mid<=b) r=mid;
else l=mid+1;
}
return r;
}
int main()
{
int n; scanf("%d",&n);
int v_min=1,v_max=1e9;
while(n--)
{
int a,b; scanf("%d%d",&a,&b);
v_min=max(v_min,get(a,b)); //求最小值:二分符合a/v==b的区间
v_max=min(v_max,get(a,b-1)-1);//求最大值:二分符合a/v==b-1的区间,结果-1
}
printf("%d %d",v_min,v_max);
return 0;
}
#include<iostream>
#include<cstdio>
using namespace std;
//已知:a>=b*v && a<(b+1)*v
//可得:v>a/(b+1) && v<=a/b
//所以,根据题目的数据,不断缩小范围
int maxx=1e9+10,minx=0;
int main()
{
int n; scanf("%d",&n);
while(n--)
{
int a,b; scanf("%d%d",&a,&b);
maxx=min(maxx,a/b);
minx=max(minx,a/(b+1)+1);
}
printf("%d %d",minx,maxx);
return 0;
}
D:飞机降落
#include<iostream>
using namespace std;
int n;
struct plane
{
int t; //最早降落时间
int d; //可盘旋时间
int l; //降落所需的时间
//t+d:最迟降落时间
}a[15];
bool f[15];
bool dfs(int x,int last)
{
//x:已经降落的飞机数
//last:已经过去的时间
if(x==n) return true; //n架飞机全部搜索完成
for(int i=1;i<=n;i++) //按顺序遍历每架飞机
{
//如果该飞机的最迟降落时间已经过了,那么也就不用遍历了
//最迟降落时间已经过了:t+d<last
if((a[i].t+a[i].d>=last)&&!f[i])
{
f[i]=1;
//飞机会选最早时间降落,最早降落时间或者现在的时间
//即如果现在还没到最早降落时间,就选最早降落时间
//如果现在已经到了最早降落时间,那就现在降落
if(dfs(x+1,max(last,a[i].t)+a[i].l)) return true;
f[i]=0;
}
}
return false;
}
int main()
{
int T; scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d%d",&a[i].t,&a[i].d,&a[i].l);
for(int i=1;i<=n;i++) f[i]=0;
if(dfs(0,0)) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
E:接龙数列
#include<iostream>
using namespace std;
//思路:求最长连续接龙序列长度,再求n-rex即为答案
int dp[15]={0};
//dp[i]:以i为结尾的连续接龙序列长度
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
int rex=0; //最长连续接龙序列长度
for(int i=0;i<n;i++)
{
string s; cin>>s;
int l=s[0]-'0';
int r=s[s.size()-1]-'0';
//两种选择:
//可以选择和以l为结尾的连续序列连接:dp[l]+1
//可以选择不和l相连,依然选择现在的序列:dp[r]
//可得状态转移方程dp[r]=max(dp[l]+1,dp[r]);
dp[r]=max(dp[r],dp[l]+1);
rex=max(dp[r],rex);
}
cout<<n-rex<<endl;
return 0;
}
F:岛屿个数
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
//两个bfs
typedef pair<int,int> PII;
int n,m;
int g[60][60];
bool f[60][60]; //f:判断是否被遍历过
//方向数组
int dx[10]={0,1,0,-1,1,-1,1,-1};
int dy[10]={1,0,-1,0,1,-1,-1,1};
//判断是否为子岛屿
bool bfs1(int a,int b)
{
//子岛屿:另一个岛屿全部位于这个1环内部
//也就是说被1包围就是子岛屿
//那么我们判断它能不能从八个方向冲出1环即可
//一个不被包围的岛,是可以扩展到边界的
memset(f,0,sizeof(f));
queue<PII> q; q.push({a,b});
while(q.size())
{
PII p=q.front(); q.pop();
for(int i=0;i<8;i++)
{
int x1=p.x+dx[i];
int y1=p.y+dy[i];
if(x1<=0||x1>n||y1<=0||y1>m) return true; //成功突出包围
if(g[x1][y1]==0&&!f[x1][y1])
{
q.push({x1,y1});
f[x1][y1]=1;
}
}
}
return false;
}
//将已经计数过的岛屿的f值标为1
void bfs(int a,int b)
{
queue<PII> q; q.push({a,b});
while(q.size())
{
PII p=q.front(); q.pop();
for(int i=0;i<4;i++)
{
int x1=p.x+dx[i];
int y1=p.y+dy[i];
if(x1<=n&&x1>0&&y1<=m&&y1>0)
{
if(g[x1][y1]==1&&!f[x1][y1])
{
q.push({x1,y1});
f[x1][y1]=1;
}
}
}
}
return;
}
int main()
{
ios::sync_with_stdio(false);
int T; cin>>T;
while(T--)
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
char ch; cin>>ch;
g[i][j]=ch-'0';
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(g[i][j]==1)
{
if(!bfs1(i,j)) g[i][j]=0;
}
}
memset(f,0,sizeof(f));
int cnt=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(g[i][j]==1&&!f[i][j])
{
bfs(i,j); cnt++; g[i][j]=0;
}
}
cout<<cnt<<endl;
}
return 0;
}
G:子串简写
#include<bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int k; cin>>k;
string s; cin>>s;
char a,b; cin>>a>>b;
vector<int> v1,v2;
for(int i=0;i<s.size();i++)
{
if(s[i]==a) v1.push_back(i);
if(s[i]==b) v2.push_back(i);
}
long long ans=0;
for(int i=0;i<v1.size();i++)
{
int n=v1[i];
//枚举c1的坐标再二分c2的坐标求有多少个大于等于i + k - 1的数
//int x=lower_bound(v2.begin(),v2.end(),n+k-1)-v2.begin();
int l=0,r=v2.size();
while(l<r)
{
int mid=(l+r)/2;
if(v2[mid]>=n+k-1) r=mid;
else l=mid+1;
}
int x=l;
//x:找到第一个符合要求的下标
//x后面的值都符合 求个数
long long cnt=v2.size()-x;
ans+=cnt;
}
cout<<ans;
return 0;
}
H:整数删除
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
typedef pair<LL,LL> PII;
const int N = 5e5+10;
int n,k,x;
LL cnt[N];// cnt[i]:下标为i的点应该加cnt[i]
priority_queue<PII,vector<PII>,greater<PII>> q; // 小根堆
LL e[N],l[N],r[N],idx;
void init()
{
r[0] = 1;
l[1] = 0;
idx = 2;
}
void add(int k,int x)
{
e[idx] = x;
l[idx] = k;
r[idx] = r[k];
l[r[k]] = idx;
r[k] = idx++;
}
void del(int k)
{
r[l[k]] = r[k];
l[r[k]] = l[k];
}
int main()
{
init();
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
q.push({x,i});
add(l[1],x);
}
// for(int i = r[0] ; i != 1 ; i = r[i] ) cout << e[i] << ' ' ;
while(q.size() > n - k )
{
auto t = q.top(); q.pop();
LL val = t.first, id = t.second;
if(cnt[id])
{
q.push({val+cnt[id],id});
cnt[id] = 0;
}
else
{
if(l[id + 1]) cnt[l[id+1] - 1 ] += val;
if(r[id + 1]) cnt[r[id+1] - 1 ] += val;
del(id+1);
}
}
while(q.size())
{
auto t = q.top(); q.pop();
LL val = t.first, id = t.second;
if(cnt[id]) val+=cnt[id];
e[id+1] = val;
}
for(int i=r[0];i!=1;i=r[i])
{
LL j = e[i];
printf("%lld ",j);
}
return 0;
}
2021 蓝桥杯B组省赛 C/C++
A:空间
#include<iostream>
#include<cmath>
using namespace std;
//1MB = 1* 2^20 字节
//1字节 = 8字
int main()
{
long long x=256*pow(2,20)*8;
cout<<x/32;
return 0;
}
B:卡片
#include<iostream>
using namespace std;
int a[15];
//a[i]:i号卡片的个数
int main()
{
for(int i=0;i<=9;i++) a[i]=2021;
int x;
for(x=1;;x++)
{
bool f=1;
int x1=x;
while(x1)
{
if(a[x1%10]!=0) a[x1%10]--;
else f=0;
x1=x1/10;
}
if(!f) break;
}
cout<<x-1;
return 0;
}
C:直线
#include<iostream>
#include<map>
using namespace std;
typedef pair<double,double> PDD;
//标记{k,b}的直线有没有被讨论过
map<PDD,bool> m;
//所有的点
struct node
{
double x,y;
}p[25*25];
int main()
{
int cnt=0; //点的个数
for(int i=0;i<20;i++)
for(int j=0;j<21;j++)
{
p[cnt].x=i;
p[cnt].y=j;
cnt++;
}//将所有的点都放入p数组
int ans=20+21; //20条竖线 21条横线
for(int i=0;i<cnt;i++)
for(int j=0;j<cnt;j++)
{//遍历每条直线
//横线和竖线不再讨论
if(p[i].x==p[j].x || p[i].y==p[j].y) continue;
//y=kx+b
//k=(y2-y1)/(x2-x1)
double k=(p[i].y-p[j].y)/(p[i].x-p[j].x);
//b=(y1*x2-y2*x1)/(x2-x1)
double b=(p[i].y*p[j].x-p[j].y*p[i].x)/(p[j].x-p[i].x);
if(!m[{k,b}])
{//未被讨论过就计数
m[{k,b}]=true; //标记
ans++; //计数
}
}
cout<<ans;
return 0;
}
D:货物摆放
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1e3+10;
typedef long long int LL;
long long a[N]; //储存因子
int main()
{
LL n=2021041820210418;
int cnt=0; //因子个数
//求因子
for(LL i=1;i*i<=n;i++)
{
if(n%i==0)
{
a[cnt++]=i;
if(i!=n/i)
{//如果i是因子,那么n/i也是
a[cnt++]=n/i;
}
}
}
sort(a,a+cnt);
// cout<<cnt<<endl;
// for(int i=0;i<cnt;i++) cout<<a[i]<<endl;
LL ans=0; //堆放方案数
for(LL i=0;i<cnt;i++)
for(LL j=0;j<cnt;j++)
{
if(a[i]*a[j]>n) continue;
for(LL k=0;k<cnt;k++)
{
if(a[i]*a[j]*a[k]==n) ans++;
else if(a[i]*a[j]*a[k]>n) break;
}
}
cout<<ans;
}
E:路径
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int INF=0x3f3f3f3f;
int g[2030][2030];
int fun(int x,int y)
{//x y的最小公倍数
int a;
for(int i=1;i<=min(x,y);i++)
{
if(x%i==0 && y%i==0) a=i;
}
//a:最小公约数
return (x*y)/a;
}
int main()
{
//按题意建图
for(int i=1;i<=2021;i++)
for(int j=1;j<=2021;j++)
{
if(i==j) g[i][j]=0;
else if(abs(i-j)<=21)
{
g[i][j]=g[j][i]=fun(i,j);
}
else g[i][j]=g[j][i]=INF;
}
//flord
for(int k=1;k<=2021;k++)
for(int i=1;i<=2021;i++)
for(int j=1;j<=2021;j++)
{
g[i][j]=min(g[i][k]+g[k][j],g[i][j]);
}
cout<<g[1][2021]<<endl;
cout<<"10266837";
return 0;
}
F:时间显示
#include<iostream>
using namespace std;
typedef long long LL;
int main()
{
LL x; cin>>x;
x=x/1000;//换算成秒
x=x%(24*60*60);//换算成最后一天的秒数
LL h,m,s;
h=x/3600; m=(x/60)%60; s=x%60;
printf("%02lld:%02lld:%02lld",h,m,s);
return 0;
}
G:砝码称重
深搜枚举暴力
能过5个点
#include<iostream>
using namespace std;
const int N=1e5+10;
int a[111];
bool f[N]={0};
int n;
void dfs(int sum,int i)
{//深搜 枚举所有情况
if(i==n)
{//全部放完 就标记sum
if(sum>=0) f[sum]=true;
return;
}
//选择
dfs(sum+a[i],i+1);//放右边
dfs(sum,i+1); //不放
dfs(sum-a[i],i+1);//放左边
return;
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
dfs(0,0);
int cnt=0;
//计数 有多少个重量能称出来
for(int i=1;i<=N;i++) if(f[i]) cnt++;
printf("%d\n",cnt);
return 0;
}
01背包
正解代码:
#include<iostream>
using namespace std;
const int N=110, M=2e5+10, B=M/2;
//B:偏移量 由于有负数下标
//给每一个j都加一个B 负数在 0 ~ M-1 的范围 正数在 M ~ 2M-1 的范围
int w[N];
bool f[N][M];
//f[i][j]:前i个砝码 能否凑出重量j
int n,m;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>w[i],m+=w[i];
f[0][0+B]=true;
//前0个砝码一定能凑出重量0
for(int i=1;i<=n;i++)
{
for(int j=-m;j<=m;j++)
{
//不选第i个砝码:f[i][j]=f[i-1][j]
//看看前i-1个砝码能否凑出重量j即可
f[i][j+B]|=f[i-1][j+B];
//选第i个砝码 加:f[i][j]=f[i-1][j-w[i]]
//看看前i-1个砝码能否凑出j-w[i]
if(j-w[i]>=-m) f[i][j+B]|=f[i-1][j-w[i]+B];
//选第i个砝码 减:f[i][j]=f[i-1][j+w[i]]
//看看前i-1个砝码能否凑出j+w[i]
if(j+w[i]<=m) f[i][j+B]|=f[i-1][j+w[i]+B];
}
}
int rex=0;
for(int j=1;j<=m;j++) if(f[n][j+B]) rex++;
cout<<rex<<endl;
return 0;
}
H:杨辉三角
#include<iostream>
using namespace std;
typedef long long LL;
int n;
LL C(int a,int b)// 求C a b
{
LL rex=1;
for(int i=a,j=1;j<=b;j++,i--)
{
rex= rex * i / j;
if(rex>n) return rex;
}
return rex;
}
bool cheak(int k)
{
LL l=k*2,r=n;
while(l<r)
{
LL mid=(l+r)/2;
if(C(mid,k)>=n) r=mid;
else l=mid+1;
}
//该行找不到
if(C(r,k)!=n) return false;
//防止找错
if(l!=r) return false;
//找到的数为 第r行 第k列 那么它的前面就有 r * (r+1) / 2 + k 个数
cout<<r * (r+1) / 2 + k+1<<endl;
return true;
}
int main()
{
cin>>n;
//C(34,17)已经大于1e9了,所以从第16斜行开始往上找
for(int k=16;;k--)
if(cheak(k)) break;
return 0;
}