康托展开
介绍
其实一个序列的康托展开值就是求一个序列在所有全排列中从小到大排列是排第几的。也就是说我们把所有序列按照大小都排号了,用这个排号作为它的哈希值,不得不说,巧妙的一匹。
计算思路
假设当前序列为321,询问它的康托展开值cantor(“321”),在所有全排列中比它小的易知有5个,我们首先看最高位的3,想要它这个序列小,一共有两种情况:
- 最高位比3小,后面随意
比3小的有2个,首位比3小,后面的2位无论如何排列,形成的序列一定小于321,所以个数为 $2 * 2!$
- 最高位为3,后面比21小,和思考321的方式相同
最终的结果是上面两种情况加在一起,实际上就是对于序列中的每一位看它的后面有几个比它小的数,用这个数乘上后面剩下的数的全排列数,最后累加到答案上。时刻铭记康托展开值的真正含义,它的计算原理理解起来就很简单。
公式为: $x = a[n] * (n - 1)! + a[n - 1] * (n - 2)! + … + a[1] * 0!$
代码实现(C++)
// 我自己写的代码,不优美但是应该没啥问题
#include <iostream>
#include <algorithm>
using namespace std;
inline int fact(int x)
{
int res = 1;
for (int i = 2; i <= x; ++ i) res *= i;
return res;
}
inline int getHash(string str)
{
int n = str.length();
int hashcode = 0;
for (int i = 0; i < n; ++ i)
{
int cnt = 0;
for (int j = i + 1; j < n; ++ j)
if (str[j] < str[i]) ++ cnt;
hashcode += cnt * fact(n - i - 1);
}
return hashcode + 1;
}
int main()
{
string str = "123";
do
{
cout << str << ' ' << getHash(str) << endl;
} while (next_permutation(str.begin(), str.end()));
}
运行结果

逆康托展开
介绍
康托展开是求一个序列是排第几的,逆康托展开就是问排第n的序列是多少
计算思路
当我们给定一个序列在全排列中从小达到排第n,也就意味着我们知道了$x = a[n] * (n - 1)! + a[n - 1] * (n - 2)! + … + a[1] * 0!$ 左侧x的值,我们除了有x这么一个条件,其实还有一个隐含的条件就是所有的阶乘值都是可以计算的,所以待求的就是 $a[n], a[n - 1], … a[1]$
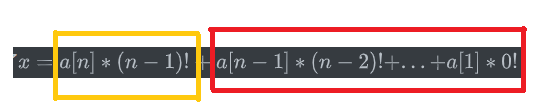
如果我们将红色的部分看为一个数,现在已知x和(n-1)!,通过除法和取余可以分别计算出a[n]和红色的部分,同理我们可以计算得到所有的a。
a[n]的意思是第1位到第n-1位(321,左侧为高位,右侧为低位)中有a[n]个数比第n位的数小,也就是在一个递增的序列中找到第a[n] + 1小的数放到第n位
代码实现(C++)
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
inline int fact(int x)
{
int res = 1;
for (int i = 2; i <= x; ++ i) res *= i;
return res;
}
inline string uncantor(int n, int inx) // 求在长度为n的序列中,从小到达排列,排第inx的序列是多少(从1开始)
{
string res;
int vis[n * n];
memset(vis, 0, sizeof vis);
-- inx; // 比当前序列小的序列有inx个
for (int i = (n - 1); ~i; -- i)
{
int c = inx / fact(i), s = inx % fact(i);
int cnt = 0, num;
for (int j = 1; j <= n; ++ j)
{
if (!vis[j]) ++ cnt;
if (cnt == c + 1) // 找到第c+1小的数
{
num = j;
break;
}
}
vis[num] = 1;
res += num + '0';
inx = s;
}
return res;
}
int main()
{
for (int i = 1; i < 7; ++ i) cout << i << ' ' << uncantor(3, i) << endl;
return 0;
}
运行结果

康托展开应用实例

接触到这个知识点是因为八数码这道题,其实这道题目的核心考点本是bfs,由于做这道题前不久刚刚学习了模拟哈希表,于是想尝试着把题目中使用unordered_map的部分替换为手动哈希。哈希过程中出现的问题是当我们选取的常进制数P较小时,无法满足P进制到10进制的单射关系,而当P的选取使得映射关系满足单射时,映射值又过大,无法作为数组下标,也就无法实现哈希。
对于P的探究
| 数据位数 | 满足单射的最小P值 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 2 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
看样子就是数据位数有几位,在进制转化过程中想要实现单射的P值可选取的最小值就是几,我没太搞懂为什么会有这个关系。回到本题来说的话,如果我们采用常进制数(所有数位采取的P都是相同的),想要9位数满足单射关系,映射后的哈希值最大是478222166,首先是栈上不可能开到这么大的空间,如果开在堆上,大小也在1824MB了,题目的空间要求也无法满足
解决方案
可以发现在一维状态下这些不同的状态就像是一组全排列,而康托展开正是一个一个全排列到一个自然数的双射,用途就是构建哈希表的空间压缩(感觉就是为了这个问题而生的一样)
代码实现
/**
* 写法1-手动哈希,字符串哈希方法在本道题中行不通,需要采用康托展开的方法
* 康托展开只是一种特殊的哈希方法
*/
#include <iostream>
#include <string>
#include <cstring>
using namespace std;
const int N = 4e5 + 1, P = 7; // 总状态数最多也就9!(362880)种,二维下的种类数不太好想,一维下就很简单了,简单的排列问题
string q[N];
int dis[N];
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
inline int fact(int x) // fact(x):计算x!
{
int res = 1;
for (int i = 2; i <= x; ++ i) res *= i;
return res;
}
inline int getHash(string str) // 采用康托展开的方法获取str的哈希值
{
int n = str.length();
int hashcode = 0;
// 计算str序列前比它小序列有多少个
for (int i = 0; i < n; ++ i)
{
int cnt = 0;
for (int j = i + 1; j < n; ++ j)
if (str[j] < str[i]) ++ cnt;
hashcode += cnt * fact(n - i - 1); // 之所以是加法,因为比当前这个序列小的可能是当前这一位小,后面随意,也可能是这位相等,后面小
}
return hashcode + 1; // +1只是为了我想满足康托展开的定义,不加1一样可以ac,这个位置让我进一步理解了哈希的实质
}
int bfs(string start)
{
int hh = 0, tt = -1;
memset(dis, -1, sizeof dis);
dis[getHash(start)] = 0;
q[++ tt] = start;
string end = "12345678x";
while (hh <= tt)
{
// 虽然现在的存储形式是字符串,但是我们需要把字符串转换为矩阵,经过变换后再变为字符串。不过这里的字符串和矩阵之间的转换并不能真的去做而是通过坐标的变换来实现
string t = q[hh ++];
//cout << getHash(t) << endl;
int k = t.find('x');
int x = k / 3, y = k % 3; // 从字符串映射到矩阵
if (t == end) return dis[getHash(t)];
for (int i = 0; i < 4; ++ i)
{
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3)
{
string tmp = t;
swap(tmp[k], tmp[a * 3 + b]); // 从矩阵映射到字符串
if (dis[getHash(tmp)] == -1) // 这个状态之前没有访问过
{
q[++ tt] = tmp;
dis[getHash(tmp)] = dis[getHash(t)] + 1;
}
}
}
}
return -1;
}
int main()
{
string c, start;
for (int i = 0; i < 9; ++ i)
{
cin >> c;
start += c;
}
cout << bfs(start) << endl;
return 0;
}
/**
* 写法2-手动哈希改为unordered_map
* 感觉哈希有问题,所以试了试用库函数,然后就ac了,果然还是有问题
* 之所以采用unorder_map而非map是因为map底层实现是红黑树,具有排序功能,unordered_map底层则是哈希表,本题中想用的就是哈希表,所以采用unordered_map
*/
#include <iostream>
#include <string>
#include <cstring>
#include <unordered_map>
using namespace std;
const int N = 4e5 + 1; // 总状态数最多也就9!(362880)种,二维下的种类数不太好想,一维下就很简单了,简单的排列问题
string q[N];
unordered_map<string, int> dis;
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
int bfs(string start)
{
int hh = 0, tt = -1;
dis[start] = 0;
q[++ tt] = start;
string end = "12345678x";
while (hh <= tt)
{
// 虽然现在的存储形式是字符串,但是我们需要把字符串转换为矩阵,经过变换后再变为字符串。不过这里的字符串和矩阵之间的转换并不能真的去做而是通过坐标的变换来实现
string t = q[hh ++];
int k = t.find('x');
int x = k / 3, y = k % 3; // 从字符串映射到矩阵
if (t == end) return dis[t];
for (int i = 0; i < 4; ++ i)
{
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3)
{
string tmp = t;
swap(tmp[k], tmp[a * 3 + b]); // 从矩阵映射到字符串
if (!dis.count(tmp)) // 这个状态之前没有访问过
{
q[++ tt] = tmp;
dis[tmp] = dis[t] + 1;
}
}
}
}
return -1;
}
int main()
{
string c, start;
for (int i = 0; i < 9; ++ i)
{
cin >> c;
start += c;
}
cout << bfs(start) << endl;
return 0;
}

