BFS(手写队列或者直接用queue)

走迷宫(用queue)： https://www.acwing.com/solution/content/234614/

//一维下标对应的二维下标转化公式: x2 = x1 / n y2 = x1 % m
//二维下标对应一维下标转化公式: x1 = x2 * n + y2
八码数(用queue)： https://www.acwing.com/solution/content/234634/

母亲的牛奶(DFS或者BFS(手写队列))： https://www.acwing.com/solution/content/234853/
全球变暖(DFS或者BFS(手写队列))： https://www.acwing.com/solution/content/234655/

Flood Fill(可以用dfs或bfs实现，但dfs简单，直接用dfs)

动态网格(DFS实现Flood Fill)： https://www.acwing.com/solution/content/234890/
扫雷()： https://www.acwing.com/solution/content/235175/

快速幂(可以用以下的方法，或者是用BigInteger)

BigInteger的使用方法： https://blog.csdn.net/qq_49174867/article/details/123587380
BigInteger a =new BigInteger(“6”);
BigInteger d= a.add(new BigInteger(“4”));
类似的方法：减法:subtract 乘法:multiply 除法:divide 指数:pow(exponent)
求余：reminder() 求模：mod()
区别就在于，mod的模必须为正，否则异常，并且取余的值小于0点话还要加上模数m

快速幂(模板): https://www.acwing.com/solution/content/238319/
转圈游戏(直接使用快速幂模板)： https://www.acwing.com/solution/content/238763/

互质数的个数(快速幂 + 欧拉函数)： https://www.acwing.com/solution/content/238577/

质数

// i <= x/i
试除法判定质数(模板)： https://www.acwing.com/solution/content/239111/
//一定要注意 如果最后x > 1 还有一个质因数
分解质因数(模板)： https://www.acwing.com/solution/content/239121/
筛质数(模板 用埃氏筛)： https://www.acwing.com/solution/content/239125/

约数的个数(分解质因数法 + 870.约数个数)： https://www.acwing.com/solution/content/239411/

质因数个数(分解质因数 + 枚举约数i <= n / i)： https://www.acwing.com/solution/content/239140/

//一个数A如果能组成完全平方数B，那么该完全平方数B一定能由A的质因子偶数次方形成。
//如8可和2组成完全平方数16，而16=(2)^3×2=24，最后质因子的次数一定是偶数次方。
完全平方数： https://www.acwing.com/solution/content/239147/

01背包+筛质数： https://www.acwing.com/blog/content/51694/

约数

试除法求约数(模板): https://www.acwing.com/solution/content/238884/
//int范围内 一个数的约数最多为1600个
//10的9次方范围内 一个数的约数最多为1344个

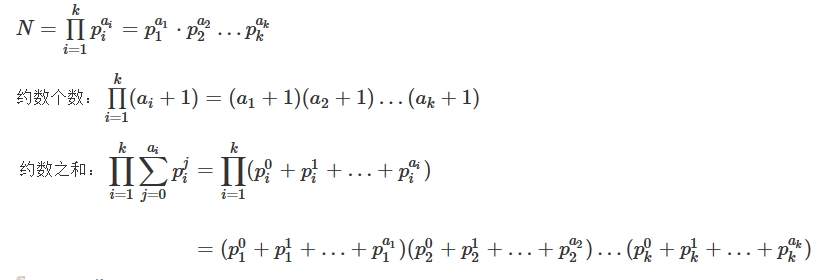
约数个数(模板): https://www.acwing.com/solution/content/238905/
约数之和(模板): https://www.acwing.com/solution/content/238904/
最大公约数(模板): https://www.acwing.com/solution/content/238913/

//求两个数的公约数: 1.求这两个数的最大的公约数 2.求这个最大公约数的所有的约数
公约数(最大公约数+试除法求约数+二分): https://www.acwing.com/solution/content/238931/

//间接考察最大公约数
//每一项与第一项的差一定是d的倍数 每一次去做差和d 找最大公约数 这时候等差数列最短
//当d ！= 0 时， 项数 = (a末 - a初) / d + 1
//当d == 0 时， 项数 = n
等差数列： https://www.acwing.com/solution/content/238940/

并查集

合并集合： https://www.acwing.com/solution/content/235217/
连通块中点的数量： https://www.acwing.com/solution/content/235227/

//有环的连通块，孤立点的数量为0
//树的连通块孤立点的数量>=1
孤立点数量： https://www.acwing.com/solution/content/234344/

哈希

模拟散列表(模板)： https://www.acwing.com/solution/content/235519/

扫雷(dfs + 手写哈希)： https://www.acwing.com/solution/content/234110/