$五边形数的定义$

$f_n = \frac{3n^2-n}{2}$

$1,5,12,22,35,51,70,92,117,145,176,210,247,287,…$

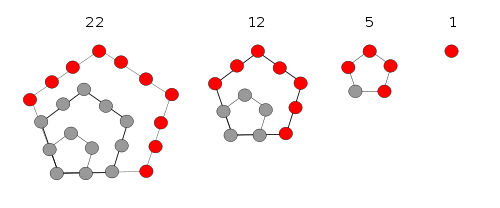
由于上图中红点个数与五边形边长的关系恰好如上式，故得名「五边形数」。

$广义五边形数$

将 $n = 0, 1, -1, 2, -2, 3, -3, 4, -4, …$ 带入 $\frac{3n^2-n}{2}$ 得到

$0,1,2,5,7,12,15,22,26,…$

$欧拉函数$

注意与数论的欧拉函数无关，如下

$$\phi(x) = \prod_{n=1}^{\infty} (1 - x^n)$$

$五边形数定理$

$\phi(n) = \sum_{k = -\infty}^{\infty} (-1)^k x^{\frac{3k^2-k}{2}}$

$= 1 - x - x^2 + x^5 + x^7 - x^{12} - x^{15} + …$

证明

考虑欧拉函数 $x^n$ 项的系数的组合意义，它相当于把 $n$ 拆分成偶数个互不相同的正整数的方案数减去拆分成奇数个互不相同的正整数的方案数。

设现在有一种把 $n$ 拆成 $m$ 个数的方案，将数从大到小排列，例如 $8 = 4 + 3 + 1$。

O O O O
O O O
O

设 $a$ 为最后一行的数，$b$ 为从 $1$ 开始的公差为 $1$ 的极大等差数列长度，如上图，$a=1,b=2$。

若 $b < a（变换1）$，

• $(1) b \ne m \or a \ne m + 1:$ 那么将前 $y$ 行每一行减少一个数，最后添加一行长度为 $y$，易证变换后一定是一个合法的拆分方案，且 $m$ 增加 $1$。
• $(2) b = m, a = m + 1:$ 如下图

O O O O O O
O O O O O
O O O O

变换之后

O O O O O
O O O O
O O O
O O O

出现了有有相同的数的情况，不合法。

设 $k = 1 - a$，那么 $n = (1 - k) + (2 - k) + … + (-2k) = \frac{(-3k+1)*(-k)}{2} = \frac{3k^2-k}{2}$。

也就是说当 $n$ 为广义五边形数时有一种方案无法变换。

若 $b \ge a（变换2）$，

• $(1) a \ne m \or b \ne m:$ 那么将最后一行的 $a$ 个数添加到前 $a$ 行，每行一个，得到一个合法方案且 $m$ 减少 $1$。
• $(2) a = b = m:$ 如下图

O O O O O
O O O O
O O O

进行变换后

O O O O O O
O O O O O
O

行数保持不变，设 $k = a$，$n = k + (k + 1) + (k + 2) + … + (2k - 1) = \frac{3k^2-k}{2}$。

同样，当 $n$ 为广义五边形数时有一种方案无法变换。

接下来我们证明，在一个拆分可以变换的情况下，变换两次一定变为了原来的拆分。

在（变换1）之后，设新的拆分有 $a’,b’$，则 $a’ = b, b’ \ge b$，由此进入(变换2)，进行逆操作，回到原点。

在（变换2）之后，设新的拆分有 $a’,b’$，则 $a’ > a, b’ = a$，由此进入(变换1)，进行逆操作，回到原点。

故可以将奇偶性不同的两个拆分为一组，不算贡献。

故当 $n = \frac{3k^2-k}{2}$ 为广义五边形数时， $x^n$ 的系数为 $(-1)^{k}$。

即

$$\phi(n) = \sum_{k = -\infty}^{\infty} (-1)^k x^{\frac{3k^2-k}{2}}$$

$分拆数$

Luogu P6189 [NOI Online #1 入门组] 跑步

求将正整数 $n$ 拆分为若干个正整数的和（允许同一个数使用多次，这里的拆分是无序的，即 $1+2$ 和 $2+1$ 等价）的方案数。

设 $p(x)$ 为 $x$ 的分拆数，考虑其生成函数

$$\sum_{i=0}^{\infty} p(i) x^i = \prod_{k=1}^{\infty} (1 + x^k + x^{2k} + x^{3k} + …) = \prod_{k=1}^{\infty} \frac{1}{1-x^k} = \frac{1}{\phi(x)}$$

得到

$$\phi(x) \sum_{i=0}^{\infty} p(i)x^i = 1$$

$$(1 - x - x^2 + x^5 + x^7 - x^{12} - x^{15} + …)(1 + p(1)x + p(2)x^2 + p(3)x^3 + …) = 1$$

可以得到式子

$p(k) - p(k - 1) - p(k - 2) + p(k - 5) + p(k - 7) - … = 0$

这样我们就能递推出 $p(k)$ 的值了，由于广义五边形数是 $O(n^2)$ 级别的，所以总复杂度 $O(n\sqrt{n})$。

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int f[N];

int a(int x) {
    return (3 * x * x - x) / 2;
}

int main() {
    int n, p;
    scanf("%d%d", &n, &p);
    f[0] = 1; 
    for (int i = 1; i <= n; i ++ ) {
        for (int j = 1; ; j ++ ) {
            int x = a(j), y = a(-j);
            if (i - x >= 0) {
                if (j & 1) f[i] = (f[i] + f[i - x]) % p;
                else f[i] = (f[i] + p - f[i - x]) % p;
            } if (i - y >= 0) {
                if (j & 1) f[i] = (f[i] + f[i - y]) % p;
                else f[i] = (f[i] + p - f[i - y]) % p;
            }
            if (i - x < 0 && i - y < 0) break;
        }
    }
    printf("%d\n", f[n]);
    return 0;
}