Prim 算法
生成树 Spanning Tree
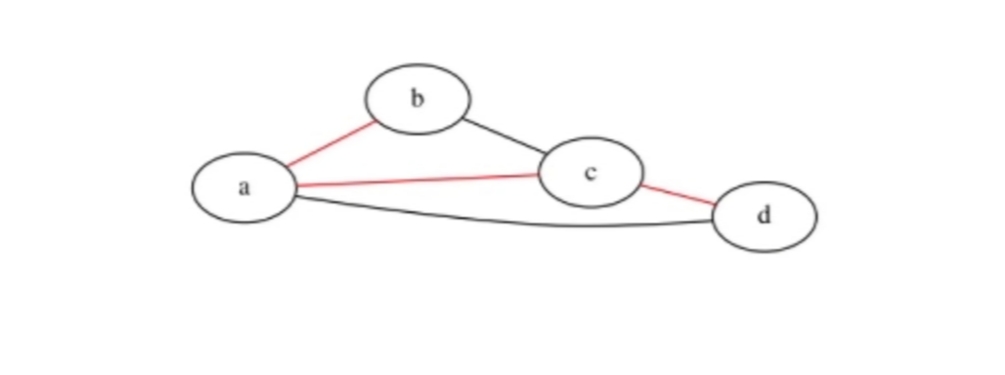
- 对于无向连通图 $G$ 的一个子图,如果它是包含 $G$ 中所有顶点的树,那么这个子图称为 $G$ 的生成树。
- 生成树是无向连通图的包含所有顶点的极小连通子图。
- 在一个无向连通图上,去掉一些边,只保留 $V - 1$ 条边,且保持连通
- 图的生成树不唯一
最小生成树 Minimum Spanning Tree
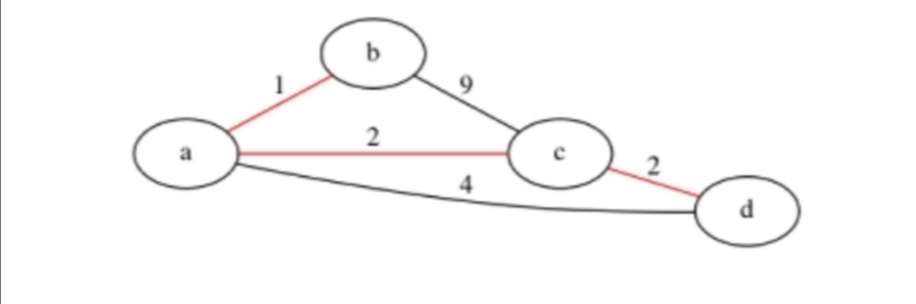
- 生成树各边的权值之和,称为生成树的代价,使代价最小的生成树,称为最小生成树
- 最小生成树在实际生活中有重要的作用:
- 比如,最短修建多少公里的公路可以连通几个城市?
Prim 算法
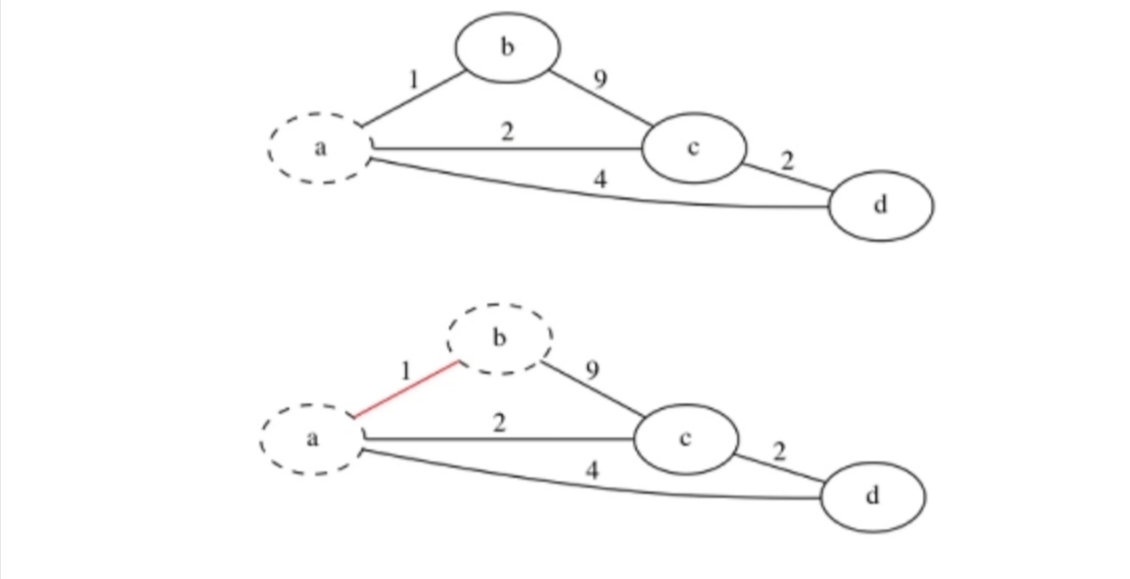
- 假设 $G(V, E)$ 是连通图, $T$ 是 $G$ 上 $\rm MST$ 中边的集合,将点集 $V$ 分为两部分 $\{U\}$ 和 $\{V -U\}$。任选一点 $u_0$,算法从 $U = \{u_0\}$,$T=\{\}$ 开始,重复执行下述操作:
(1) 在所有 $u \in \{U\}$,$v \in \{V - U\}$ 的边(即横跨集合 $\{U\} / \{V - U\}$ 的边)中找最小的边 $(u, v)$ 并入集合 $T$,同时 $v$ 并入 $\{U\}$;
(2) 直到最后 $U = V$ 为止。此时,集合 $T$ 中必有 $V - 1$ 条边,则 $G(U,T)$ 为 $G$ 的最小生成树。
朴素算法时间复杂度 $V^2$,可以用优先队列找最小边的过程,复杂度 $V\log V$。
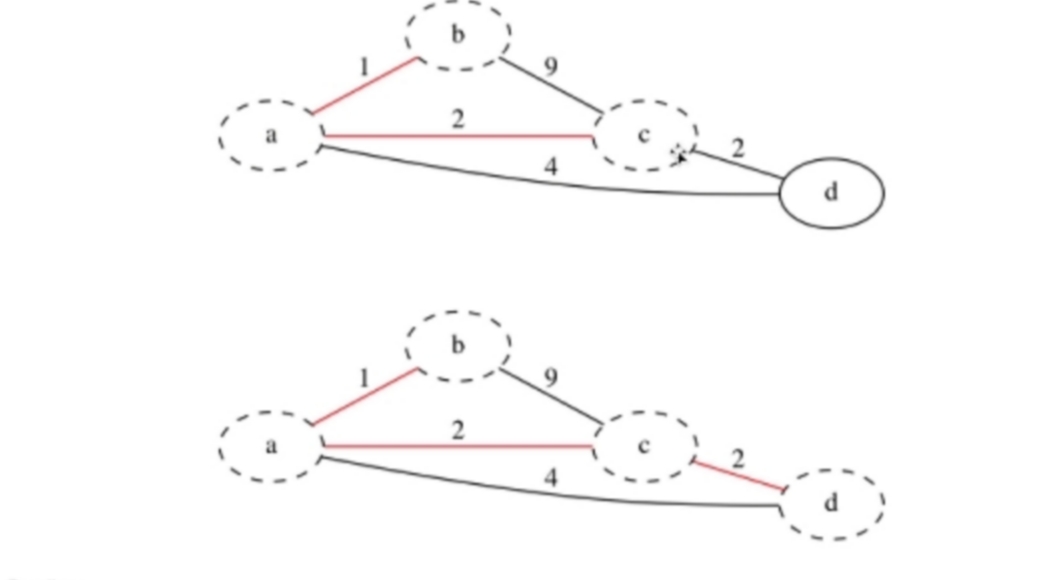
- 可以用 $cost$ 数组来表示 $V-U$ 集合中,每个点与 $U$ 集合中点的最小距离
- $cost$ 数组初始化成无穷大
- $vis$ 数组表示某个点是否在 $U$ 数组中
模板
int prim() {
for (int i = 0; i <= n; ++i) {
cost[i] = INF;
vis[i] = 0;
}
cost[1] = 0;
int res = 0;
for (int i = 0; i < n; ++i) {
// 寻找cost[index]最小的实点index
int index = 0;
for (int j = 1; j <= n; ++j) {
if (vis[j] == 0 and cost[j] < cost[index]) {
index = j;
}
}
vis[index] = 1; // 把实点变成虚点
res += cost[index]; // 累加权值
// 修改与index相连的所有实点
for (int j = 1; j <= n; ++j) {
if (vis[j] == 0 and cost[j] > adj[index][j]) {
cost[j] = adj[index][j];
}
}
}
return res;
}
Kruskal 算法
用贪心的方式选择边
- 思路:能否尽可能挑选比较小的边加入 $\rm MST$ 中?只要不产生回路即可。
- 首先,所有点都属于各自的树,构成一个森林。从小到大选择不构成回路的边加入到 $\rm MST$ 中,直到所有点成为一颗树。
- 可以使用并查集!
- 步骤:
(1) 所有边按照从小到大的顺序排列
(2) 如果边连续的两个点不属于同一集合,则合并,并把这条边加入 $\rm MST$
(3) 重复步骤(2),直到所有点在一个集合中
复杂度 $E\log E + E\alpha(V)$,其中 $E\log E$ 是排序时间,$\alpha(V)$ 是并查集一次查询的时间复杂度
比较
- Prim:复杂度 $O(V^2)$
- Kruskal: 复杂度 $E\log E$
- 稀疏图:$V$ 和 $E$ 同数量级,Prim 是 $O(V^2)$,Kruskal 是 $O(V\log V)$ (一般出题是用稀疏图,因为稠密图没什么可优化的)
- 稠密图:$E$ 和 $V^2$ 是同数量级,Prim 是 $O(V^2)$,Kruskal 是 $O(V^2\log V^2)$
模板
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::sort;
const int N = 5005;
const int M = 200005;
// 用于存边
struct Edge{
int u, v, w;
bool operator< (const Edge& edge) const{
return w < edge.w;
}
};
int n, m;
Edge graph[M];
int father[N];
int mst;
int find(int x) {
if (father[x] == x) return x;
return father[x] = find(father[x]);
}
void merge(int x, int y) {
father[find(x)] = find(y);
}
bool kruskal() {
for (int i = 1; i <= n; ++i) father[i] = i;
int cnt = 0; // cnt记录几次合并
sort(graph, graph + m);
for (int i = 0; i < m; ++i) {
Edge e = graph[i];
int u = e.u, v = e.v, w = e.w;
if (find(u) != find(v)) {
merge(u, v), mst += w, cnt++;
if (cnt == n - 1) return true;
}
}
return false;
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; ++i) {
cin >> graph[i].u >> graph[i].v >> graph[i].w;
}
if (kruskal()) cout << mst << '\n';
else cout << "orz\n";
return 0;
}
最小生成树有两个非常重要的性质,一般的题都离不开这两个性质
-
回路性质:
在原图上任取一个环,环上权值最大的边一定不出现在最小生成树中 -
切割性质:
把节点分为S和T两部分,在所有连接S和T的边中,边权最小的那条一定出现在最小生成树中
用这两个性质可以做很多经典题,比如次小生成树,比如动态加边的最小生成树,比如Codeforces 888G

