动态规划 – 0 1背包问题

动态规划能很好的解决背包问题，并且很多动态规划的题目，都可以转换成背包问题。这是动态规划的第一篇文章，将通过 0 1 背包问题详细讲述如何使用动态规划分析问题，求解问题。即便之前只听说过动态规划这个次，都能很容易理解。

什么是 0 1 背包问题

雪灿同学带着一个背包到了一个有黄金的小岛，小岛上有一些金块。

每个金块的体积和价值不同。因为金块的纯度不同，所以体积大的金块价值不一定大。雪灿使用仪器检测了所有金块，知道了每个金块的体积和价值。

在背包能装下的前提下，雪灿想尽可能的装回价值总量的金子。应该怎么选择金块呢？

这就是 0 1 背包问题。

有 N 种物品，和一个背包。并且给出每种物品的体积 v 和价值 w 以及背包的容量 V。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，并且总价值最大，输出最大价值。

例如我们有 4 件物品和一个容量为 5 的背包。这四件物品的对应的体积和价值分别是：

• 第一件物品：体积 1，价值 2。
• 第二件物品：体积 2，价值 4。
• 第三件物品：体积 3，价值 4。
• 第四件物品：体积 4，价值 5。

我们可以选择把第一件物品和第四件物品放入背包，体积是 1 + 4 = 5，没有超过背包容量，价值是 2 + 5 = 7。

我们可以选择把第二件物品和第三件物品放入背包，体积是 2 + 3 = 5，没有超过背包容量，价值是 4 + 4 = 8。

我们可以选择把第一件物品和第三件物品放入背包，体积是 1 + 3 = 4，没有超过背包容量，价值是 2 + 4 = 6。

还有其它选择方法。

我们的目的是，找到一种选择方案，使得选择物品的总价值最大，然后输出总价值。

动态规划解题步骤

动态规划问题，一般从三个步骤进行考虑。

第一个步骤是状态的表示。

所谓的状态，就是一个未知数。我们用f[i][j]表示从前 i 种物品中进行选择，并且选出的物品总体积小于等 j 时所能得到的最大价值。每个f[i][j] 表示一个状态。

例如f[3][4] 表示用从前 3 件物品中选择，并且选出的物品总体积小于等于 4 时所能得到的最大价值。

例如f[2][5] 表示用从前 2 件物品中选择，并且选出的物品总体积小于等于 5 时所能得到的最大价值。

状态 f[i][j] 有两个约束，一是从前 i 种物品中选择，二是选出物品的总体积小于等于过 j 。f[i][j] 保存的是在这两个条件的约束下，能获得的最大值。

把 0 1 背包问题的所有状态看成一个集合，这个集合中包含的元素为：f[0][0] ~ f[N][V]。每一个元素 f[i][j]的含义是：从前 i 种物品中进行选择，选出的物总体积小于等 j 时所能得到的最大价值。

f[N][V] 的含义是从前 N 件物品中选择，并且选出的物品总体积小于等于 V 时所能得到的最大价值。f[N][V] 就是我们要找的答案。

现在的目的是想办法把所的 f[i][j] 都求出来。

第二个步骤是状态计算。

所谓的状态计算是指，如何将每一个状态计算出来。也就是把每一个 f[i][j] 算出来。

把 从前 i 种物品中进行选择，选出的物品总体积小于等于 j 的所有选择方案获得的价值看做一个集合g[i][j]， f[i][j] 就等于该集合中的最大值。

对于上面的例题，g[2][3] 表示从前 2 种物品中选择，总体积小于等于 3 的所有选择方案获得的价值的集合。

选择方案有 三 种：方案1. 只选物品1，价值为 2。 方案2. 只选物品 2，价值为 4。方案3. 同时选物品 1 和物品 2，价值为 6。

g[i][j] = {2， 4， 6}。f[i][j] 为该集合中的最大值 6。

我们可以将 g[i][j] 这个集合可以划分成互斥的 A B 两部分。

A 部分是选法中不包含第 i 件物品。B 部分是选法中包含第 i 件物品。

A 部分，等价于从前 i - 1 件物品中选择，选出的物品总体积小于等于 j 的所有方案获得的价值集合，也就是 g[i - 1][j]。g[i - 1][j]这个集合中的最大值是 f[i - 1][j]，所以 A 部分的最大值就是 f[i - 1][j]。

B 部分等价于从前 i 件物品中选择，并且必须选择第 i 件物品，且选出的物品总体积小于等于 j 的所有方案获得的价值集合。

B 部分怎么求呢？直接求不太好求，可以试试曲线救国：

因为 B 部分对应的方案中一定要选择第 i 件物品。这时候有两种情况。

1. 给定的容量能放下第 i 件物品，那么第 i 件物品会占据 $ v_{i} $ 的背包空间，剩下的背包空间为 V - $ v_{i} $ 。可以继续从前 i - 1 种物品中，选出的物总体积小于等 V - $ v_{i} $的物品放入背包中。 从前 i - 1 种物品中进行选择，选出的物总体积小于等 V - $ v_{i} $ 的方案获得的价值集合为 g[i - 1][V - $ v_{i} $] 。所以 B 部分的元素为 g[i-1][V - $ v_{i} $] 中各个元素的值加上 $ w_{i} $ 。g[i-1][V - $ v_{i} $] 中的最大值为 f[i-1][V - $ v_{i} $]， 因此 B 部分的最大值为 f[i-1][V - $ v_{i} $] + $ w_{i} $ 。

2. 给定的容量不能能放下第 i 件物品，这时候背包里就不能放入第 i 件物品，因此 B 部分就是空集。B 部分的最大值为 0。

通过上面分析，我们可以知道，g[i][j] 可以分成两部分，A 部分是不包含第 i 种物品的选法，最大值是 f[i - 1][j]。B 部分是包含第 i 种物品的选法，最大值是 f[i-1][V - $ v_{i} $] + $ w_{i} $ 或 0。所以 g[i][j] 的最大值就是在 A 部分的最大值与 B 部分的最大值取个max，也就是:

例如 g[2][3] 可以划分成两部分，A 部分是不包含第 2 种物品，对应方案1。B部分是包含第 2 种物品，对应方案 2 和方案 3。

A 部分的最大值是 f[2 - 1][3] = f[1][3] = 2。

B 部分的最大值是 f[2 - 1][3 - 2] + $ w_{i} $ = f[1][1] + 4 = 6。

所以集合g[2][3] 的最大值 f[2][3] = max(A，B) = max(2, 6) = 6。

第三个步骤是确定初始值

有些状态是能够直接确定的。

例如 f[0][0]。f[0][0] 的含义是从前 0 件物品中选择，并且选出的物品总体积小于等于0 时所能得到的最大价值。总体积小于等于 0，说明一种物品都不能选择，因此 f[0][0] = 0。同理 f[1][0] = 0，f[2][0] = 0 ··· f[N][0] = 0。

有了这些初始值，通过 i 从 1 遍历 N，j 从 1 遍历 V，就能一步步求出所有的 f[i][j] 了。

例如求 f[1][1]。f[1][1] = max(A, B) = max{f[0][1]，f[0][0] + 2} = max(0，2) = 2。

求 f[1][2]。f[1][2] = max(A, B) = max{f[0][2]，f[0][0] + 4} = max(0，4) = 4。

最后 f[N][V] 就是要找的答案。

这时候就可以写代码了：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];//v 保存体积，w 保存价值
int f[N][N];//保存所有状态

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];

    for(int i = 0; i <= m; i++)//初始化，前 0 中物品中选择
    {
        f[0][i] = 0;
    }

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++)
        {
            if(v[i] <= j)//能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            else//不能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = f[i - 1][j];
        }

    }
    cout << f[n][m] << endl;//f[n][m] 就是答案

    return 0;
}

优化

动态规划的优化一般都是对代码或者状态方程进行一个等价变形。在考虑动态规划问题的时候，一定要先把基本的形式写出来，然后再对它进行优化。

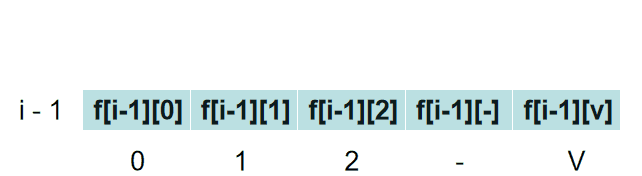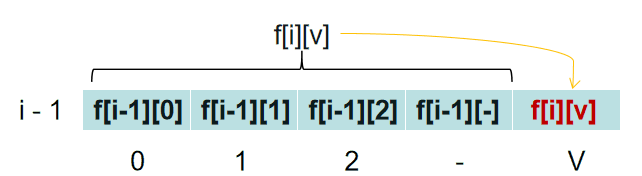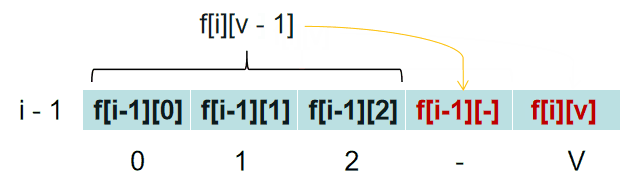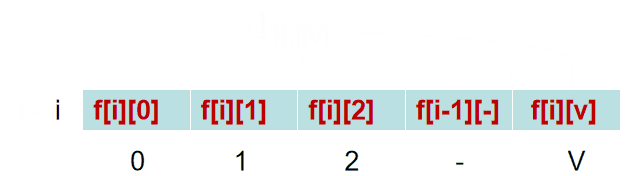
首先，根据优化前的起码，f[i][j] 是从上到下，一行一行这样填满的：

看一下 f[i][j] 的计算公式：f[i][j] = max(A, B)。

只用到了f[i - 1][j]，f[i-1][j - $ v_{i} $] ，即只用到了 f[i - 1] 这一层，并且用到的体积为 j 和 j - $ v_{i} $ ，都是小于等于 j 的。

因此可以从体积为 V 开始，利用f[i - 1]的数据，求解除 f[i][j]，把 f[i][j] 放到 f[i -1][j] 的位置上。

并且，当 背包容量小于 $ v_{i} $ 的时候，f[i][j] = max{f[i - 1][j]，0} = f[i - 1][j]。所以 j 只需要从 V 遍历到 $ v_{i} $ 即可。

写下代码：

//参考yxc
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= v[i]; j -- )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

0 1背包问题到此解决。