参考题解： https://www.acwing.com/solution/content/230686/

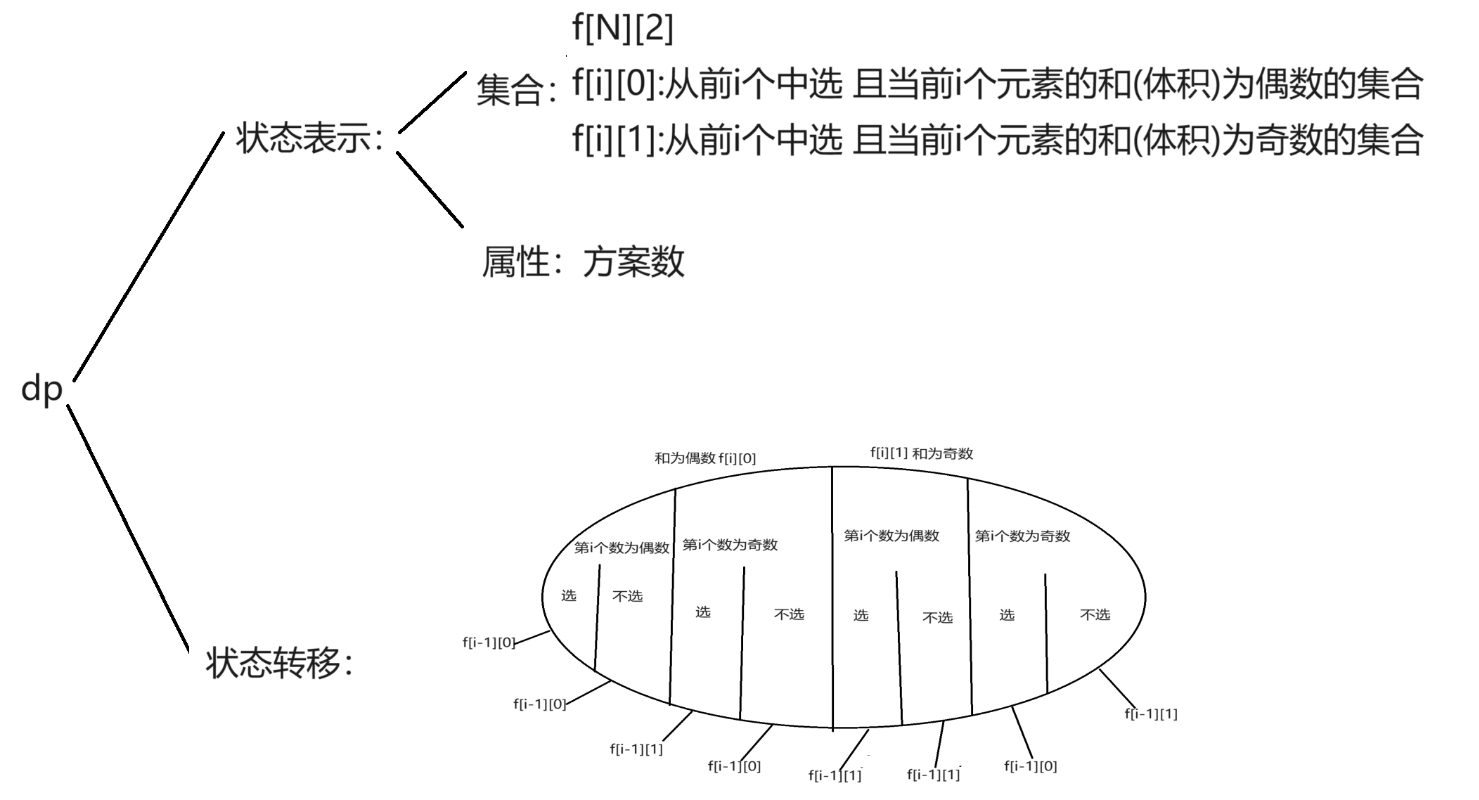
DP

import java.util.*;
public class Main{

    static int N = 1010,mod = 1000000007;
    static int []a = new int[N];
    static int [][]f = new int[N][2];

    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        int T = in.nextInt();
        while(T -- > 0){
            int n = in.nextInt();
            long sum = 0;
            for(int i = 1;i <= n;i ++){
                a[i] = in.nextInt();
                sum += a[i];
                Arrays.fill(f[i],0);
            }
            if((sum & 1) == 1){// 和为奇数 说明 分不了
                System.out.println(0);
                continue;
            }
            f[0][0] = 1;
            for(int i = 1;i <= n;i ++){
                if((a[i] & 1) == 0){
                    f[i][0] = (f[i-1][0] * 2)%mod;
                    f[i][1] = (f[i-1][1] * 2)%mod;
                }
                else{
                    f[i][0] = (f[i-1][0] + f[i-1][1])%mod;
                    f[i][1] = (f[i-1][0] + f[i-1][1])%mod;
                }
            }
            System.out.println(f[n][0]);
        }
    }
}

组合计数

C(0,n) + C(1,n) + C(2,n) + C(3,n) + C(4,n) +…+ C(n,n) = 2^R
C(0,n) + C(2,n) + C(4,n) + C(6,n) + C(8,n) +…+ C(n,n) = 2^(n-1)
C(1,n) + C(3,n) + C(5,n) + C(7,n) + C(9,n) +…+ C(n,n) = 2^(n-1)
C(0,n) - C(1,n) + C(2,n) - C(3,n) + …(-1)^n * C(n,n) = 0

/*
R : 偶数的个数
L ：奇数的个数

如果奇数为奇数个，必定方案数为0

先选 0 -> R 任意个偶数 C(0,R) + C(1,R) + C(2,R) + C(3,R) + C(4,R) + C(R,R) = 2^R
再选 0 2 4...偶数个奇数C(0,L) + C(2,L) + C(4,L) + ... + C(L,L) = 2^(L-1)

乘法原理：最后的方案数为 2^R * 2^(L - 1)
*/


import java.util.*;

public class Main{

    static int mod = 1000000007;

    static long qmi(long a,long k){
        long ans = 1;
        while(k != 0){
            if(k % 2 == 1) ans = (ans * a) % mod;
            a = (a * a) % mod; 
            k /= 2;
        }
        return ans;
    }

    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        int T = in.nextInt();
        while(T -- > 0){
            int n = in.nextInt();
            long r = 0,l = 0;
            for(int i = 0;i < n;i ++){
                int t = in.nextInt();
                if(t % 2 == 0) r ++;
                else l ++;
            }
            //当奇数的个数为奇数时 一方为偶集合 那么另一方必为奇集合
            if(l%2 == 1) System.out.println(0);
            else System.out.println(qmi(2,r)%mod*qmi(2,l-1)%mod);
        }
    }
}