入门：递归（递与归）（与dfs的区别） - 记忆化搜索（递归 + 记忆目的减少重复子问题）-dp（相比递归只有归）

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

入门：递归（递与归）（与dfs的区别） - 记忆化搜索（递归 + 记忆目的减少重复子问题）-dp（相比递归只有归）

作者：

7cghc , 2024-04-11 21:38:27 , 所有人可见 , 阅读 8

结论（用于看完后面逐步讲解快速回忆）
1、优先考虑 dfs（搜索方案数，维护全局最优解 – 以较为深刻理解）
·一般dfs（搜索方案数）都是从最初状态开始（最小值 / 最小子问题, 也就是正序求解，类似于人寻找方案时选择的情况
2、
（1）根据1进行进一步思考：考虑增加返回值dfs(i, ....)返回从i开始考虑i~n的最优解/累加解（最优问题（背包，数字三角形，洗劫）/累加问题（台阶、货币问题）），那么递归的边界就是最终状态（问题所求）的下一个，一般根据返回值的理解来考虑边界条件
·这种问题的边界都是把每个都考虑进去，即对每个进行选择
最优问题

if(i > n) return 0;

累加问题

if(i > n)
{
    if() return 1;//该方案成立，有题目而定
    else if() return 0;//该方案不成立
}

（2）通常的递归思路-大问题分解成子问题，那么递的过程与1和2（1）的过程相反，归的顺序也相反，即刚好是逆过程。那么，递归边界就是最小子问题（如斐波那契数列f[1] 和f[2]，走台阶的f[1] = 1, f[2] = 2），一般较容易得之。 ----------------- 这里不太建议使用此分解子问题方式，不太容易理解，而且再进一步优化成 dp 时，边界问题可能较为复杂，此时的dp遍历顺序为正序（如数字三角形，正序dp的边界比较复杂，不如逆序，逆序dp 对应 1和2（1）的思考方式，边界较为好处理，一般都是 0）
3、再递归2（1）的基础上，增加记忆化数组，数组的维数 = 递归的参数个数都表示状态，即返回值的含义
· 要想实现记忆化搜索那么递归的参数就需要尽可能少
记忆化搜索的本质就是如果递归的参数相同（状态相同），那么对其进行保存，防止重复调用。言外之意递归的参数个数 = 记忆化数组的维数！！！
同时，没必要把影响到递归边界的参数放进来
如在本题中加入一个记录 当前洗劫的价值
4、再递归2（1）*的基础上优化成dp，删去递的过程，因为只有归的过程才是生成答案的过程。注意dp遍历的顺序，与递（归）方式相反，即归的顺序。

-821. 跳台阶
dfs(搜索方案数)

#include<iostream>
using namespace std;

int n, sum;

void dfs(int u)
{
    if(u == n)
    {
        sum++;
        return;
    }
    if(u + 1 <= n) dfs(u + 1);
    if(u + 2 <= n) dfs(u + 2);  
}

int main()
{
    scanf("%d", &n);
    dfs(0);
    cout << sum;
    return 0;
}

递归思路(带返回值) O(2^n)

#include<iostream>
using namespace std;

int n;

int dfs(int u)
{
    if(u == 1) return 1;
    else if(u == 2) return 2;
    else return dfs(u - 1) + dfs(u - 2);

}

int main()
{
    scanf("%d", &n);
    cout << dfs(n);
    return 0;
}

递归和深搜的区别
递归：

递归是一种编程技巧，它在函数内部直接或间接地调用自己，从而解决问题。
递归通常用于解决可以分解为相似子问题的问题，每次递归调用都会缩小问题的规模，直到达到基本情况。
递归可以是深度优先搜索的一种实现方式，但并不局限于此，它可以用于解决各种问题，包括动态规划、分治、回溯等。
深度优先搜索（DFS）：

深度优先搜索是一种遍历或搜索图、树或状态空间的算法。
在深度优先搜索中，从起始节点开始，沿着一条路径尽可能深地搜索，直到到达末端节点或者无法继续搜索为止，然后回溯到上一个节点，继续搜索其他路径。
深度优先搜索通常用于图的遍历、寻找路径、解决拓扑排序等问题，它可以递归或非递归地实现。
虽然递归和深度优先搜索有时候可能会用相似的代码结构，但它们的关注点不同：递归是一种解决问题的编程技巧，而深度优先搜索是一种解决搜索和遍历问题的算法。

记忆化搜索（对递归解决子问题的过程进行优化 - 避免重复计算（使用表示状态的数组进行保存已经算出的结果））
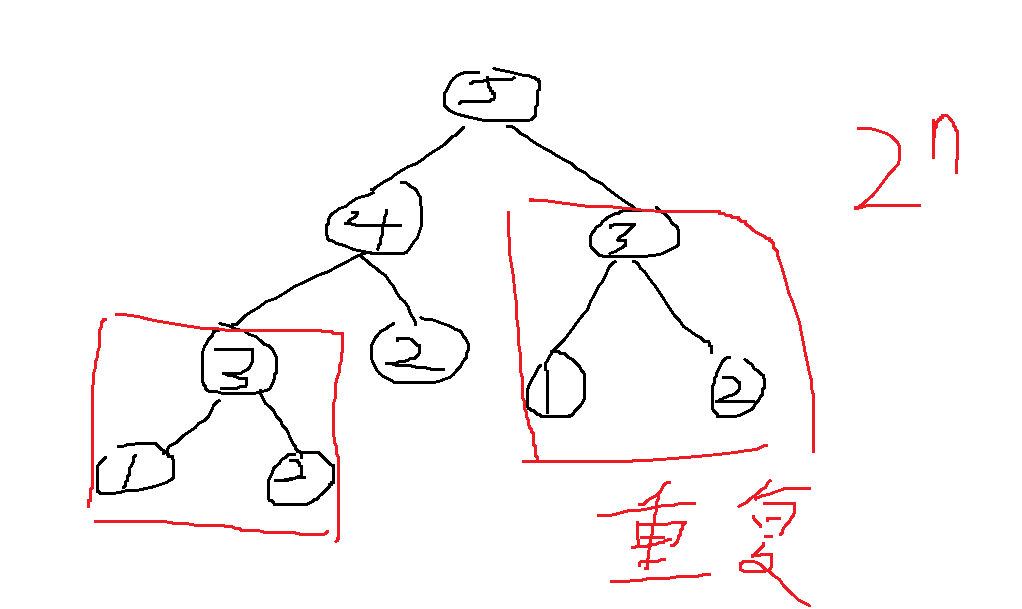
821. 跳台阶-记忆化搜索.png

写法1：返回前使用数组保存一下

#include<iostream>
using namespace std;

const int N = 20;

int n, mem[N];

int dfs(int u)
{
    if(mem[u] != 0) return mem[u];

    if(u == 1)
    {
        mem[1] = 1;
        return mem[1];
    }
    if(u == 2)
    {
        mem[2] = 2;
        return mem[2];
    }

    mem[u] = dfs(u - 1) + dfs(u - 2);
    return mem[u];

}

int main()
{
    scanf("%d", &n);
    cout << dfs(n);
    return 0;
}

写法2：类似于dfs 每个结点都有自己的信息要返回，使用局部变量

#include<iostream>
using namespace std;

const int N = 20;

int n, mem[N];

int dfs(int u)
{
    if(mem[u] != 0) return mem[u];

    int sum = 0;
    if(u == 1) sum = 1;
    else if(u == 2) sum = 2;
    else sum = dfs(u - 1) + dfs(u - 2);

    mem[u] = sum;
    return sum;

}

int main()
{
    scanf("%d", &n);
    cout << dfs(n);
    return 0;
}

对递归的分析
1、递归的过程：只有“归”的过程才是产生答案的过程（从下往上），边界为最小子问题的答案，要求已知
2、“递”的过程是分解子问题的过程（从上往下）

思考：有前面分析，只有在递归的过程中只有“归”的过程才会产生答案，那么只要“归”可不可以呢？
已知最小子问题的解，逐个递推求解！！！

#include<iostream>
using namespace std;

const int N = 20;

int n, f[N];


int main()
{
    scanf("%d", &n);

    f[1] = 1, f[2] = 2;
    if(n == 1 || n == 2) 
    {
        cout << f[n];
        return 0;
    }
    for(int i = 3; i <= n ;i++)
    {
        f[i] = f[i - 1] + f[i - 2];//这个递推公式就是 递归的 向下递归的公式dfs(u) = dfs(u - 1) + dfs(u - 2)
    }
    cout << f[n];
    return 0;
}

对比递归和dp的参数(错误理解xxxxxx)
1、递归：传参是最大值（最大问题的状态表示）(以下代码，递归传参为0，应该注重递归式，下面1049. 大盗阿福，也传的最小值)
2、dp：初始化最小值（最小子问题的状态表示）

#include<iostream>
using namespace std;

const int N = 20;

int n, f[N];

int dfs(int u)
{
    if(u == n) return 1;
    if(u > n) return 0;
    return dfs(u + 1) + dfs(u + 2);
}

int main()
{
    scanf("%d", &n);

    cout << dfs(0) << endl;


    return 0;
}

总结
1、暴力递归 -> 记忆化搜索 -> 递推（dp）
2、记忆化搜索 = 暴力递归 + 记录答案
3、dp的公式 = 向下递归的公式
4、dp数组的初始值 = 递归的边界

dp进一步优化 - 状态压缩(只用到三个变量，用来优化空间)

    //状态压缩
    int newf = 0, tmp1 = 1, tmp2 = 2;
    for(int i = 3; i <= n; i++)
    {
        newf = tmp1 + tmp2;
        tmp1 = tmp2;
        tmp2 = newf;
    }
    cout << newf;

+++++++++++++++
-1049. 大盗阿福
题目分析：今晚最多可以得到多少现金？ – 如果最后还能洗劫一家店，且不惊动警察，那么一定会去洗劫

dfs(深搜每一种情况，取最大值)
1、dfs(int u, int sum)//对第u家店铺进行选择，sum为此前已经偷的金额（类似于走台阶，选择一步还是两步，只是从上往下维护了一个参数（自动回溯））
2、针对的是选择u是否偷
3、O（2^n）– 超时

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 5;

int T, n;
int w[N];
int Max;

void dfs(int u, int sum)//对第u家店铺进行选择，sum为此前已经偷的金额
{
    if(u > n)
    {
        Max = max(Max, sum);
        return;
    }


    dfs(u + 2, sum + w[u]);//只要这个被偷过，那么下次一定会跳一个

    dfs(u + 1, sum);//选择不偷
}

int main()
{
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &w[i]);
        }
        Max = 0;
        dfs(1, 0);
        cout << Max << endl;

    }
    return 0;
}

递归O（2^n）(其实与dfs没有本质的区别，思想是一样的，理解起来不太一样，递归注重大问题分解为子问题，而dfs注重寻找方案数类似于人的选择，还有就是一个带返回值一个不带返回值)

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 5;

int T, n;
int w[N];

int dfs(int u)//递归写法
{
    if(u > n) return 0;//注意理解
    else return max(dfs(u + 1),dfs(u + 2) + w[u]);
}

int main()
{
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &w[i]);
        }

        cout << dfs(1) << endl;

    }
    return 0;
}

要想实现记忆化搜索那么递归的参数就需要尽可能少
记忆化搜索的本质就是如果递归的参数相同，那么对其进行保存，防止重复调用。言外之意递归的参数个数 = 记忆化数组的维数！！！
同时，没必要把影响到递归边界的参数放进来
如在本题中加入一个记录 当前洗劫的价值*

int dfs(int u, int cur_sum)
{
    if(u > n) return 0;
    else return max(dfs(u + 1, cur_sum), dfs(u + 2, cur_sum + w[u));
}

想要实现剪枝，那就需要尽可能的把剪枝时用的相关信息传到参数位置

权衡记忆化搜索和剪枝，都是优化的方式，但在参数数量上两者有一定的矛盾–权衡利弊

记忆化搜索实现(或者，直接先保存再返回，更容易理解)
mem[i]:从第i个店铺开始（i~n）能洗劫的最大价值

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 5;

int T, n;
int w[N];
int mem[N];

int dfs(int u)//递归写法
{
    if(mem[u]) return mem[u];

    int sum = 0;
    if(u > n) sum = 0;
    else sum = max(dfs(u + 1), dfs(u + 2) + w[u]);

    mem[u] = sum;
    return sum;
}

int main()
{
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &w[i]);
        }
        memset(mem, 0, sizeof mem);
        cout << dfs(1) << endl;

    }
    return 0;
}

#include<iostream>
#include<cstring>
using namespace std;

const int N = 1e5 + 5;

int T, n;
int f[N];
int w[N];

// int dfs(int u)//递归写法
// {
//     if(mem[u]) return mem[u];

//     int sum = 0;
//     if(u > n) sum = 0;
//     else sum = max(dfs(u + 1), dfs(u + 2) + w[u]);

//     mem[u] = sum;
//     return sum;
// }

int main()
{
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%d", &w[i]);
        }
        memset(f, 0, sizeof f);//边界都是0
        for(int i = n; i >= 1; i--)//注意是 倒序 ，即“归”的过程
        {
            f[i] = max(f[i + 1], f[i + 2] + w[i]); //对比记忆化搜索的 dfs(u) = max(dfs(u + 1), dfs(u + 2) + w[u])
        }

        cout << f[1] << endl;
    }
    return 0;
}

注意亦可以正序遍历，相当于倒叙递归dfs（n）参数为n
注意边界问题

for(int i = 1; i <= n; i++)
{
    f[i] = max(f[i - 1], f[i - 2] + w[i])
}
cout << f[n];

如果越界，可以下标同时 + 2(或者都 + 1，因为只会访问到 -1) w[i]不变 – 下标便宜操作

for(int i = 1; i <= n; i++)
{
    f[i + 2] = max(f[i + 1], f[i] + w[i]);
}
cout << f[n + 2];

同样可以状态压缩（三个变量） 注意转化的顺序小下表 = 大下标

int newf = 0, tmp1 = 0, tmp2 = 0;
for(int i = 1; i <= n; i++)
{
    newf = max(tmp1, tmp2 + w[i]);


    tmp2 = tmp1;// i - 2 = i - 1
    tmp1 = newf;i - 1 = i
}
cout << newf << endl;

总结：递归 - 记忆化搜索（空间换时间） - dp（倒序）- dp（正序 + 下标偏移） - 空间优化

==========================================================================================================
-898. 数字三角形

dfs（遍历所有方案）O（2^n）超时

#include<iostream>
using namespace std;

const int N = 510;

int n;
int g[N][N];
int Max = -10000 * 500;//注意数据范围

void dfs(int a, int b, int sum)//（a, b）当前坐标, 通过a和b可以算出当前所在行数 a+b-1 = u , sum:此前已有的和
{
    if(a + b - 1 > n)
    {
        Max = max(sum, Max);
        return;
    }

    dfs(a, b + 1, sum + g[a][b]);
    dfs(a + 1, b, sum + g[a][b]);

}

int main()
{
    scanf("%d", &n);

    //↙为行， ↘为列
    //寻找坐标和每行横纵坐标的关系
    for(int k = 2; k <= n + 1; k++)//每一行x + y的和不变
    {
        for(int i = 1; i <= k - 1; i++)
        {
            scanf("%d", &g[i][k - i]);
        }
    }

    dfs(1, 1, 0);

    cout << Max << endl;

    return 0;
}

递归 O(2^n)

总结
1、最优子问题：dfs(x) = max/min(dfs(a), dfs(b))
2、子问题的和：dfs(x) = dfs(a) + dfs(b)

#include<iostream>
using namespace std;

const int N = 510;

int n;
int g[N][N];
int Max;

int dfs(int a, int b)
{
    if(a + b - 1 > n) return 0;//边界都是0
    else return max(dfs(a, b + 1), dfs(a + 1, b)) + g[a][b];
}

int main()
{
    scanf("%d", &n);

    //↙为行， ↘为列
    //寻找坐标和每行横纵坐标的关系
    for(int k = 2; k <= n + 1; k++)//每一行x + y的和不变
    {
        for(int i = 1; i <= k - 1; i++)
        {
            scanf("%d", &g[i][k - i]);
        }
    }

    cout << dfs(1, 1);

    return 0;
}

记忆化搜索

#include<iostream>
using namespace std;

const int N = 510;

int n;
int g[N][N], mem[N][N];
int Max;

int dfs(int a, int b)
{
    if(mem[a][b]) return mem[a][b];

    int sum = 0;
    if(a + b - 1 > n) sum = 0;//边界都是0
    else sum = max(dfs(a, b + 1), dfs(a + 1, b)) + g[a][b];

    mem[a][b] = sum;
    return sum;
}

int main()
{
    scanf("%d", &n);

    //↙为行， ↘为列
    //寻找坐标和每行横纵坐标的关系
    for(int k = 2; k <= n + 1; k++)//每一行x + y的和不变
    {
        for(int i = 1; i <= k - 1; i++)
        {
            scanf("%d", &g[i][k - i]);
        }
    }

    cout << dfs(1, 1);

    return 0;
}

输入方式1(↙为行， ↘为列)：dp(正序边界问题待解决) O(n^2)
注意：此时的倒序只有一个最终状态而且边界不需要处理，是0即可。 - 而正序，三角顶如果有负数，边界为0，会有错误的结果，而且最后的答案是三角底所有的状态，需要再找一次最大值

#include<iostream>
using namespace std;

const int N = 510, Min = -0x3f3f3f3f;

int n;
int g[N][N];
int f[N][N];



int main()
{
    scanf("%d", &n);

    //↙为行， ↘为列
    //寻找坐标和每行横纵坐标的关系
    for(int k = 2; k <= n + 1; k++)//每一行x + y的和不变
    {
        for(int i = 1; i <= k - 1; i++)
        {
            scanf("%d", &g[i][k - i]);
        }
    }

    //倒序
    //边界都是0
    for(int i = n; i >= 1; i--)
    {
        for(int j = n; j >= 1; j--)
        {
            f[i][j] = max(f[i][j + 1], f[i + 1][j]) + g[i][j];
        }
    }
    cout << f[1][1];


    //正序(到最后是n个状态，三角形底部，所有求最值)
    //下标边界是0，不用偏移(但是如果有值的地方是负数，那么边界0会有影响)
    // for(int j = 1; j <= n; j++)
    // {
    //     f[0][j] = -10000;
    //     f[j][0] = -10000;
    // }
    // f[1][1] = g[1][1];
    // for(int i = 1; i <= n; i++)
    // {
    //     for(int j = 1; j <= n; j++)
    //     {
    //         f[i][j] = max(f[i - 1][j], f[i][j - 1]) + g[i][j];
    //     }
    // }

    // for(int k = 2; k <= n + 1; k++)//每一行x + y的和不变
    // {
    //     for(int i = 2; i <= k - 1; i++)
    //     {
    //         cout << f[i][k - i] << " ";
    //     }
    //     cout << endl;
    // }
    // int Max = -10000 * 500;//注意数据范围， 最小值
    // //参照输入的规律k = n + 1;
    // for(int j = 1; j <= (n + 1) - 1; j++)
    // {
    //     cout << f[j][(n + 1) - j] << " " << endl;
    //     // Max = max(Max, f[j][(n + 1) - j]);
    // }
    // cout << Max;


    return 0;
}

输入方式2(正常输入)： dp
注意：
1、正序边界特判
2、二维优化到一维（目前不太懂）

#include<iostream>
using namespace std;

const int N = 510;

int n;
int g[N][N];
// int f[N][N];
int f[N];

int main()
{
    scanf("%d", &n);

    for(int i = 1; i <= n; i++)//没必要找规律，怎么输入怎么来
    {
        for(int j = 1; j <= i; j++)
        {
            scanf("%d", &g[i][j]);
        }
    }

    //倒序
    for(int i = n; i >= 1; i--)
    {
        for(int j = 1; j <= i; j++)//j正序
        {
            // f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + g[i][j];
            f[j] = max(f[j], f[j + 1]) + g[i][j];//二维优化一维
        }
    }
    // cout << f[1][1];
    cout << f[1];

    // //正序(因为负数的存在注意边界)
    // f[1][1] = g[1][1];//第一个点特判
    // //其他边界变成最小值， 这样对路径和取最大，就没有影响了
    // for(int i = 1; i <= n; i++)
    // {
    //     f[i][0] = -10000 * 500;//左侧边界
    //     f[i][i + 1] = -10000 * 500;//右侧边界
    // }
    // for(int i = 2; i <= n; i++)
    // {
    //     for(int j = 1; j <= i; j++)
    //     {
    //         f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + g[i][j];
    //     }
    // }

    // int Max = -10000 * 500;
    // for(int j = 1; j <= n; j++)
    // {
    //     Max = max(Max, f[n][j]);
    // }
    // cout << Max;
    return 0;
}

=====================================================================
-01背包问题

dfs(暴力搜索每一种情况，维护最大值)O(2^n) 指数型枚举

#include<iostream>
using namespace std;

const int N = 1010;

int n, V;
int v[N], w[N];
int M_w;

void dfs(int u, int spv, int cur)//考虑第u个物品，当前已剩下的容量， 当前已有的价值总量
{
    if(u >= n + 1)
    {
        M_w = max(M_w, cur);
        return;
    }

    if(spv >= v[u])//容量还够, 可以选
    {
        dfs(u + 1, spv - v[u], cur + w[u]);
    }
    dfs(u + 1, spv, cur);//不选，但当容量不足时，只能不选

}

int main()
{
    scanf("%d%d", &n, &V);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &v[i], &w[i]);
    }

    dfs(1, V, 0);

    cout << M_w << endl;
    return 0;
}

递归 O（2^n）超时
1、带返回值，dfs(u, spv),返回从u开始考虑， u~n产生的最大价值（那么当u > n时的边界问题就清楚为什么 return 0）
2、返回值即为最大价值（u~n），少一参数，方便后续记忆化搜索
3、最大子问题：
·当有多种选择的时候max、min
·但本题当spv < v[i]的时候只有一种选择，必须走

#include<iostream>
using namespace std;

const int N = 1010;

int n, V;
int v[N], w[N];


int dfs(int u, int spv)//注意返回值的含义
{
    if(u >= n + 1) return 0;//根据返回值理解


    if(spv < v[u])//只有不选的情况，必须走
    {
        return dfs(u + 1, spv);
    }
    else if(spv >= v[u])//多种选择，最值子问题
    {
        return max(dfs(u + 1, spv), dfs(u + 1, spv - v[u]) + w[u]);
    }

}
int main()
{
    scanf("%d%d", &n, &V);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &v[i], &w[i]);
    }

    cout << dfs(1, V) << endl;
    return 0;
}

记忆化搜索（在递归的基础上）（时间可）

#include<iostream>
using namespace std;

const int N = 1010;

int n, V;
int v[N], w[N];
int mem[N][N];

int dfs(int u, int spv)//注意返回值的含义
{
    if(mem[u][spv]) return mem[u][spv];//返回记忆
    if(u >= n + 1) return 0;//根据返回值理解

    int sum = 0;
    if(spv < v[u])//只有不选的情况，必须走
    {
        sum = dfs(u + 1, spv);
    }
    else if(spv >= v[u])//多种选择，最值子问题
    {
        sum = max(dfs(u + 1, spv), dfs(u + 1, spv - v[u]) + w[u]);
    }

    mem[u][spv] = sum;
    return mem[u][spv];
}
int main()
{
    scanf("%d%d", &n, &V);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &v[i], &w[i]);
    }

    cout << dfs(1, V) << endl;
    return 0;
}

dp
1、在递归的基础上改，递推式 == 递归的调用（两者的本质是相同的，都是状态转换）
2、本题递归当中分情况的递归调用，所以递推式也要分情况写\
3、注意递推时遍历的顺序，与归的顺序相同

#include<iostream>
using namespace std;

const int N = 1010;

int n, V;
int v[N], w[N];
int f[N][N];

// int dfs(int u, int spv)//注意返回值的含义
// {
//     if(mem[u][spv]) return mem[u][spv];//返回记忆
//     if(u >= n + 1) return 0;//根据返回值理解

//     int sum = 0;
//     if(spv < v[u])//只有不选的情况，必须走
//     {
//         sum = dfs(u + 1, spv);
//     }
//     else if(spv >= v[u])//多种选择，最值子问题
//     {
//         sum = max(dfs(u + 1, spv), dfs(u + 1, spv - v[u]) + w[u]);
//     }

//     mem[u][spv] = sum;
//     return mem[u][spv];
// }
int main()
{
    scanf("%d%d", &n, &V);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d", &v[i], &w[i]);
    }

    for(int i = n; i >= 1; i--)//与递顺序相反，与归的顺序相同
    {
        for(int spv = 0; spv <= V; spv++)//注意体积的顺序，与归的顺序相同
        {
            if(spv < v[i])
            {
                f[i][spv] = f[i + 1][spv];
            }
            else if(spv >= v[i])
            {
                f[i][spv] = max(f[i + 1][spv], f[i + 1][spv - v[i]] + w[i]);
            }
        }
    }

    cout << f[1][V];
    return 0;
}

=================================================================================
-1371. 货币系统
dfs(维护全局)
思路一：根据容量够不够分支，只能走一个分支（注意分支结构）

#include<iostream>
using namespace std;

const int N = 30;

int V, n;
int v[N];
long long num;

void dfs(int u, int spn)
{
    if(u > V)
    {
        if(spn == 0) num++;
        return;
    }

    if(spn < v[u])//不够，只能不选
    {
        dfs(u + 1, spn);
    }
    else if(spn >= v[u])//够，不选+选（选几个）
    {
        dfs(u + 1, spn);//不选

        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v)
            {
                break;
            }
            dfs(u + 1, spn - t_v);
        }

    }


}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    dfs(1, n);

    cout << num;

    return 0;
}

思路二：无论如何都有不选的权力，只有在容量够的时候才考虑选（选几个）
注意理解：（1）都走，（2）有容量走，（1）（2）在有容量时都走

#include<iostream>
using namespace std;

const int N = 30;

int V, n;
int v[N];
long long num;

void dfs(int u, int spn)
{
    if(u > V)
    {
        if(spn == 0) num++;
        return;
    }

    //(1)
    dfs(u + 1, spn);//无论如何都走
    //(2)
    if(spn >= v[u])//只有有容量时，才走
    {
        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v)
            {
                break;
            }
            dfs(u + 1, spn - t_v);
        }
    }


}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    dfs(1, n);

    cout << num;

    return 0;
}

递归(超时)

返回值：从第i个物品考虑，返回i~n的所有方案数 - 同dp状态的理解
思路1：同上

#include<iostream>
using namespace std;

const int N = 30;

int V, n;
int v[N];

long long dfs(int u, int spn)
{
    if(u > V)
    {
        if(spn == 0) return 1;
        else if(spn > 0) return 0;
    }

    if(spn < v[u])//只能不选
    {
        return dfs(u + 1, spn);
    }
    else if(spn >= v[u])//选（选几个）或不选
    {
        int sum = 0;
        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v)
            {
                break;
            }
            sum += dfs(u + 1, spn - t_v);
        }
        return dfs(u + 1, spn) + sum;//不选 + 选（几个）
    }
}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    cout << dfs(1, n);

    return 0;
}

思路二：同上

#include<iostream>
using namespace std;

const int N = 30;

int V, n;
int v[N];

long long dfs(int u, int spn)
{
    if(u > V)
    {
        if(spn == 0) return 1;
        else if(spn > 0) return 0;
    }

    long long num = 0;
    num += dfs(u + 1, spn);

    if(spn >= v[u])
    {
        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v) break;
            num += dfs(u + 1, spn - t_v);
        }
    }

    return num;
}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    cout << dfs(1, n);

    return 0;
}

记忆化搜索
思路一（10/13 超时）

#include<iostream>
using namespace std;

const int N = 30, M = 1e4 + 5;

int V, n;
int v[N];
long long  mem[N][M];

long long dfs(int u, int spn)
{
    if(mem[u][spn]) return mem[u][spn];
    if(u > V)
    {
        if(spn == 0) return 1;
        else if(spn > 0) return 0;
    }

    long long num = 0;
    if(spn < v[u])//只能不选
    {
        num += dfs(u + 1, spn);
    }
    else if(spn >= v[u])//选（选几个）或不选
    {
        long long sum = 0;
        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v)
            {
                break;
            }
            sum += dfs(u + 1, spn - t_v);
        }
        num += dfs(u + 1, spn) + sum;//不选 + 选（几个）
    }
    mem[u][spn] = num;
    return num;
}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    cout << dfs(1, n);

    return 0;
}

思路二（10/13 超时）

#include<iostream>
using namespace std;

const int N = 30, M = 1e4 + 5;

int V, n;
int v[N];
long long mem[N][M];

long long dfs(int u, int spn)
{
    if(mem[u][spn]) return mem[u][spn];
    if(u > V)
    {
        if(spn == 0) return 1;
        else if(spn > 0) return 0;
    }

    long long num = 0;
    num += dfs(u + 1, spn);

    if(spn >= v[u])
    {
        for(int k = 1; ; k++)
        {
            int t_v = k * v[u];
            if(spn < t_v) break;
            num += dfs(u + 1, spn - t_v);
        }
    }
    mem[u][spn] = num;
    return num;
}


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }

    cout << dfs(1, n);

    return 0;
}

dp
思路一

#include<iostream>
using namespace std;

const int N = 30, M = 1e4 + 5;

int V, n;
int v[N];
long long f[N][M];


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }


    //初始化
    f[V + 1][0] = 1;//递归的边界条件，其他默认是 0
    //与 归 的顺序相同
    for(int i = V; i >= 1; i--)
    {
        for(int j = 0; j <= n; j++)
        {
            if(j < v[i])//不够
            {
                f[i][j] = f[i + 1][j];
            }
            else if(j >= v[i])//够
            {
                f[i][j] = f[i + 1][j];
                for(int k = 1; ; k++)
                {
                    int t_v = k * v[i];
                    if(j < t_v) break;
                    f[i][j] += f[i + 1][j - t_v];
                }
            }
        }
    }

    cout << f[1][n];

    return 0;
}

思路二（在思路一的基础上相当于把不选提公因式提出来了）

#include<iostream>
using namespace std;

const int N = 30, M = 1e4 + 5;

int V, n;
int v[N];
long long f[N][M];


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }


    //初始化
    f[V + 1][0] = 1;//递归的边界条件，其他默认是 0
    //与 归 的顺序相同
    for(int i = V; i >= 1; i--)
    {
        for(int j = 0; j <= n; j++)
        {
            f[i][j] = f[i + 1][j];//都走

            if(j >= v[i])//有容量时走
            {
                for(int k = 1; ; k++)
                {
                    int t_v = k * v[i];
                    if(j < t_v) break;
                    f[i][j] += f[i + 1][j - t_v];
                }
            }
        }
    }

    cout << f[1][n];

    return 0;
}

进一步简化代码
注意：k的范围，尤其k == 0时

#include<iostream>
using namespace std;

const int N = 30, M = 1e4 + 5;

int V, n;
int v[N];
long long f[N][M];


int main()
{
    scanf("%d%d", &V, &n);
    for(int i = 1; i <= V; i++)
    {
        scanf("%d", &v[i]);
    }


    //初始化
    f[V + 1][0] = 1;//递归的边界条件，其他默认是 0
    //与 归 的顺序相同
    for(int i = V; i >= 1; i--)
    {
        for(int j = 0; j <= n; j++)
        {
            for(int k = 0; k * v[i] <= j; k++)
            {
                f[i][j] += f[i + 1][j - k * v[i]];
            }
        }
    }

    cout << f[1][n];

    return 0;
}

=============================================================================
-312. 乌龟棋
递归（类似于dfs 搜索方案）（2/10）
返回值：返回从第i个格子开始走到终点的最高得分数

#include<iostream>
using namespace std;

const int N = 360, M = 130;

int n, m;
int se[N], cd[M];
bool st[M];//卡牌只能使用一次

int dfs(int u)
{
    if(u > n) return 0;
    if(u == n) return se[n];

    int t_max = 0;//记录分别选择五种卡片的最值
    for(int i = 1; i <= m; i++)
    {
        if(st[i]) continue;//卡牌已被使用

        st[i] = 1;
        t_max = max(t_max, dfs(u + cd[i]) + se[u]);//包括当前位置
        st[i] = 0;
    }

    return t_max;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &se[i]);
    }
    for(int i = 1; i <= m; i++)
    {
        scanf("%d", &cd[i]);
    }

    cout << dfs(1);

    return 0;
}

记忆化(在递归的基础上修改，但是测试样例过不了)
新的理解：记忆化搜索适用于具有重叠子问题的问题，即在不同的递归路径中会重复计算相同的状态。
此题：不同的搜索路径可能会导致到达相同位置时所使用的卡牌顺序不同，因此这两个状态是不同的，并不是重复子问题。给根据返回值的理解，从起点开始跳，和从第i个方块开始跳，状态并不一样（如果说，从第i个格子开始跳，牌的选择也可以刷新的话，那么才算相同的子问题）

#include<iostream>
#include<cstring>
using namespace std;

const int N = 360, M = 130;

int n, m;
int se[N], cd[M];
bool st[M];//卡牌只能使用一次
int mem[N];//记忆数组

int dfs(int u)
{

    if(mem[u] != -1) return mem[u];

    if(u > n) return 0;
    if(u == n) return se[n];

    int t_max = 0;//记录分别选择五种卡片的最值
    for(int i = 1; i <= m; i++)
    {
        if(st[i]) continue;//卡牌已被使用

        st[i] = 1;
        t_max = max(t_max, dfs(u + cd[i]) + se[u]);//包括当前位置
        st[i] = 0;
    }

    mem[u] = t_max;
    return t_max;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &se[i]);
    }
    for(int i = 1; i <= m; i++)
    {
        scanf("%d", &cd[i]);
    }

    memset(mem, -1, sizeof mem);
    cout << dfs(1);

    return 0;
}

dp（这种形式的递归，目前不会改成递推式）

0 评论

App 内打开

入门：递归（递 与 归）（与dfs的区别） - 记忆化搜索 （递归 + 记忆 目的减少重复子问题）-dp（相比递归 只有 归）

0 评论

入门：递归（递与归）（与dfs的区别） - 记忆化搜索（递归 + 记忆目的减少重复子问题）-dp（相比递归只有归）