开局一图：

先看一下最小生成树的定义

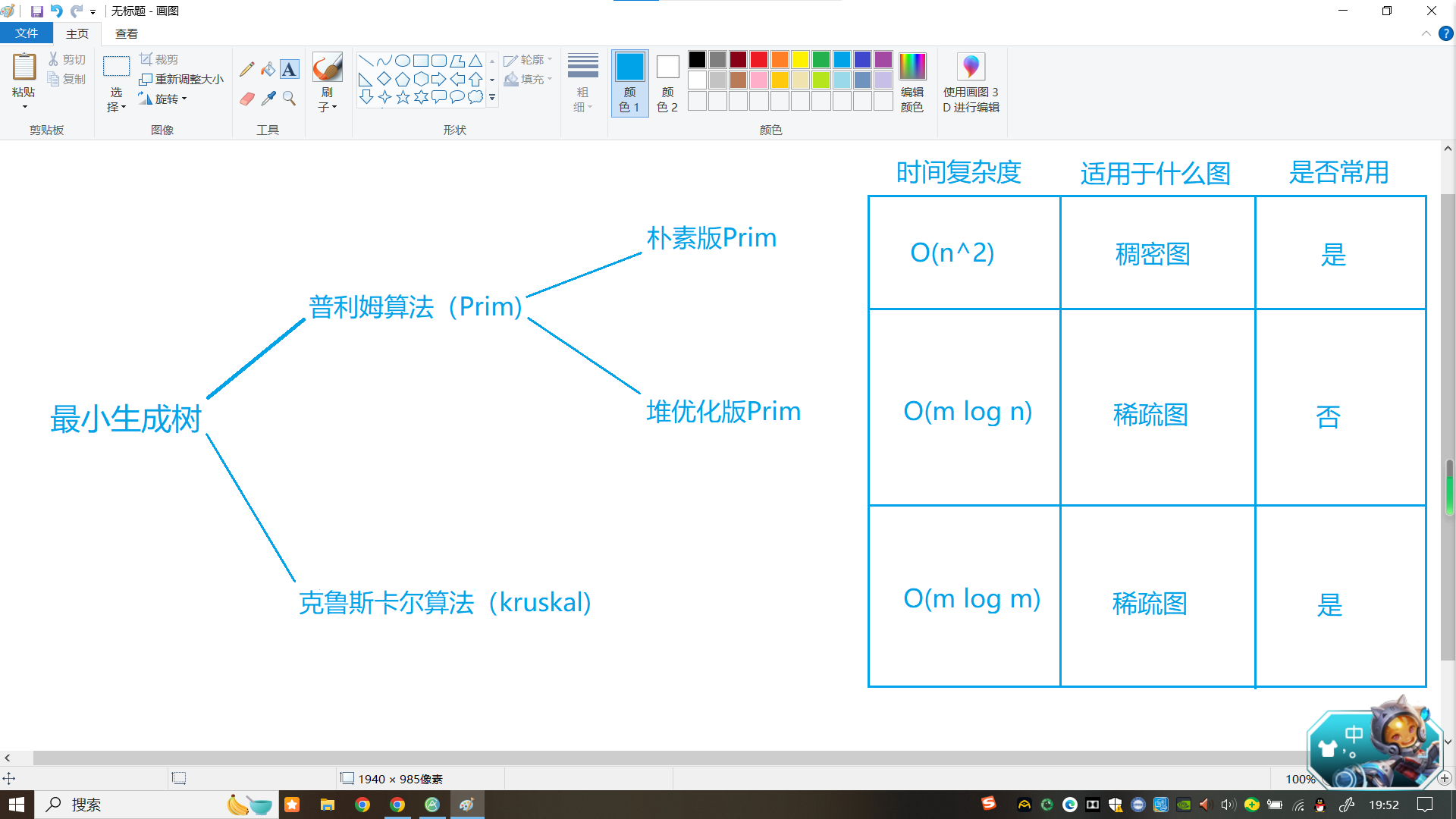
从上到下依次讲：

朴素版Prim算法：

第一步：先把所有距离初始化成正无穷

第二步：迭代$n$次，执行以下步骤：

1. 找到不在集合里面距离最近的点$t$，集合里存的是在最小生成树里面的点。
2. 用$t$更新其他点到集合的距离。

其实也就跟朴素版Dijkstra算法差不多，一些细节也一样，所以不用讲太细，不信回去看。
最常见的题差不多就是在一些城市之间铺公路，然后要所有城市联通，问最少费用是多少。

Look 这道题
是一个稠密图，从刚开始的图来看用Prim最适合。

代码：

int prim(){
    memset(dist, 0x3f, sizeof dist);
    int res = 0;
    for (int i = 0; i < n; i++){
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        if (i && dist[t] == INF) return INF;
        if (i) res += dist[t];
        st[t] = true;
        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

堆优化版Prim算法：

跟Dijkstra差不多，用堆来模拟。
一般考试时不会用，因为代码比较长，思路也没有Kruskal算法简单。

Kruskal算法：

第一步：将所有边按权重从小到大排序排序。

第二步：枚举每条边$a, b$权重为$c$。

如果$a, b$不联通，就把他加到集合里面去。而这一步可以用并查集。

代码：

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}