题目描述

有一长方形，长为 343720 单位长度，宽为 233333 单位长度。在其内部左上角顶点有一小球（无视其体积），其初速度如图所示且保持运动速率不变，分解到长宽两个方向上的速率之比为 dx : dy = 15 :17。小球碰到长方形的边框时会发生反弹，每次反弹的入射角与反射角相等，因此小球会改变方向且保持速率不变（如果小球刚好射向角落，则按入射方向原路返回）。从小球出发到其第一次回到左上角顶点这段时间里，小球运动的路程为多少单位长度？答案四舍五入保留两位小数。

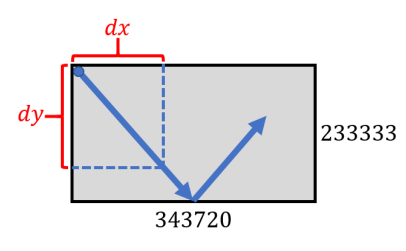
分析

学过物理的应该知道，我们分析一个小球在二维平面上的运动时，可以把它分解为x方向上的运动以及y方向上的运动。由题意可知，小球在x方向上单位时间的运动为dx，在y方向上单位时间的运动为dy。立即推，当小球回到原点的时候，小球在x方向上的路程以及y方向上的路程在边长的mod 2意义下是0的（也就是一定是相应边长的偶数倍才能回到原点）：
$$s_x\equiv 0 (mod\ 2l)\tag{1}$$
$$s_y\equiv 0 (mod\ 2w)\tag{2}$$
上式中$w$表示长方形的宽，$l$表示长方形的长度。
根据小学二年级的物理知识，路程是时间和速度的乘积:
$$s_x = dx\times t\tag{3}$$
$$s_y = dy\times t\tag{4}$$
根据前面的叙述，我们不妨假设$s_x=a\times l,s_y = b\times w$，其中$a,b$均为整数。由(1)(2)可知，$a$和$b$均为2的倍数。
将(3)(4)两个式子作比值就可以消去时间$t$:
$$\frac{s_x}{s_y} = \frac{a\times l}{b\times w} =\frac{d_x}{d_y}=\frac{15}{17}\tag{5}$$
对(5)进行化简，去掉分数形式后，可以得到
$$17a\times l=15b\times w\tag{6}$$

暴力搜索满足(6)的答案即可。

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;

int main()
{
    long long w = 233333;
    long long l = 343720;
    for(long long x = 0; x <= 10000; x ++)
    {
        for(long long y = 0; y <= 10000; y ++)
        {
            // 偶数 && 均不为 0
            if(15 * w * y == 17 * l * x && x % 2 == 0 && y % 2 == 0 && x != 0 && y != 0)
            {
                cout << x << " " << y << endl;
                double res = sqrt((l * x) * (l * x) + (w * y) * (w * y));
                printf("%llf", res);
                return 0;
            }
        }
    }

    return 0;
}