快速幂:
// cpp
while (m -- ){
if (m & 1) res = res * 2; //可以加上 % MOD, 注:MOD是模,一个数,%是取模运算. 这一行就是二分到最后如果奇数还剩一个2,就给答案乘上去。
else{
m >>= 1; //如果是偶数,
res = res * res; //则二分逆向叠积上去 比如// 2^16 = (2^8)*(2^8) = (2^4)*2^4*再来一遍= (2^2)*(2^2)*再来一遍*再来多一遍=4*4*...=(16*16)*(16*16)=256*256=65536, 也就只算了一半的数,而且循环递归次数很少
}
}
// Java:
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(); // 读入下一个整数
int res = 1;
while (m-- > 0 ){
if ((m & 1) != 0) res = res * 2; //可以加上 % MOD, 注:MOD是模,一个数,%是取模运算
else{
m >>= 1;
res = res * res;
}
}
System.out.println(res);
}
后续慢慢更新
数据结构:
1. 构造图和无环联通图:树Tree
数组手动实现邻接链表,矩阵。(邻接表/邻接矩阵实现稀疏图和稠密图的构建),如果图里空的点老多了,那就一条一条邻接表来画图效率高些,否则邻接矩阵直观些.
由于就两种:无向图和有向图a->b. 无向图双向建一下即可,所以都当成有向图处理。
1. 邻接表:$O(n)$
// head头,e当前节点, ne即next节点(被谁指过来的比如a->b, b的ne就是a, h[a]),节点a所到的边存在链表, 即h[a].next。
// 板子默认往头插入,也就是说next反着的.
int h[N], e[N], ne[N], idx;
void add(a, b){
e[idx] = b, ne[idx] = h[a], h[a]= idx++;
//当前点b 存到当前idx=0上。next点(前一个点)是a, 随后插入完成, 序号往后移动一位。 所以idx=0 开始的话,h[a]应初始化为-1, 因为插一次后h[a]=0,1,2,3... (插多次)
}
- 邻接矩阵 g[a][b] 存储边a->b (二维数组)$O(n^2)$
2. 链表
- 数组实现单链表
- 结构体实现单链表
3. 并查集,
就是把两颗树连在了一起,变成一个联通的块
4. 树,二叉树,各种树
ref: 基础课 https://www.acwing.com/file_system/file/content/whole/index/content/4800/
1:20:00左右
。。。其他
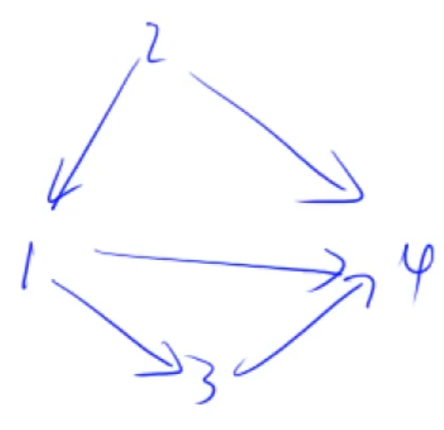
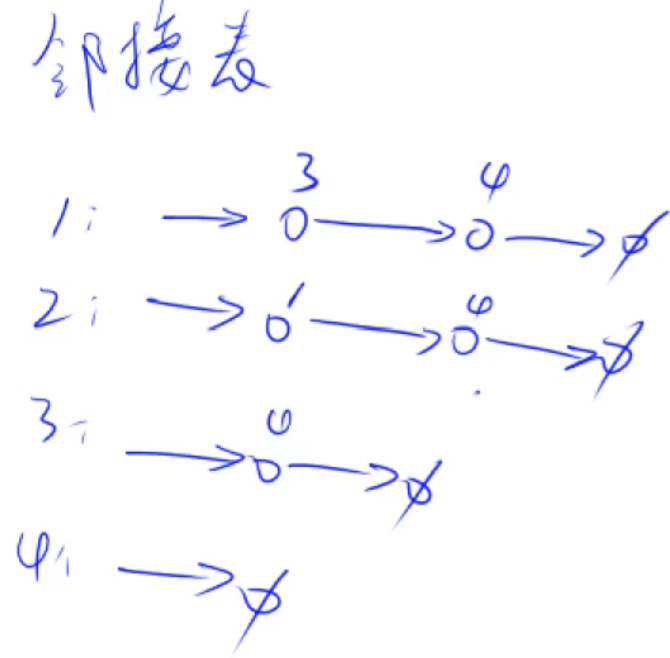
$\color{pink}{邻接表原理}$
h[1] -> 3 ->4 ->空集 (3,4顺序无所谓,都是第idx个节点相连边的链表的.
h[2] -> 1 -> 4 -> 空集
比如插一条2->3
h[2]->3->1->4->空集. 3->1, h[2]->3
h[3] -> 4 -> 空集
h[4] -> 空集
/*
h[N] : 表示 第 i 个节点的 第一条边的 idx
ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
e[M] : 表示 第idx 条边的 终点
N : 节点数量
M:边的数量
i : 节点的下标索引
idx : 边的下标索引
h[2]->1->4->空
add(2,3)
idx 即插入的第几条边。第一条2->4 e[0] = 4, ne[0] = h[2]=-1, h[2]=1; (原本空的h[2]=-1,这样每次加一条边,头节点都向后一位, -1, 1,2,3,4...)
第三条边2->3, e[2] = 3, ne[2] = 3, h[2] = 3;(第四条再插就往idx=3插,e[3],ne[3],...)
ne存的是头节点的下标哦,它的下一个(前面那个节点)是第几号.ne 从-1到0到1...到n-2 一共n个节点,n-1条边。
//n个头节点全部初始化,选个-1, 因为第一条边idx从0到1, h[2]从-1到0,到后面1,2,3刚好间隔1. 且idx从0开始.
*/
留空下面写代码

