建议收藏，文章超长；制作不易，不喜勿喷；点赞收藏过10周更，过30日更。（

本文涉及大量基础算法，会有link来告诉大家以前的位置

n锅端行动现在开始。

树状数组

朴素树状数组

这个东西很好写，但支持的操作比较少，就很难受。

树状数组涉及一些二进制的东西，具体可以看看lowbit运算。

证明不多说了吧。

然后开始遨游数据结构吧！

先准备好一个数组：

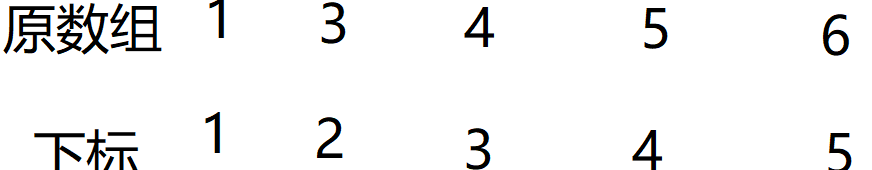
什么是树状数组呢？

他可以快速的维护区间和，跑的飞快，代码很短。

先来看一下树状数组的表示形式：

$$ C_1 = A_1\\\ C_2 = A_1 + A_2\\\ C_3 = A_2\\\ C_4 = A_1 + A_2 + A_3 + A_4 \\\ \ldots\\\ $$

接着我们用形象的图片来表示一下吧。

引用一个经典的例子。

我们把树状数组建立的过程想象成爬楼梯。

首先，$C_1$建立了一个梯子，到达了高度为一的地方。

接着$C_2$在$C_1$的基础上继续爪巴，然后到达了高度为二的地方。

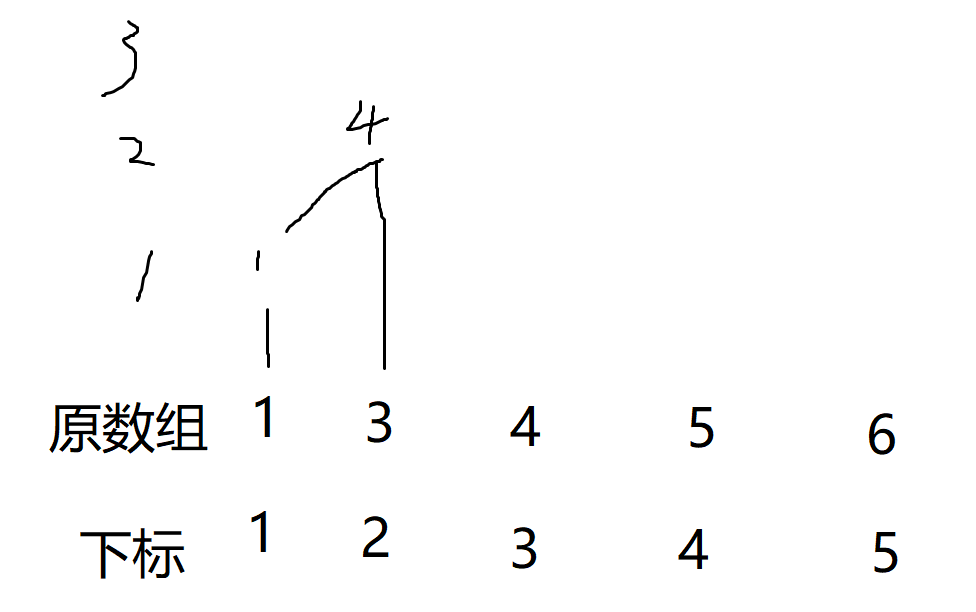
于是大家越爬越高。最后建成的这个类似于数树的东西就是树状数组了！！

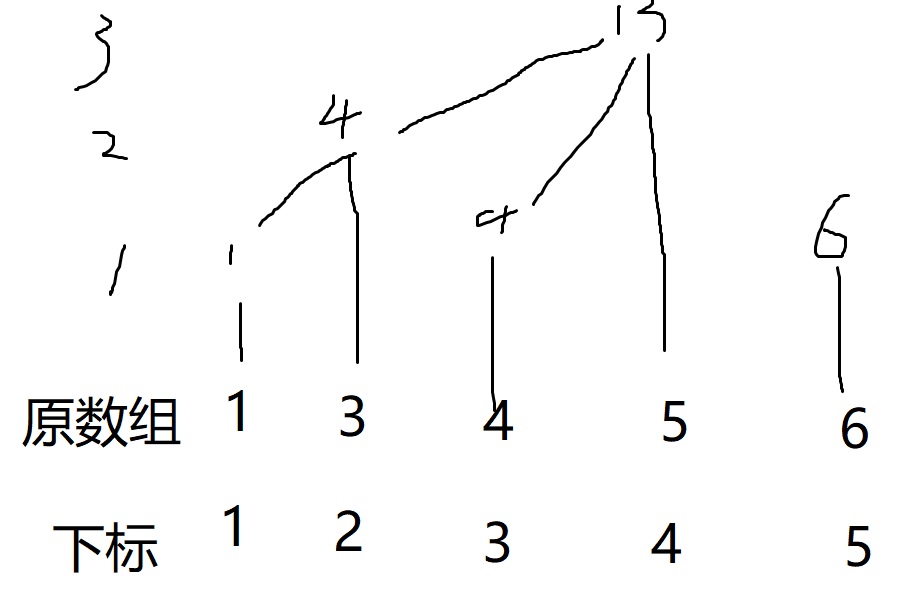
这个数组中的区间和如下图所示：

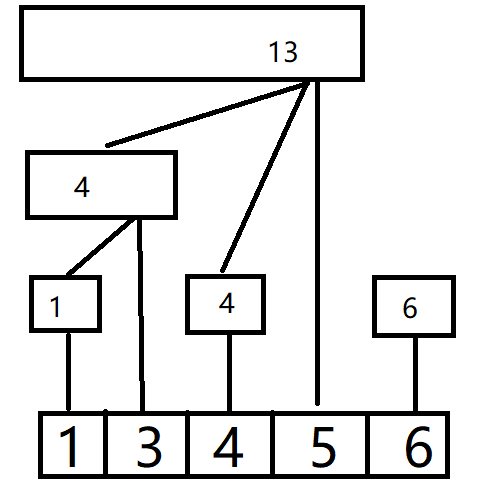
那么我们先来思考一下这个数组可以不可以算出所有的区间和。

我们发现，其实每一段的区间和都可以用这些加加减减来凑出来。所以说真的很妙啊！

接着我们来观察一下什么性质。我们先把每个数都转化为二进制。

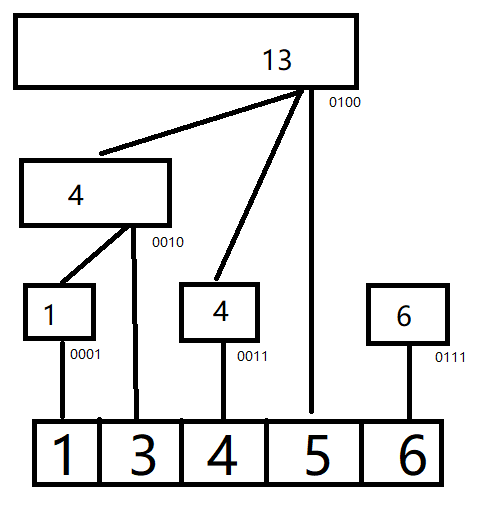
接着我们观察可以发现，对于树状数组上的$x$做lowbit运算后得到的结果就是树状数组所覆盖的长度。

然后整个树的深度是$log n + 1$。

那么我们来看一下树状数组支持的操作吧！

最简单的树状数组可以支持单点修改，区间查询。

这个时候我们先单点间修改add操作，那么我们可以从最开始的那个点开始，不停的向上加loubit，找到上一层，然后再加。

代码如下：

void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c; 
}

然后我们来看区间查询操作。我们可以利用前缀和相减的思想，然后从查询的地方向上减去lowbit的结果，查询前缀和。

前缀和可以看这个

代码如下：

int sum(int x)
{
    int res=  0;
    for(int i = x; i ; i -= lowbit(i)) res += tr[i];
    return res;
}

这就是板子了。

我们来看看具体的题目吧。

楼兰图腾

这个题目还是比较妙的，我们发现按照暴力做法可以直接枚举，时间复杂度$O(N ^ 2)$。

然后的话，怎么来优化呢？仔细看一下，发现要想求两种图腾可以拆分开看。

这里只要使用树状数组求逆序对就行了。

我们可以先把他中间的那个点按照高度进行分类，最后再相加就行了。

然后问题就转化成了一个点的左边和右边有多少个点比它高或者比它矮。

然后我们预处理出来一个数字，表示$1$到$k-1$中多少个数比它大，然后再算右边，最后乘起来就行了。

那就是板子啦！

发过来的A也是一样的。

接下来是本题的代码，供大家参考一下：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010;
int n,a[N],tr[N],Greater[N],lower[N];
int lowbit(int x)
{
    return x & -x;
}
void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c; 
}
int sum(int x)
{
    int res=  0;
    for(int i = x; i ; i -= lowbit(i)) res += tr[i];
    return res;
}
int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        int y = a[i];
        Greater[i] = sum(n) - sum(y);
        lower[i] = sum(y - 1);
        add(y,1);
    }
    memset(tr,0,sizeof tr);
    LL res1 = 0,res2=0;
    for(int i = n;i;i--)
    {
        int y = a[i];
        res1 += Greater[i] * (LL)(sum(n) - sum(y));
        res2 += lower[i] * (LL)(sum(y - 1));
        add(y, 1);
    }
    cout << res1<<' ' << res2;
}

奇怪的变种树状数组

先来一道例题

一看就发现，诶，这怎么不太一样啊？

对了，我们刚才维护的是前缀和，可以区间查询，现在变成了要求区间修改，那么我们用什么呢？

这个可以用差分，忘记的话看看这个。

差分可以实现在两个点做变动就可以改变整个数组，这样的话树状数组就有救了。

具体的办法是在原数组上建立差分数组，因为原数组是差分数组的前缀和，所以可以实现单点查询。

小伙伴们都学会了吗？？

这告诉了我们一个道理：有些东西别硬钢，转换一下思路，也许题目就变简单了。

代码大家可以参考一下；

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010;
int n,m,a[N];
LL tr[N];
int lowbit(int x)
{
    return x & -x;
}
void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int sum(int x)
{
    int res = 0;
    for(int i = x;i;i -= lowbit(i)) res += tr[i];
    return res;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++) add(i, a[i] - a[i - 1]);
    while(m --)
    {
        char op[2];
        int l,r,d;
        cin >> op >> l;
        if(*op == 'C')
        {
            cin >> r >> d;
            add(l,d), add(r + 1, -d);
        }
        else{
            cout << sum(l) << endl;
        }
    }
}

更加奇怪的树状数组

神™简单的问题

首先一看，md，区间修改区间查询这不是线段树的事情吗？

别急，稍安勿躁，这里说一个树状数组处理这种问题的套路。

先说正常思路，非常难整，但还是简单说一下，虽然不常用。

就是开两个树状数组对区间分别进行维护，非常的难。

首先的话我们可以看出求出来很复杂。

开两个数组，然后b数组维护的前缀和在a数组中对应的是：

$$\sum_{i=1}^x \sum_{j=1}^i b[j] $$

然后进行亿点点转换，可以变成:

$$\sum_{i=1}^x \sum_{j=1}^i b[j] = \sum_{i=1}^x (x-i+1) \times b[i] = (x+1)\sum_{i=1}^x b[i] - \sum_{i=1}^x i \times b[i]$$

这样的话两个可以分别使用两个树状数组来进行维护，这样的话思路还是很妙的，然后还可以利用差分简化代码。

y总的代码挺长的，这里按照秦大佬的思路给出一份简短的代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) x&(-x)
const int N=2e5;
ll c1[N],c2[N],n,m,a[N];
ll add(ll x,ll y)
{
    for(ll i=x;i<=n;i+=lowbit(i))
    {
        c1[i]+=y;
        c2[i]+=x*y;
    }
}
ll ask(ll x)
{
    ll ans=0;
    for(ll i=x;i;i-=lowbit(i))
        ans+=(x+1)*c1[i]-c2[i];
    return ans;
}
int main()
{
    scanf("%lld%lld\n",&n,&m);
    for(ll i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        add(i,a[i]-a[i-1]);
    }
    getchar();
    while(m--)
    {
        char ch=getchar();
        if (ch=='Q')
        {
            ll x,y;
            scanf("%lld%lld\n",&x,&y);
            cout<<ask(y)-ask(x-1)<<endl;
        }
        if (ch=='C')
        {
            ll x,y,d;
            scanf("%lld%lld%lld\n",&x,&y,&d);
            add(x,d);
            add(y+1,-d);
        }
    }
    return 0;
}

作者：秦淮岸灯火阑珊
链接：https://www.acwing.com/solution/content/1011/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

当然正解是线段树，这个马上就说了。

自己做做吧，思考题

这个提示一下，可以结合二分的思想降低时间复杂度，然后利用楼兰图腾那题的思想求解。

然后就是线段树啦！

我是@cht

建议收藏，文章超长；制作不易，不喜勿喷；点赞收藏过10周更，过30日更。（

bye