动态规划(Dynamic Programming)
-
重叠子问题
✓子问题是原大问题的小版本,计算大问题的时候,需要多次重复计算小问题 -
最优子结构(最优化原理)
✓通过求解子问题的最优解,可以获得原问题的最优解 -
无后效性
✓某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响(未来与过去无关)
动态规划步骤:
-
定义状态(状态是原问题、子问题的解)
✓比如定义dp(i) 的含义 -
设置初始状态(边界)
✓比如设置dp(0) 的值 -
确定状态转移方程
✓比如确定dp(i) 和dp(i–1) 的关系
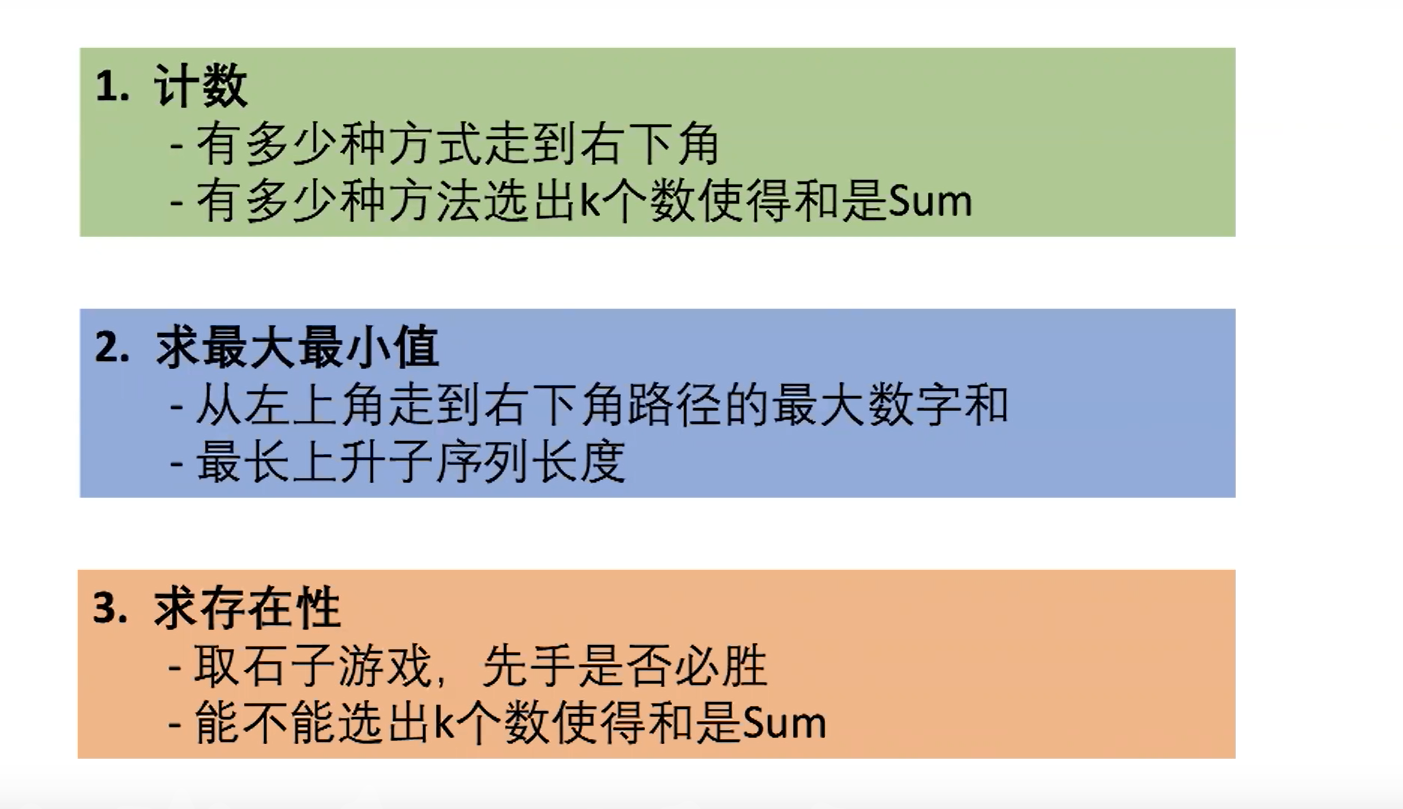
线性DP引入
最少硬币数量(没有数量限制) vs 最少硬币数量(有数量限制)
走迷宫(左上到右下)
状态转移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1];
注意起始边界赋值
摘花生(滚动数组)
!滚动数组(提高效率)在N很大的情况下可以达到压缩存储的作用
状态转移方程:f[i&1][j] = max(f[i&1][j-1], f[(i-1)&1][j]) + a[i&1][j];
被3整除的子序列
dp[i][j] 表示前 i 个长度的所有子序列数位数字和取模 3 为 j 的数目
不选:dp[i-1][j];
选:dp[i-1][(3+j-x)%3]
解释选择的情况:加上num恰巧等于j,即原来是j-num,
(j-num可能为负数,此时要加上余数再取余)
状态转移方程:dp[i][j]=(dp[i-1][j]+dp[i-1][(3+j-x)%3])%mod;
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
string str;
int dp[55][55];
int main()
{
cin>>str;
dp[1][(str[0]-'0')%3]=1;
int s=str.length();
for(int i=2;i<=s;i++)
{
int x=(str[i-1]-'0')%3;
for(int j=0;j<=2;j++)
{
dp[i][j]=(dp[i-1][j]+dp[i-1][(3+j-x)%3])%mod;
}
dp[i][x]=(dp[i][x]+1)%mod;
}
printf("%d\n",dp[s][0]%mod);
}
求子数组最大和
题意:输入的数组为[1, -2, 3, 10, -4, 7, 2, -5],和最大的子数组为3, 10, -4, 7, 2,因此输出为该子数组的和18
法一:前缀和+指针l
int main(){
int maxx= 0;
int n;cin >> n;
for(int i=1;i<=n;i++){
cin >> a[i];
sum[i] = sum[i-1]+a[i];//前缀和
maxx = max(maxx,sum[i]);
}
for(int i=1;i<=n;i++){
int l = 1;
while(l<=i){
if(sum[i]>maxx) maxx = sum[i];
sum[i]-=a[l++];
}
}
cout<<maxx<<endl;
}
法二:动态规划
int main(){
int n;cin >> n;
int maxx =0;
for(int i=1;i<=n;i++){
cin >> a[i];
if(i<2) dp[i] = a[i];
else dp[i] = max(dp[i-1]+a[i],a[i]);//选与不选
maxx = max(maxx,dp[i]);
}
cout<<maxx<<endl;
}
搬宿舍
关键:(初始化条件)
因为要比较大小,需要取较小值,所以应该初始化为一个极大值INF=0x3f3f3f3f;
当j == 0时,即在一对物品都没搬时,所需疲劳值应该是0,此时令f[i][j] = 0。
for(int i=0;i<=n;i++)
f[i][0] = 0;
题意:求最低疲劳度
思路:首先确定状态(f[i][j])搬i件物品j趟
搬两件物品一趟 (1种)
搬三件物品一趟 (2种)看有没有选择第三件物品,实际上是在搬两件物品基础上加 1;
状态方程:f[i][j]=min(f[i-2][j-1]+(a[i]-a[i-1])*(a[i]-a[i-1]),f[i-1][j]);
完整代码:
#include<bits/stdc++.h>
using namespace std;
const int INF= 0x3f3f3f3f;
int f[2020][2020];
int a[1010];
int main(){
int n,k;
while(cin>>n>>k){
memset(a,0,sizeof(a));
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
memset(f,INF,sizeof(f));//因为要比较最小值,所以先把f数组定义为无穷
for(int i=0;i<=n;i++) f[i][0]=0;//初始化的确定可以先看下面状态转移方程需要什么
for(int i=2;i<=n;i++){
for(int j=1;j*2<=i;j++){
f[i][j]=min(f[i-2][j-1]+(a[i]-a[i-1])*(a[i]-a[i-1]),f[i-1][j]);
}
}
cout<<f[n][k]<<endl;
}
return 0;
}
最少拦截系统 ~最长上升子序列
我的思路:8 389 207 155 300 299 170 158 65
需要两个拦截系统:389 207 155
300 299 170 158 65
我们可以发现 207 和 299 无论怎样都不可以在同一系统
那么该问题可以转化为最长上升序列问题
f[i] = 1
for j in range(1, i):
if a[j] < a[i]:
f[i] = max(f[i], f[j]+1)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n;
int w[N], f[N];
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> w[i];
int mx = 1; // 找出所计算的f[i]之中的最大值,边算边找
for (int i = 0; i < n; i++) {
f[i] = 1; // 设f[i]默认为1,找不到前面数字小于自己的时候就为1
for (int j = 0; j < i; j++) {
if (w[i] > w[j]) f[i] = max(f[i], f[j] + 1); // 前一个小于自己的数结尾的最大上升子序列加上自己,即+1
}
mx = max(mx, f[i]);
}
cout << mx << endl;
return 0;
}
最长公共子序列
dp[i][j] 表示str1的前i个元素组成的序列 和 str2的前j个元素序列的最长公共子序列的长度
#include <bits/stdc++.h>
using namespace std;
const int MAX=500;
int dp[MAX][MAX]={0};
int main()
{
int len1,len2;
string str1,str2;
while(cin>>str1>>str2)
{
len1=str1.length();
len2=str2.length();
for(int i=1;i<=len1;i++)
for(int j=1;j<=len2;j++)
//状态转移方程
if(str1[i-1]==str2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
cout<<dp[len1][len2]<<endl;
}
return 0;
}
区间dp模板
其中用了一个辅助变量len,它等于当前处理的区间[i,j]的长度。
dp[i][j]是大区间,它需要从小区间dp[i][k]和dp[k+1][j]转移而来,
所以应该先计算出小区间,才能根据小区间算出大区间。
len就起到了这个作用,从最小的区间len=2开始,此时区间[i,j]等于[i,i+1]
len=n,此时区间[i,j]等于[1,n]
for (int i = 1; i <= n; i++) {
dp[i][i] = 初始值
}
for (int len = 2; len <= n; len++) //区间长度
for (int i = 1; i + len - 1 <= n; i++) { //枚举起点
int j = i + len - 1; //区间终点
for (int k = i; k < j; k++) { //枚举分割点,构造状态转移方程
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
区间DP引入
石子合并
#include<bits/stdc++.h>
using namespace std;
const int N =310;
int s[N];
int dp[N][N];
const int INF=0x7fffffff;
int main(){
int n,a;cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
s[i]=s[i-1]+a;
}
for(int len=2;len<=n;len++){ //区间长度
for(int i=1;i+len-1<=n;i++){//枚举起点
int j=i+len-1; //定义终点
dp[i][j]=INF; //求最小值定义无穷
for(int k=i;k<j;k++) //枚举断点
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
}
}
cout<<dp[1][n]<<endl;
}
另一种记忆化dfs:
#include<bits/stdc++.h>
using namespace std;
const int N =310;
int s[N];
int dp[N][N];
const int INF=0x3f3f3f;
int dfs(int l,int r){
int &t=dp[l][r];
if(l==r) return 0;//构不成两堆不能合并
if(t!=INF) return t;//已经计算过了
for(int i=l;i<r;i++){
t=min(t,dfs(l,i)+dfs(i+1,r)+s[r]-s[l-1]);//记忆化dfs
}
return t;
}
int main()
{
int n,a;cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
s[i]=s[i-1]+a;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
dp[i][j]=INF;
}
cout<<dfs(1,n)<<endl;
}
环形石子合并
#include<bits/stdc++.h>
using namespace std;
int n;
int a[MAXN];
int g[MAXN][MAXN],f[MAXN][MAXN]; //最大和最小
int sum[MAXN];
int main(){
scanf("%d",&n);
for(int i =1;i<=n;i++){
scanf("%d",&a[i]);
a[n+i] = a[i]; //构造
}
for(int i=1;i<=2*n;i++){ //前缀和
sum[i] =sum[i-1] + a[i];
}
memset(g,0x3f,sizeof(g));
memset(f,-0x3f,sizeof(f));
for(int lena=1;lena<=n;lena++){
for(int l=1;l+lena-1 <=n*2;l++){
int r = l + lena -1;
if(l == r){
g[l][r] = f[l][r] = 0;
}
else {
for(int k = l;k < r;k++){
g[l][r] = min(g[l][r],g[l][k]+g[k+1][r] + (sum[r] - sum[l-1]));
f[l][r] = max(f[l][r],f[l][k]+f[k+1][r] + (sum[r] - sum[l-1]));
}
}
}
}
int maxn = -INF,minx = INF;
for(int i=1;i<=n;i++){ //看n种分割哪种最大和最小
minx = min(minx,g[i][i+n-1]);
maxn = max(maxn,f[i][i+n-1]);
}
printf("%d\n%d\n",minx,maxn);
return 0;
}

