A

int main()
{
    int d[] = {1, 0, 2, 3, 4, 5, 6, 7, 8, 9};
    int n; cin >> n;
    if(n > 10) cout <<"-1" << endl;
    else
    {
        for(int i = 0; i < n; i ++)
            cout << d[i];
        cout << endl;
    }
    return 0;

}

E
找这样的子串， 存在就输出子串，不存在就输出none

int main()
{
    int n; cin >> n;
    string s; cin >> s;

    map<char, int>m;
    char a;int x = 0;
    for(int i = 0; i < n; i ++)
    {
        m[s[i]] ++;
        if(m[s[i]] == 5)
        {
            a = s[i];
            x = i;
            break;
        }
    }//cout << x << endl;

    map<char, int>mp;
    char b; int y = 0;
    for(int i = x + 1; i < n; i ++)
    {
        mp[s[i]] ++;
        if(mp[s[i]] == 7)
        {
            b = s[i];
            y = i;
            break;
        }
    }//cout << y << endl;

    map<char, int>mm;
    char c; int z = 0;
    for(int i = y + 1; i < n; i ++)
    {
        mm[s[i]] ++;
        if(mm[s[i]] == 5)
        {
            z = i;
            c = s[i];
            break;
        }
    }//cout << z << endl;

    if(x && y && z)
    {
        for(int i = 0; i < 5; i ++)
            cout << a;
        for(int i = 0; i < 7; i ++)
            cout << b;
        for(int i = 0; i < 5; i ++)
            cout << c;
    }

    else cout << "none" << endl;
    return 0;
}

F

这题通过模拟举例子我们可以知道， 当n是奇数的时候，构造的数量就是（n+1)/2，当n是偶数的时候， 2和4构造不出， 其他均可构造， 但是最后一个数要比奇数的最后那个数+1

signed main()
{
    int n; cin >> n;
    if(n & 1)
    {
        int x = (n + 1)/2;
        cout << x << endl;
        for(int i = 1; i <= x; i ++)
            cout << i << " ";
        cout << endl;
    }
    else
    {
        if(n == 2 || n == 4) cout << "-1" << endl;
        else
        {
            int x = n / 2;
            cout << x << endl;
            for(int i = 1; i < x; i ++) cout << i << " ";
            cout << x + 1 << endl;
        }
    }
    return 0;
}

G

首先与运算，两个都是1才是1， 我们假设为行列，只有当该列的所有数字都是1的时候，不管中间经过多少次与运算，最后结果都是1， 但凡有一个0， 就不会成立，因为哪怕说中间的运算没有用过这个数的这个位子上的数， 最后的总计与运算也会将其变成0； 所以就是统计每列的1是否为n个即可， 其他都是幌子
本题需要加速

string s[1010];
int cnt[4010];
const int mod = 998244353;

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < n; i ++)
    {
        cin >> s[i];
        for(int j = 0; j < m; j ++)
            if(s[i][j] == '1')
               cnt[j] ++;
    }

    int q;cin >> q;
    while(q --)
    {
        int i, j, l, r, p;
        cin >> i >> j >> l >> r >> p;
    }

    int res = 0;
    for(int i = 0; i < m; i ++)
        if(cnt[i] == n) res ++;

    cout << res % mod << endl;
    return 0;
}

H

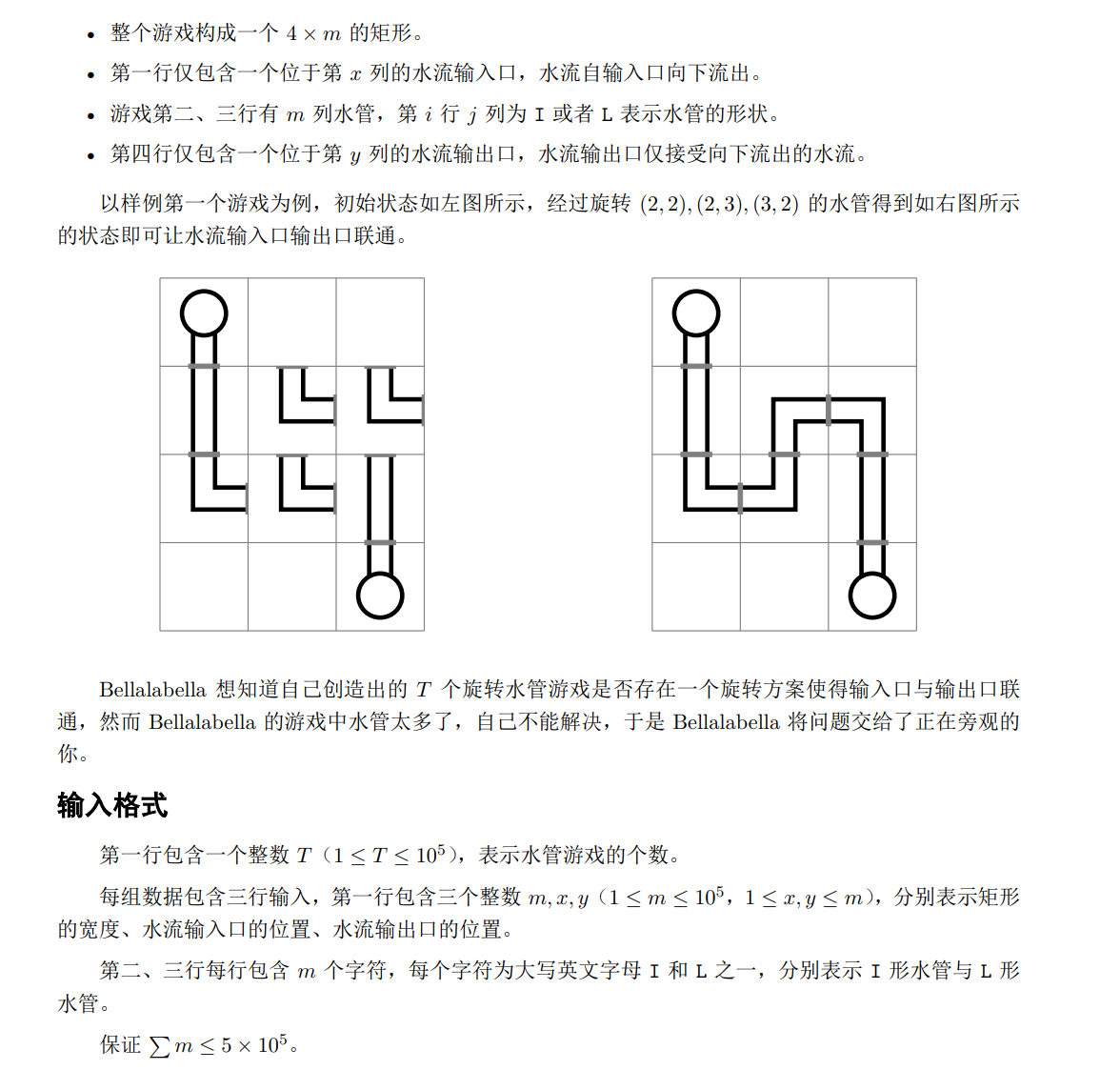
I: 只能从来的方向直行
L: 可以从来的方向左右走

int n, sx, sy;
const int N = 1e5 + 10;
bool st[5][N];
char g[5][N];

// 1下， 2上， 3左， 4右
int dfs(int x, int y, int d)
{
    if(x == 3 && y == sy) return true;

    if(st[x][y]) return false;
    if(x < 1 || x > 2 || y < 1 || y > n) return false;
    st[x][y] = 1;

    bool t;
    if(g[x][y] == 'I')
    {
        if(d == 1) t = dfs(x + 1, y, 1);
        else if(d == 2) t = dfs(x - 1, y, 2);
        else if(d == 3) t = dfs(x, y - 1, 3);
        else if(d == 4) t = dfs(x, y + 1, 4);
    }
    else
    {
        if(d == 1 || d == 2)
            t = (dfs(x, y + 1, 4) || dfs(x, y - 1, 3));
        else
            t = (dfs(x - 1, y, 2) || dfs(x + 1, y, 1));
    }

    st[x][y] = 0;
    return t;
}

void solved()
{
    cin >> n >> sx >> sy;
    for(int i = 1; i <= 2; i ++)
    {
        string s; cin >> s;
        for(int j = 1; j <= n; j ++)
        {
            st[i][j] = false;
            g[i][j] = s[j - 1];
        }
    }
    if(dfs(1, sx, 1)) cout << "YES" << endl;
    else cout << "NO" << endl;
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int t; cin >> t;
    while(t --) solved();
    return 0;
}

J

反证法
我们要找的是最大连通块， 且该连通块的mex = k (k = 0, 1, 2 ... n-1)， 当 k=0 时， 则找最大的不包括0的子树即可， 当k=1时， 我们找包含0但不包含1的最大子树， 其余同理

那么我们可以从0出发， 找当前权值为k的点，由当前点将整个树一分为二， 则一部分包含k（子树1）， 另一部分不包含k（子树2）；
我们此时只能得到关于子树1的全部信息，而该子树的mex也不可能是k，因为包含了k

siz[]存放的是子树1的节点数，mii存放着子树1的最小权值；

而子树2必须包含0~k-1, mex才会是k，如果说子树1中存在比k还要小的点， 那么，子树2就一定没有这个点， mex就一定不会是k了， 就不存在这样的子树；反之输出子树2的节点数 n - siz[j] 即可

由于本题将0作为根节点， 所以0需要特判， 直接输出最大子树即可

本题加速

const int N = 2e6 + 10;

int e[N], h[N], ne[N], idx;
int mii[N], pp[N], w[N], siz[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

//统计子树的节点个数
void dfs(int u, int fa)
{
    for(int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(j == fa) continue;

        dfs(j, u);
        siz[u] += siz[j];   //统计节点数
        mii[u] = min(mii[u], mii[j]);  //找子树的最小权值
    }
}

int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);

    memset(h, -1, sizeof h);
    memset(mii, 0x3f, sizeof mii);

    int n; cin >> n;

    for(int i = 1; i <= n; i ++) siz[i] = 1;

    int root = 0;
    for(int i = 1; i <= n; i ++)
    {
        cin >> w[i];
        if(w[i] == 0) root = i; // 在本题中， 我们将0当作根节点
        pp[w[i]] = i; // 记录值所对应的点
        mii[i] = w[i]; // 方便后期记录当前子树的最小权值
    }

    for(int i = 2; i <= n; i ++)
    {
        int x; cin >> x;
        add(x, i), add(i, x);
    }

    dfs(root, -1);

    for(int i = 0; i < n; i ++)
    {
        // 这种情况下，找最大连通块即可
        if(i == 0)
        {
            int mx = 0;
            for(int u = h[root]; ~u; u = ne[u]) // 不包含根节点
            {
                int j = e[u];
                mx = max(mx, siz[j]);
            }
            cout << mx << " ";
        }
        else
        {
            // 这种情况下， 其实就是将该树分为两块， 
            // 一块是包含k的连通块， 另一块是不包含k的连通块

            int j = pp[i]; //当前权值所对应的点

            // 如果说包含k的这部分 存在比 k 还小的点a，而这一部分已经包含了k，mex已不可能为k
            // 那么我们可以知道， 另一部分就没有该点a
            // 则另一部分的mex 就是该点a，所以不存在
            if(mii[j] < w[j])
                cout << "0" << " ";

            //如果不存在， 则另一部分包含了 0~k-1， 则mex为k，即为所求
            else cout << n - siz[j] <<" ";
        }
    }
    cout << n << endl;
    return 0;
}