排序算法详细总结

作者： 作者的头像   T-SHLoRk ,  2019-09-03 17:15:17 ,  所有人可见 ,  阅读 2678

54


82

本博客主要介绍了十种常见的内排序算法，TopK问题的常用五种解法，以及三数排序和结构体排序的介绍。

基本概念：

排序算法分类：

常见的内排序算法主要可以分为两类：

基于比较的排序：冒泡排序、选择排序、插入排序、快速排序、Shell排序、归并排序、堆积排序，其最坏情况下时间复杂度的不可能突破$O(nlogn)$。

非基于比较的排序：基数排序、计数排序、桶排序。

排序算法时间复杂度、稳定性比较

排序方法 平均时间复杂度 最坏时间复杂度 稳定性
冒泡排序 $O(n^2)$ $O(n^2 )$ 稳定
选择排序 $O( n^2 )$ $O( n^2 )$ 不稳定
插入排序 $O( n^2 )$ $O(n^2 )$ 稳定
快速排序 $O(n logn)$ $O( n^2 )$ 不稳定
Shell排序 $O( n^{1.23} )$ $O( n^2 )$ 不稳定
归并排序 $O(n logn)$ $O(n logn)$ 稳定
堆积排序 $O(n logn)$ $O(n logn)$ 不稳定

排序算法时间复杂度的简略证明

对于$n$个元素的序列，总共有$n!$中排列方式，只有一种是我们最终需要的结果（假设没有重复元素）。基于比较排序每进行一次比较后假设我们得到$A[i] < A[j]$，那么我们可以将$n!$中方案中所有$A[i] >A[j]$的排列都删除，最好的情况下，恰好$A[i] < A[j]$的排列组合方式和$A[i] > A[j]$的排列组合方式具有相同的数量，这样无论比较结果如何，我们都可以去除一半的排列组合方式。

总共有$n!$中方案，每次最多能够减去一半的方案，那么经过多少次比较能够使得只剩下一种方案呢？

由$2^k >= n!$，得到$k = log_2n! = log(n) + log(n-1) + … + log(2) + log(1) ～ O(nlogn)$。

不同排序算法

下述所有算法都以升序为例，数组下标范围为$A[0,n - 1]$。

冒泡排序算法:

冒泡排序算法每次交换相邻的两个数，如果左边的数小于右边的数，那么交换这两个元素，经过第一趟交换后，最大的元素肯定在最右边的位置上，然后对前$n - 1$个元素重复上述操作。

i指针控制每一趟交换的右边界，j指针控制每一趟交换中当前索引到的位置。

void BubbleSort(int n)
{
    for(int i = n - 1 ; i >= 0; i --)
    {
        for(int j = 0 ; j < i ; j ++)
        {       //  比较相邻元素，是否需要交换
            if(A[j] > A[j + 1])
                swap(A[j],A[j + 1]);
        }
    }
}

选择排序：

选择排序算法每次在未排序的数字中选择最大的那个数字放在数组末尾。

i指针控制当前未排序数字的右边界，也是当前未排序数字中最大的元素应该放的位置，我们使用idx代表当前最大元素的下标。每次在比较的时候我们只更新下标，避免频繁的数组元素交换。

void selectSort(int n)
{
    for(int i = n - 1; i >= 0 ; i --)
    {
        int idx = 0;
        for(int j = 0 ; j <= i ; j ++)
        {
            if(A[j] > A[idx])
                idx = j;
        }
        swap(A[i],A[idx]);
    }
}

选择排序.png

插入排序：

插入排序每次排序第k个元素，此时前k - 1个元素已经从小到大排好序了，我们从已经排序好的元素从后往前遍历，找到第一个小于当前元素的位置，那么当前元素就应该插在当前元素的后面。

void insertSort(int n)
{
    for(int i = 0 ; i < n ; i ++)
    {
        for(int j = i - 1 ; j >= 0 && A[j] > A[j + 1] ; j -= 1)
            swap(A[j],A[j + 1]);
    }
}

插入排序.png

快速排序：

快速排序使用了分治的思想，首先假设我们当前排序的区间为$A[L:R]$，我们首先在这个区间内部选择一个数字作为基准$pivot$。然后我们将所有小于$pivot$的元素都放在该基准元素的左边，将所有大于$pivot$的元素都放在该基准元素的右边。为了实现上述效果：我们从右往左找到第一个小于基准元素的元素，从左往右找到第一个大于基准元素的元素，交换这两个元素。

这里需要特别注意的是：

如果我们选择的基准元素是区间最左边的元素，那么我们要先从右往左找。

如果我们选择的基准元素是区间最右边的元素，那么我们要先从左往右找。

这时候基准元素肯定在正确的位置上，接下来我们递归的对左右两个区间进行排序。

//  当前排序区间为[l,r]
//  我们选择的基准元素是区间最左边元素，这时候while循环内部先从右往左找
//  结束while循环后，我们将基准元素交换到对应的位置上。
void quickSort(int l,int r)
{
    if(l >= r) return;
    int pivot = A[l];
    int i = l,j = r;
    while(i < j)
    {
        while(i < j && A[j] >= pivot) j --;
        while(i < j && A[i] <= pivot) i ++;
        if(i < j)
            swap(A[i],A[j]);
    }
    swap(A[l],A[i]);
    quickSort(l,i - 1);
    quickSort(i + 1,r);
}

快速排序.png

归并排序

归并排序首先将区间$[l,r]$分为两个左右两个子区间，然后先将两个子区间内部排好序，然后我们使用双指针的算法，将两个子区间合并。

void mergeSort(int l,int r)
{
    if(l == r) return;
    int mid = (l + r) >> 1;
    mergeSort(l,mid);
    mergeSort(mid + 1,r);
    int temp[r - l + 1],k = 0,i,j;
    for(i = l,j = mid + 1;i <= mid && j <= r;k ++)
    {
        if(A[i] < A[j]) temp[k] = A[i ++];
        else temp[k] = A[j ++];
    }
    while(i <= mid) temp[k ++] = A[i ++];
    while(j <= r) temp[k ++] = A[j ++];
    for(int i = l,k = 0;i <= r ; i ++,k ++)
        A[i] = temp[k];
}

归并排序.png

Shell排序：

Shell排序也称为缩小增量排序。我们首先将所有距离为gap的元素划分为一组，先将每一组内部使用某种算法排好序（这里我们使用插入排序）。

如我们将A[0],A[gap],A[2*gap],...,A[k*gap]划分为一组，A[1],A[gap + 1],A[2*gap + 1],...,A[k*gap + 1]划分为一组。然后我们不断的缩小gap，直至gap = 1时，我们就将整个数组排好序了。

常用情况是初始gap = n / 2，每次将gap变为原来的一半。

//  这里需要注意的是，思想上分组排序，实际上是每一组交替进行。
//  第一层循环，更新gap
//  第二层循环，迭代当前需要将哪一个数字按照选择排序的方式在组内排好序
//  第三层循环，A[j]在当前组内（`A[j],A[j - gap],A[j - 2*gap],...,A[j - k*gap]`）进行插入排序
void shellSort(int n)
{
    for(int gap = n / 2; gap > 0 ; gap = gap / 2)
    {
        for(int i = gap ; i < n ; i ++)
        {
            for(int j = i - gap ; j >= 0 && A[j] > A[j + gap] ; j -= gap)
                swap(A[j],A[j + gap]);
        }
    }
}

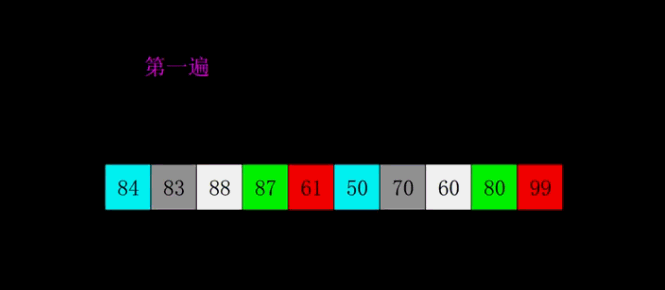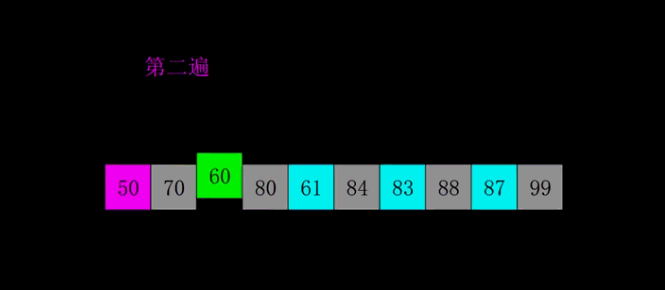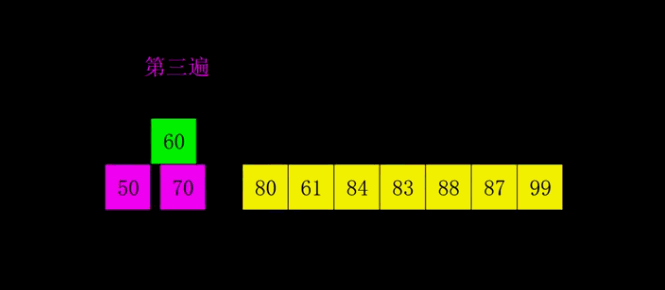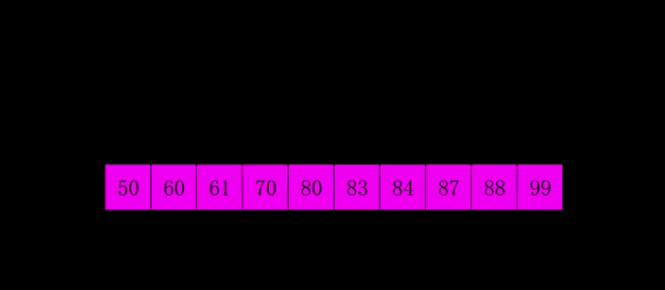
Shell排序.png

堆积排序：

堆积排序的思想是首先将$n$个元素建立成一个大顶堆，然后从大顶堆弹出当前堆顶元素也就是最大的元素，然后将剩余$n-1$个元素重新更新大顶堆得到次大的元素，直至得到所有的元素。

堆积排序主要分为两个重要的过程，建立大顶堆和更新大顶堆。这里我们使用数组A[0:n-1]来模拟大顶堆，根节点序号为idx，那么其左右孩子的序号分别为2 * idx和2 * idx + 1。

更新大顶堆：假设我们已经得到了初始的大顶堆，我们将大顶堆堆顶元素A[0]和A[n - 1]交换，交换后，我们发现除了根节点，左右两颗子树还是大顶堆的。这时候我们只需要将大顶堆堆顶的元素和两个孩子中较大的那个孩子交换，直至交换到叶节点。

初始建堆：假设堆有d层，那么我们将d - 1层最右边的结点开始，从右到左，从下到上更新以当前节点为根节点的大顶堆进行更新。进行更新完后，我们就可以得到一个大顶堆了。

堆积排序.png 

//  记录根节点的值，`root`是根节点索引，`j`是左孩子节点索引，`n`代表当前堆内的有效元素个数
//  如果当前根节点有右孩子，并且右孩子大于左孩子，更新`j`为左右孩子较大值的那个节点索引
//  如果当前根节点大于较大的孩子节点，那么就不用交换了
//  否则将当前根节点的值变为较大孩子节点的值，同时更新当前根节点为较大孩子节点
void adjust(int root,int n)
{
    int temp = A[root],j = 2 * root + 1;
    while(j < n)
    {
        if(j + 1 < n && A[j] < A[j + 1])
            j ++;
        if(temp >= A[j])
            break;
        A[(j - 1) / 2] = A[j];
        j = 2 * j + 1;
    }
    A[(j - 1) / 2] = temp;
}
//  首先将前`n - 1`个节点为根节点的子树进行调整，建立一个大顶堆
//  将堆顶元素弹出，并更新大顶堆
void heapSort(int n)
{
    for(int i = n / 2;i >= 0 ; i --)
        adjust(i,n);
    for(int i = n - 1 ; i >= 0 ; i --)
    {
        swap(A[0],A[i]);
        adjust(0,i);
    }
}

计数排序：

使用哈希表统计每个元素出现的个数，然后按照键值从小到大把每个元素输出其出现的次数。计数排序适用于数据范围不大的时候进行排序。

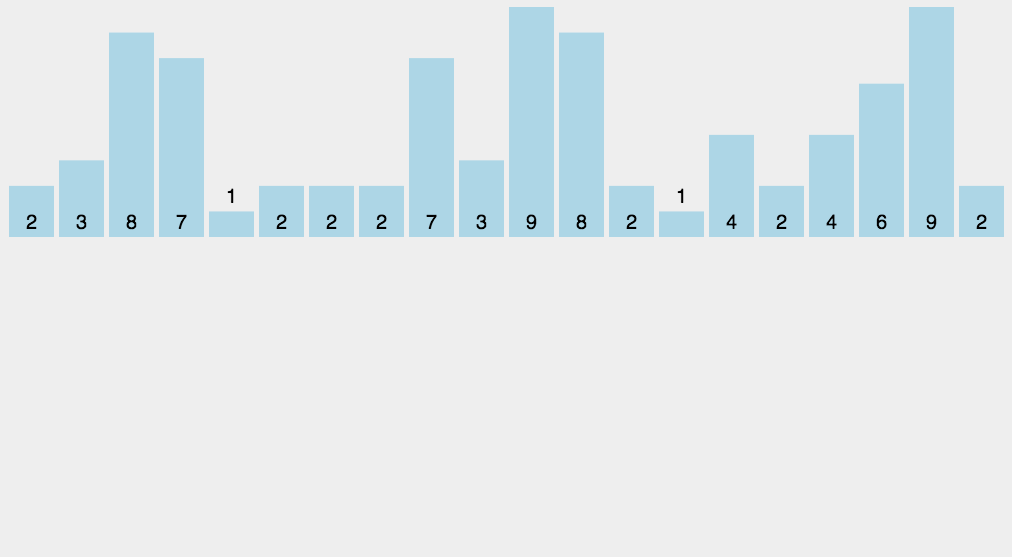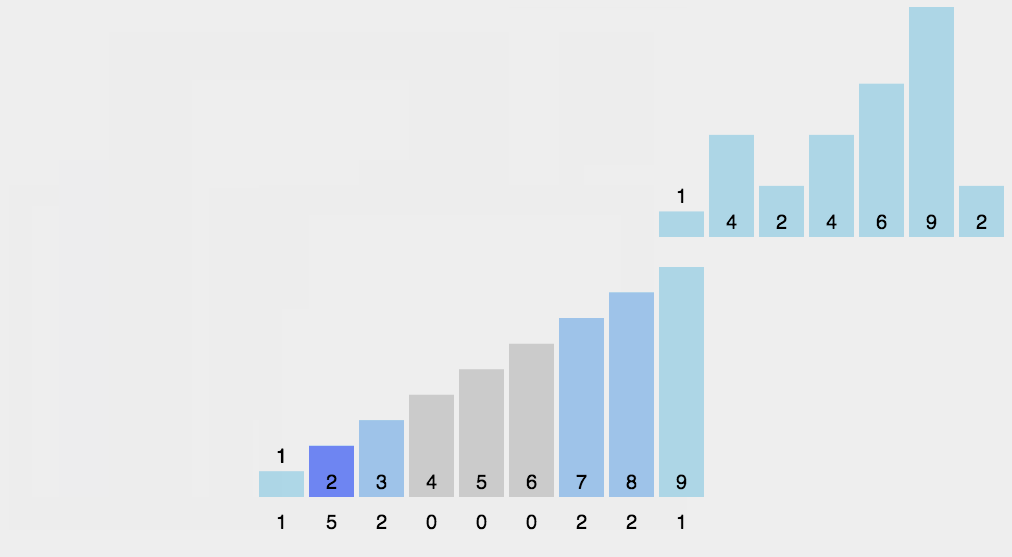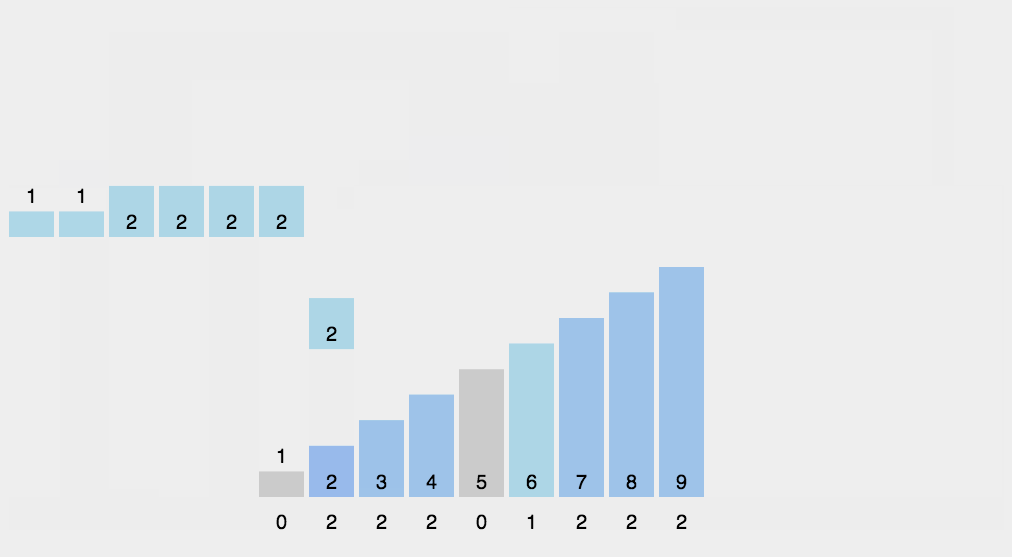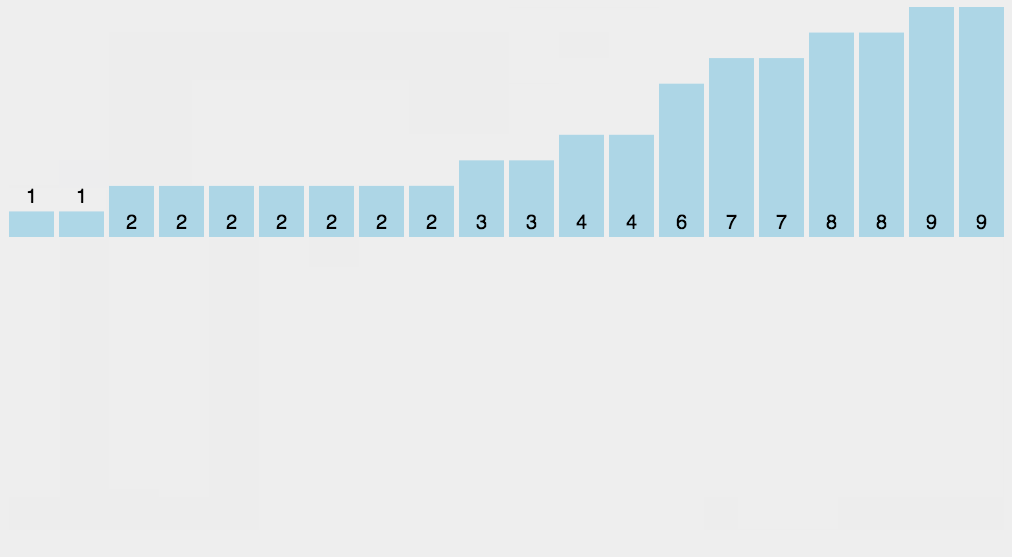
计数排序.png

桶排序

桶排序 (Bucket sort)原理是将数组分到有限数量的桶子里，然后对每个桶子再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序），最后将各个桶中的数据有序的合并起来。

假设我们的映射函数$f(x_1) = k_1,f(x_2)=k_2$，如果桶的序号$k_1<k_2$，那么必然有$x_1<x_2$。所以我们只需要将桶内元素排好序，再将若干个桶元素拼接起来即可。假设总共$N$个元素$M$个桶，那么最好情况下每个桶有$N/M$个元素，如果桶内采用基于比较的排序算法，那么总的时间复杂度就是$O(M*(N/M)log(N/M))=O(Nlog(N/M))$。

所以桶排序适用于

排序过程：

  1. 假设待排序的一组数统一的分布在一个范围中，并将这一范围划分成几个子范围，也就是桶
  2. 将待排序的一组数，分档规入这些子桶，并将桶中的数据进行排序
  3. 将各个桶中的数据有序的合并起来

基数排序

基数排序是将待排序的元素拆分为$k$个关键字（比较两个元素时，先比较第一关键字，如果相同再比较第二关键字……），然后先对第$k$关键字进行稳定排序，再对第$k-1$关键字进行稳定排序，再对第$k-2$关键字进行稳定排序……最后对第一关键字进行稳定排序，这样就完成了对整个待排序序列的稳定排序。

Acwing 785排序题解

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010;

int A[N];
void quickSort(int l,int r)
{
    if(l >= r) return;
    int pivot = A[l];
    int i = l,j = r;
    while(i < j)
    {
        while(i < j && A[j] >= pivot) j --;
        while(i < j && A[i] <= pivot) i ++;
        if(i < j)
            swap(A[i],A[j]);
    }
    swap(A[l],A[i]);
    quickSort(l,i - 1);
    quickSort(i + 1,r);
}
void selectSort(int n)
{
    for(int i = n - 1; i >= 0 ; i --)
    {
        int idx = 0;
        for(int j = 0 ; j <= i ; j ++)
        {
            if(A[j] > A[idx])
                idx = j;
        }
        swap(A[i],A[idx]);
    }
}
void BubbleSort(int n)
{
    for(int i = n - 1 ; i >= 0; i --)
    {
        for(int j = 0 ; j < i ; j ++)
        {
            if(A[j] > A[j + 1])
                swap(A[j],A[j + 1]);
        }
    }
}
void insertSort(int n)
{
    for(int i = 0 ; i < n ; i ++)
    {
        int j = i - 1,temp = A[i];
        while(j >= 0 && A[j] > temp)
        {
            A[j + 1] = A[j];
            j --;
        }
        A[j + 1] = temp;
    }
}
void insertSortV2(int n)
{
    for(int i = 0 ; i < n ; i ++)
    {
        for(int j = i - 1 ; j >= 0 && A[j] > A[j + 1] ; j -= 1)
            swap(A[j],A[j + 1]);
    }
}
void quickInsertSort(int n)
{
    for(int i = 0 ; i < n ; i ++)
    {
        int l = 0,r = i - 1,temp = A[i];
        while(l < r)
        {
            int mid = (l + r) >> 1;
            if(A[mid] > temp) r = mid;
            else l = mid + 1;
        }
        if(A[l] < temp)
            continue;
        for(int j = i - 1 ; j >= l ; j --)
            A[j + 1] = A[j];
        A[l] = temp;
    }
}
void mergeSort(int l,int r)
{
    if(l == r) return;
    int mid = (l + r) >> 1;
    mergeSort(l,mid);
    mergeSort(mid + 1,r);
    int temp[r - l + 1],k = 0,i,j;
    for(i = l,j = mid + 1;i <= mid && j <= r;k ++)
    {
        if(A[i] < A[j]) temp[k] = A[i ++];
        else temp[k] = A[j ++];
    }
    while(i <= mid) temp[k ++] = A[i ++];
    while(j <= r) temp[k ++] = A[j ++];
    for(int i = l,k = 0;i <= r ; i ++,k ++)
        A[i] = temp[k];
}
void shellSort(int n)
{
    for(int gap = n / 2; gap > 0 ; gap = gap / 2)
    {
        for(int i = gap ; i < n ; i ++)
        {
            for(int j = i - gap ; j >= 0 && A[j] > A[j + gap] ; j -= gap)
                swap(A[j],A[j + gap]);
        }
    }
}
void adjust(int root,int n)
{
    int temp = A[root],j = 2 * root + 1;
    while(j < n)
    {
        if(j + 1 < n && A[j] < A[j + 1])
            j ++;
        if(temp >= A[j])
            break;
        A[(j - 1) / 2] = A[j];
        j = 2 * j + 1;
    }
    A[(j - 1) / 2] = temp;
}
void heapSort(int n)
{
    for(int i = n / 2;i >= 0 ; i --)
        adjust(i,n);
    for(int i = n - 1 ; i >= 0 ; i --)
    {
        swap(A[0],A[i]);
        adjust(0,i);
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 0; i < n ; i ++)
        scanf("%d",&A[i]);
    //quickSort(0,n - 1);
    //BubbleSort(n);
    //insertSort(n);
    //insertSortV2(n);
    //quickInsertSort(n);
    //selectSort(n);
    //mergeSort(0,n - 1);
    //shellSort(n);
    heapSort(n);
    for(int i = 0 ; i < n ; i ++)
        printf("%d ",A[i]);
    return 0;
}

其他常见排序相关问题

求数组中第$k$小/大的元素。

解法一：排序算法

当数组长度为$n$，并且数组长度不是很大的时候，我们可以对其进行排序，然后取第$k$个元素，总的时间复杂度为$O(nlogn )$。

但是其实我们只需要找到第$k$个元素，并不关心前面的元素和后面的元素是否已经排好序了，所以我们可以只对前$k$个元素进行排序，我们可以使用冒泡排序，选择排序、插入排序等排好前$k$个数，总的时间复杂度为$O(n*k)$ 。

解法二：分治

我们考虑一下我们在进行快速排序的时候，我们选择一个基准元素个pivot，将小于基准元素的数字都放在左边，大于基准元素的数字都放在右边。如果左边元素的个数大于等于$k$，那么继续左半区间找到第$k$的数；如果左边元素个数恰好等于$k-1$，那么基准元素就是第$k$小的数；否则，假设左半区间有$x$个数，那么我们只需要在有半区间找到第$k-x-1$小的数就可以了。平均的时间复杂度是$nlogk$的。

同样的c++内置函数nth_element函数也是以类似于该思想实现的，期望时间复杂度为$O(n)$。

    //  求第`k`小的元素，这里`k`从1开始
    //  nth_element(start,start + n,end)可以让第`n`小的元素放在nums[n]的位置上，这是`n`从0开始
    int getKthValue(vector<int>& nums,int l,int r,int k)
    {
        if(l == r) return nums[l];
        int i = l,j = r,pivot = nums[l];   
        while(i < j)
        {
            while(i < j && nums[j] >= pivot) j --;
            while(i < j && nums[i] <= pivot) i ++;
            if(i < j) 
                swap(nums[i],nums[j]);
        }
        swap(nums[l],nums[i]);
        if(i - l >= k) return getKthValue(nums,l,i - 1,k);
        else if(i - l + 1 == k) return nums[i];
        else return getKthValue(nums,i + 1,r,k - (i - l + 1));
    }

解法三：二分

假设数组中元素的最小值和最大值分别是$V_{min},V_{max}$，那么我们期望找到的结果肯定就在这个区间内。我们可以在$O( n )$的时间复杂度内求出数组中比pivot大的元素有多少个。那么我们可以利用二分查找的思想找到一个数字$p$，它是大于等于$p$的元素个数大于$k$的最小值。时间复杂度$O(nlog(V_{max}-V_{min}))$

解法四：堆积排序

这个思路很容易理解（以求第$k$大的数为例），我们维护一个大小为$k$的小顶堆，如果新元素比堆顶元素大的话，那么弹出堆顶元素，并将新元素插入堆，这样可以保证堆内始终维护的是最大的$k$个数，那么堆顶元素自然也就是第$k$大的数。具体代码见下面题解。这里我们模拟了一个堆，其实可以用c++优先队列priority_queue来解决。时间复杂度$O(nlogk)$

解法五：计数排序

如果数字的范围并不是很大，我们使用一个数组存储每个数字出现的个数，然后从小往大雷加每个数字出现的次数，等到第一次累加次数大于$k$，当前数字就是第$k$小的元素了，具体代码见下面题解。时间复杂度$O(n)$。

Acwing786题解：求第K小的数

分治：

#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
const static int N = 100010;
int A[N];
int getKthSmallest(int l,int r,int k)
{
    if(l == r) return A[l];
    int i = l,j = r,pivot = A[l];
    while(i < j)
    {
        while(i < j && A[j] >= pivot) j --;
        while(i < j && A[i] <= pivot) i ++;
        if(i < j) swap(A[i],A[j]);
    }
    swap(A[l],A[i]);
    if(i - l >= k) return getKthSmallest(l,i - 1,k);
    else if(i - l + 1 == k) return pivot;
    else return getKthSmallest(i + 1,r,k - (i - l + 1));
}
int main()
{
    int n,k;
    scanf("%d %d",&n,&k);
    for(int i = 0 ; i < n ; i ++)
        scanf("%d",&A[i]);
    printf("%d",getKthSmallest(0,n - 1,k));
    return 0;
}

堆积排序

#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
const static int N = 100010;
int heap[N];
void adjust(int root,int k)
{
    int temp = heap[root],j = 2 * root + 1;
    while(j < k)
    {
        if(j + 1 < k && heap[j] < heap[j + 1])
            j ++;
        if(temp > heap[j])
            break;
        heap[(j - 1) / 2] = heap[j];
        j = 2 * j + 1;
    }
    heap[(j - 1) / 2] = temp;
}
int main()
{
    int n,k,cur;
    scanf("%d %d",&n,&k);
    for(int i = 0; i < n ; i ++)
    {
        scanf("%d",&cur);
        if(i < k) 
        {
            heap[i] = cur;
            if(i == k - 1)
            {
                for(int j = k / 2 ; j >= 0 ; j --)
                    adjust(j,k);
            }
        }else if(cur < heap[0])
            {
                heap[0] = cur;
                adjust(0,k);
            }
    }
    printf("%d",heap[0]);
    return 0;
}

计数

//  这里数据范围比较大，所以我用的hash表，但是这样插入操作会带来额外的时间复杂度。
//  如果数据范围比较小，直接用数组模拟，时间复杂度为O(n)
#include<cstring>
#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
const static int N = 100010;
map<int,int> cnt_map;
int main()
{
    int n,k,cur,cnt = 0;
    scanf("%d %d",&n,&k);
    for(int i = 0 ; i < n ; i ++)
    {
        scanf("%d",&cur);
        cnt_map[cur] ++;
    }
    for(auto &it : cnt_map)
    {
        cnt += (int)it.second;
        if(cnt >= k)
        {
            printf("%d",(int)it.first);
            break;
        }
    }
    return 0;
}

三数排序

三数排序指的是给一个无序的数组，将所有小于当前元素的数字都放在该数字的前面，所有大于当前元素的数字都放在该数字的后面。这里以Leetcode75题为例。

75. Sort Colors

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example:

Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

Follow up:

  • A rather straight forward solution is a two-pass algorithm using counting sort.
    First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.
  • Could you come up with a one-pass algorithm using only constant space?

题意：给一个只包含0，1的数组，请用常数空间并且只扫描数组一遍将所有的0，1，2 分别放在一起。

题解：和很多的双指针题目一样，我们设立指针代表当前位置之前的数字已经排好了。对于这一题，我们设立i指针代表当前位置之前的元素都是0，设立j指针代表当前位置之后的元素都是2。我们再使用一个k来表示遍历数组。当nums[k] = 0时，我们将当前位置的元素和nums[i]交换，并且k ++，这是因为交换过来的数字必定是1，如果是2的话肯定在更早的位置被交换到最后面了。

当nums[k] = 2时，我们将当前位置的元素和nums[j]交换，此时不能k ++，因为我们并不知道当前交换过来的数字到底是几，必须重新判断。

当nums[k] = 1时，我们直接k ++，不交换。

    void sortColors(vector<int>& nums) {
        int n = nums.size();
        for(int i = 0, j = n - 1,k = 0;k <= j ;)
        {
            if(nums[k] == 0) swap(nums[i ++],nums[k ++]);
            else if(nums[k] == 2) swap(nums[j --],nums[k]);
            else k ++;
        }
    }

自定义排序

在做题目的过程中，我们经常需要对结构体进行排序，或者自定义一种比较顺序。对于结构体来说我们通常只需要重载其<运算符就可以了。这一部分的详细讲解可以看 结构体排序 。

参考文献

十大经典排序算法：https://www.cnblogs.com/onepixel/p/7674659.html

快速排序为什么那么快：http://mindhacks.cn/2008/06/13/why-is-quicksort-so-quick/

编程之美2.5节：寻找最大的K个数

13 评论

用户头像
Blade   2020-03-03 21:16         踩      回复

Acwing 785排序题解, ac不了，写的有问题

用户头像
T-SHLoRk   2020-03-05 12:33         踩      回复

是因为785题数据量只支持$O(nlogn)$复杂度的排序算法。

用户头像
Blade   2020-03-05 18:34    回复了 T-SHLoRk 的评论         踩      回复

你的快排过不了，我是学快排的时候看的你写的，你只取最左边的作为基准，然后就慢了，建议改成中间作为基准或随机选一个作为基准。

用户头像
T-SHLoRk   2020-03-07 12:38    回复了 Blade 的评论         踩      回复

嗯嗯，刚才试了一下，应该是数据增强了。可能会有数据卡到这个基准。

用户头像
肖畅   2020-02-28 21:40         踩      回复

大佬 太厉害了 写得很好 赞一个

用户头像
Diamondz   2019-11-10 14:50         踩      回复

总结的很好，赞一个👍

用户头像
Anlans   2019-09-03 19:20         踩      回复

### 干货，加油

用户头像
T-SHLoRk   2019-09-03 20:01         踩      回复

谢谢支持

用户头像
yxc   2019-09-03 18:33         踩      回复

这个总结很到位！赞一个！

用户头像
T-SHLoRk   2019-09-03 20:04         踩      回复

谢谢 鼓励。现在Acwing支持目录嘛？我添加[TOC]后好像没有识别

用户头像
yxc   2019-09-03 23:29    回复了 T-SHLoRk 的评论         踩      回复

目录功能会尽快支持~

用户头像
jasonlin   2020-06-04 08:59         踩      回复

如果 收藏别人分享的时候 如果能加tag的话 ， 找起来会方便很多鸭

用户头像
yxc   2020-06-09 10:13    回复了 jasonlin 的评论         踩      回复

收到