二分图的定义

可以把图里所有的点划分到两边，分成两个集合使得集合内没有边，也就是说同一个集合中任意两点间不能有边。这样的图就叫做二分图。

二分图的判定

这个图是二分图当且仅当图内没有奇数环（点数为奇数的环）。

证明：

反证法：如果图内有奇数环，那么把里面任意一点归入一号集合中，他右面的就得归入二号集合中，再右边的又是一号集合，这么一直归入下去，发现最初的那一点又要归入二号集合中，这就矛盾了，所以不行。

如果图里没有奇环，那么这张图是否一定是二分图呢？答案是正确的。
把一个点归到左边，再把所有与他相邻的点归到右边，再把所有与他们相邻的点归到左边，由于没有负环，所以肯定能弄完。
这个过程可以叫做染色

染色法判定二分图：

可以用深度优先搜索的方法。
遍历一遍所有的点，如果 $i$ 未染色，就给 $i$ 染色(dfs)。

代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int n, m;
int h[N], e[2 * N], ne[2 * N], idx;
int color[N];

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
bool dfs(int u, int c){
    color[u] = c;
    for (int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        if (!color[j])
            if (!dfs(j, 3 - c)) return false;
        else if (color[j] == c) return false;
    }
    return true;
}
int main(){
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m--){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    bool flag = true;
    for (int i = 1; i <= n; i ++ ){
        if (!color[i]){
            if (!dfs(i, 1)){
                flag = false;
                break;
            }
        }
    }
    if (flag) puts("Yes");
    else puts("No");
    return 0;
}

匈牙利算法：

他主要是解决这个问题的，又称月老算法，找女友算法，这都什么话你说说。

他的主要思路要用图表示：
假设有这样一张二分图

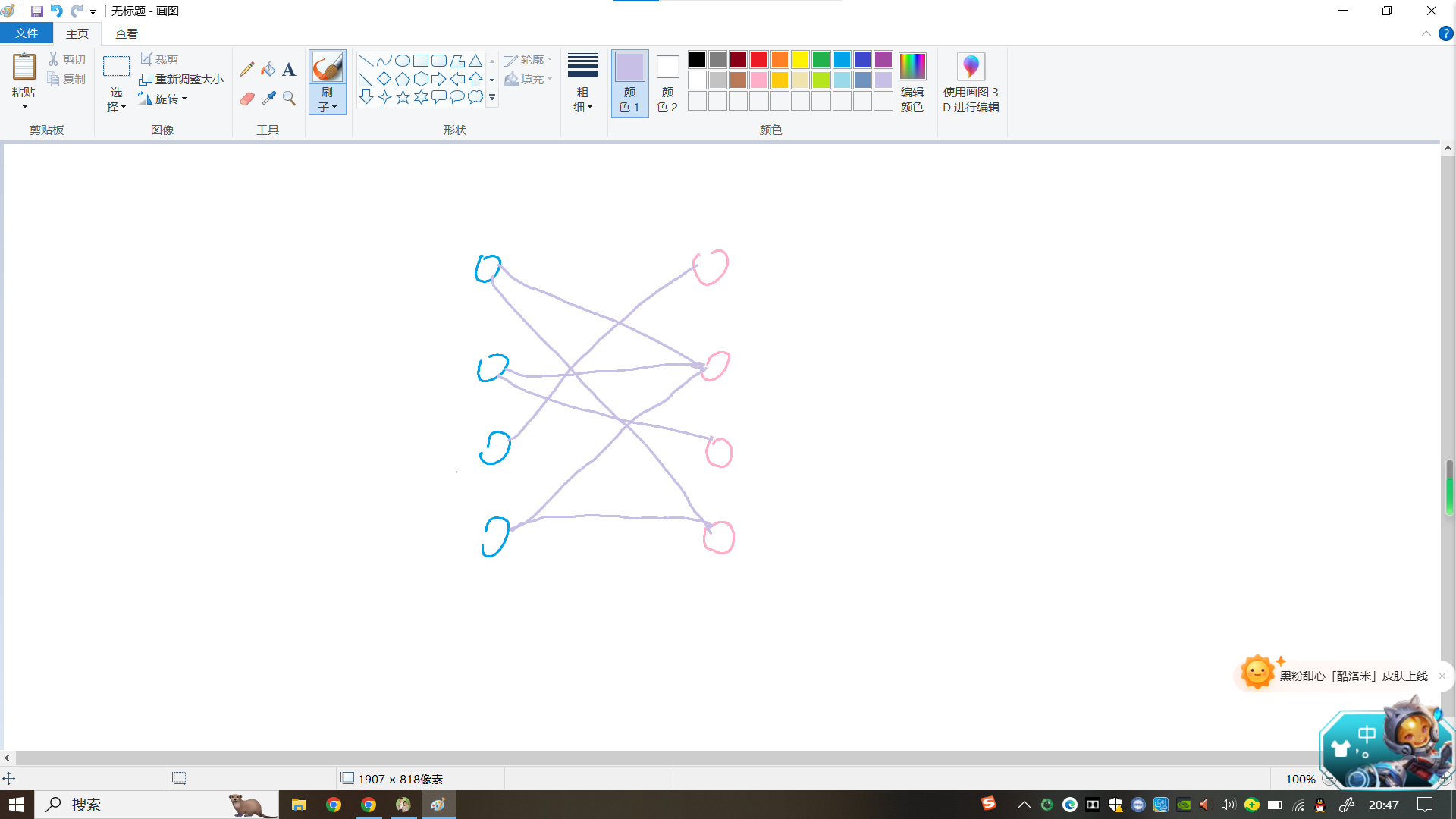
知道为什么要用这种配色吗？
我们可以把左边看成男生，右边看成妹子，然后把线看成有一定好感度。
这样，题就变成了确定尽量多的正当的恋爱关系，即不能脚踏多条船。突然感觉算法好玩多了……
要是男生或女生之间互相连边就不符合二分图的定义了吗，咳，当然法律也不允许……

我们可以先给一号男生确定恋爱关系，他第一个喜欢的是二号女生，而且二号还是单身状态，可以确定第一对恋爱关系。二号是女神吗，这么多人喜欢，喜欢上她真是个正确的选择吗？

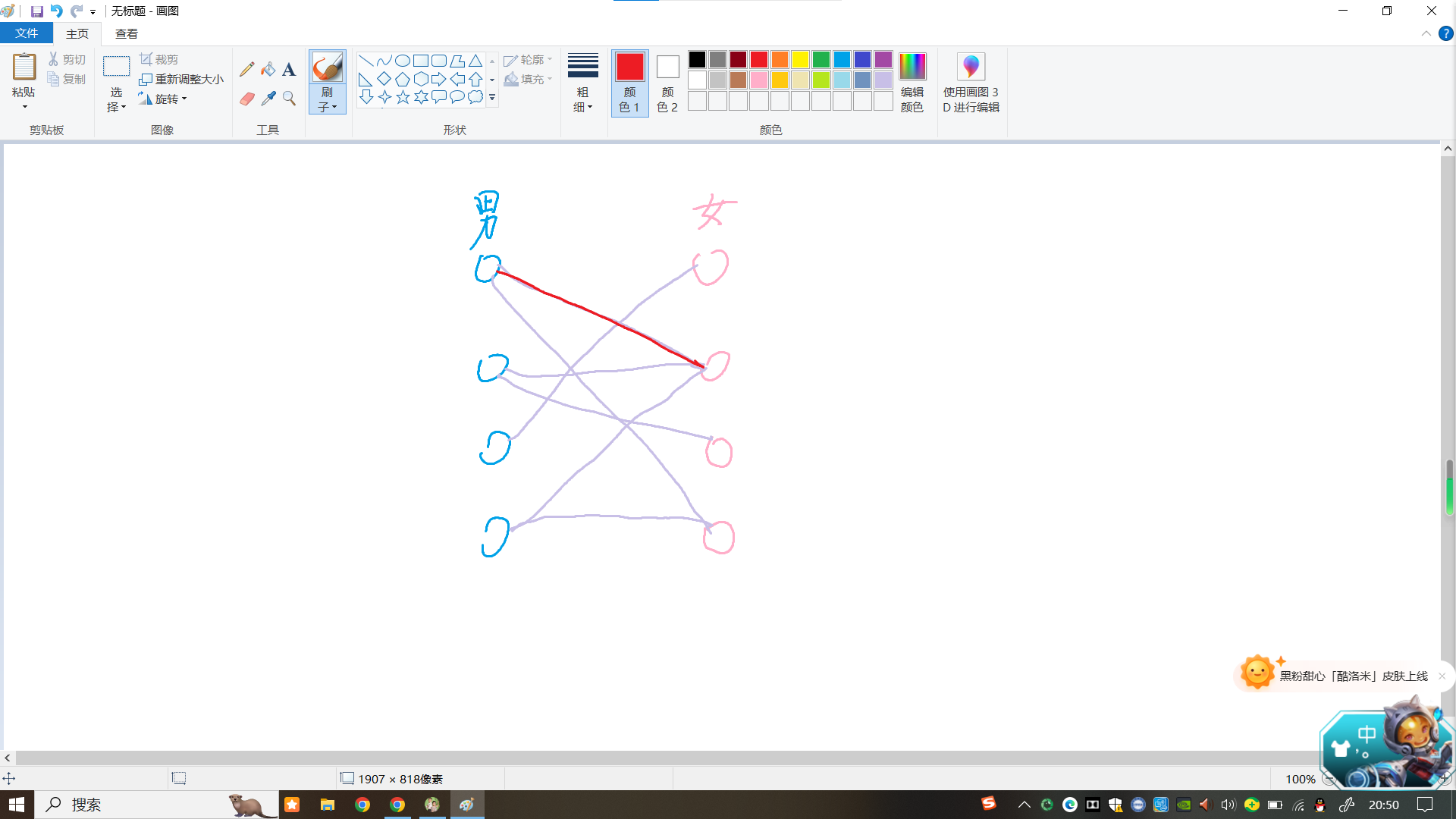
月老吗，当然要用红线。

轮到第二个男生选的时候，发现竟然还想选 $2$ 号女生，于是他就去劝劝 $1$ 号男生看能不能选别人，发现正好能选别人，于是他就去勾搭那个了，而 $2$ 号男生就选了 $2$ 号女生可以用一个比较真实的颜色来拒绝掉。在看人家 $3$ 号男生，一见钟情好吧，恭喜他喜结良缘（多学学人家）。

最后，$2$ 号女生真的是女神啊，又被 $4$ 号男生看上了，跟 $2$ 好沟通之后。他们都有了完美的结局。

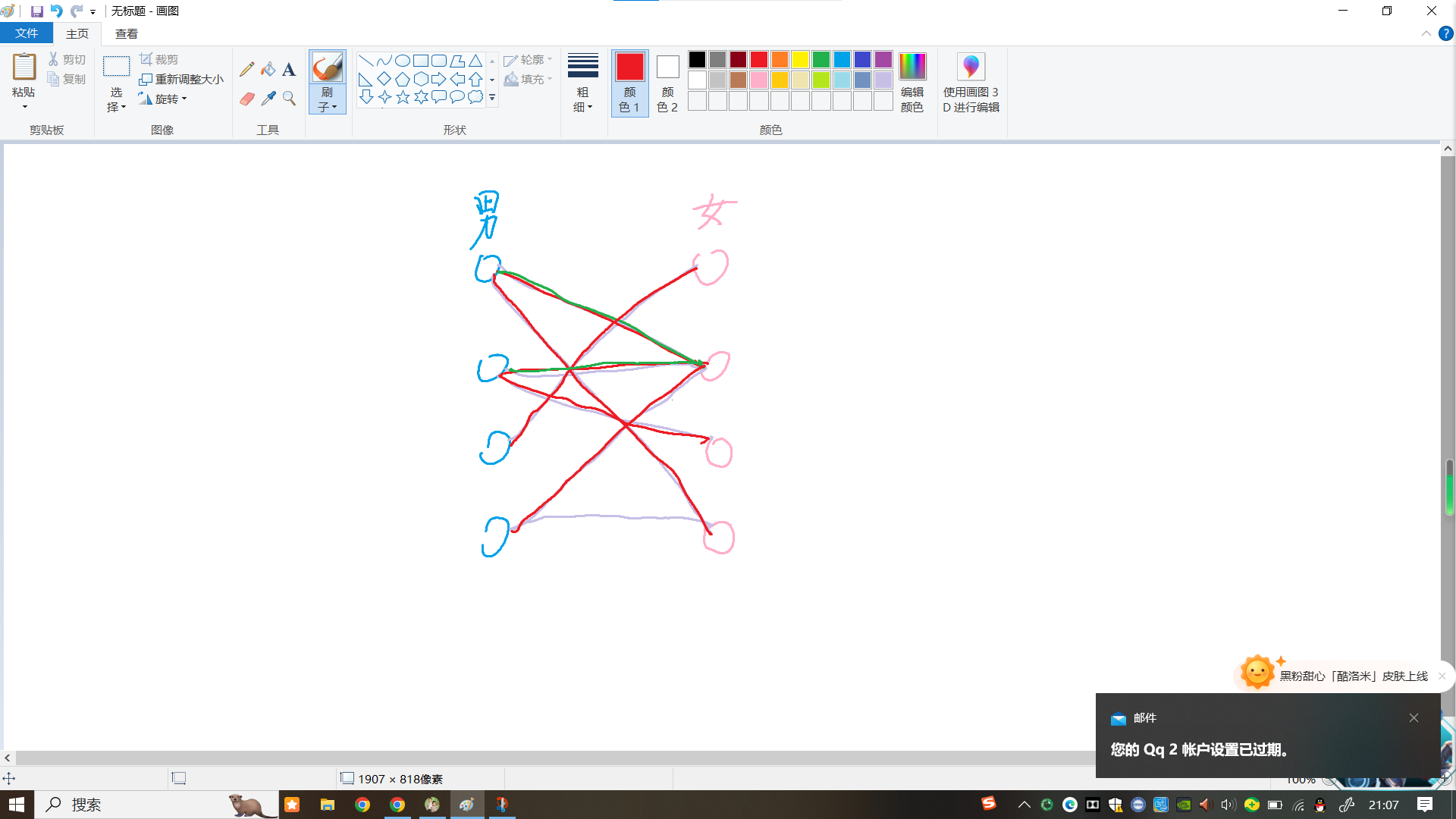
额……整个算法思路就是这样的，除非男人没有其他选择，不然其他人来抢亲肯定是会答应的。

代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
bool find(int x){
    for (int i = h[x]; i != -1; i = ne[i]){
        int j = e[i];
        if (!st[j]){
            st[j] = true;
            if (match[j] == 0 || find(match[j])){
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}
int main(){
    scanf("%d%d%d", &n1, &n2, &m);
    memset(h, -1, sizeof h);
    while (m--){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    int res = 0;
    for (int i = 1; i <= n1; i++){
        memset(st, false, sizeof st);
        if (find(i)) res++;
    }
    printf("%d\n", res);
    return 0;
}