传送门
$\quad$将原问题转化成一个组合数问题，枚举不为$0$的数字的个数。每一个被枚举的方案之间，由于不为$0$的数字个数是不一样的，所以方案肯定是不同的。
$\quad$枚举完不为$0$的数字以后，我们需要考虑这样一个问题。假设当前不为$0$的数字和为$N$，因此考虑的问题就是，将$N$，表示成若干个数的和有几种表示的方法。

$\quad$这个问题就是组合数学的隔板问题，假设现在不为$0$的数字个数为$i$，将$N$表示成$i$个数的表示方法，每一种表示方法，即对应我们一种数字的排列。

这个证明过程如下：

$\quad$上面的证明过程有些不严谨，事实上当和为$N$时，棒的放置位置应该是有$N - 1$个。

$\quad$有了这个前置的知识以后，对于枚举的不为$0$的数为$i$的情况下，其能组合的排列方式即为：$$C(i - 1 , i - 1) + C( i , i - 1) + C( i + 1, i - 1 ) + … C(n - 1, i - 1) = C(n , i)$$

$\quad$这条式子，就是常用的组合数的公式(证明过程暂时略)

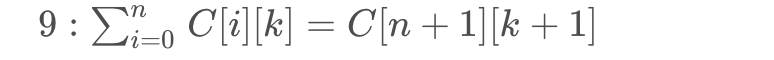
Code

#include<bits/stdc++.h>
#pragma optimize(2)
#define endl '\n'
#define ll() to_ullong() 
#define string() to_string()
#define Endl endl
using namespace std;
typedef long long ll;
typedef pair<int,int>PII; 
typedef unsigned long long ull;
const int M=2010;
const int P=13331;
const ll  llinf=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
const int mod=1e6+3;
const int N=1e6+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
int fact[N] , infact[N];
int qmi(int a , int b )
{
  int res = 1;
  while(b)
  {
    if(b&1)res = 1ll * res * a %mod;
    a = (1ll * a * a)%mod;
    b >>= 1;
  }
  return res;
}
void init()
{
  fact[0] = infact[0] = 1;
  for(int i = 1 ; i <= 500000 ; i ++)
  {
    fact[i] = (1ll * fact[i - 1] * i ) % mod;
    infact[i] = 1ll * infact[i - 1] * qmi( i , mod - 2) % mod;
  }
}
//c( n , m ) = n!/[( n - m)! * m !]
int c(int a, int b )
{
  return 1ll * fact[a] * infact[a - b] % mod * infact[b] % mod;
}
int sum[N];
// n = 5 m = 1
// 
void solve()
{
   int m , n;
   cin>>n>>m;
   init();
   int ans = 0;

   for(int i = 1 ; i <= min( m , n) ; i ++)//枚举 选了 几个 位置
   {
     //c (n - 1 , i - 1)
     ans = (ans + 1ll * c(m , i ) * c( n  , i ) % mod)%mod;
     //c(j , i - 1)   j = [i - 1 , n - 1]
     //c(i - 1 , i - 1) + c(i , i - 1) + c( i + 2 , i - 1) + ... + c(n - 1 , i - 1) = c(n , i )
   }
   cout<<ans<<endl;
   return ;
}
signed main()
{
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
        solve();
        return 0;
}