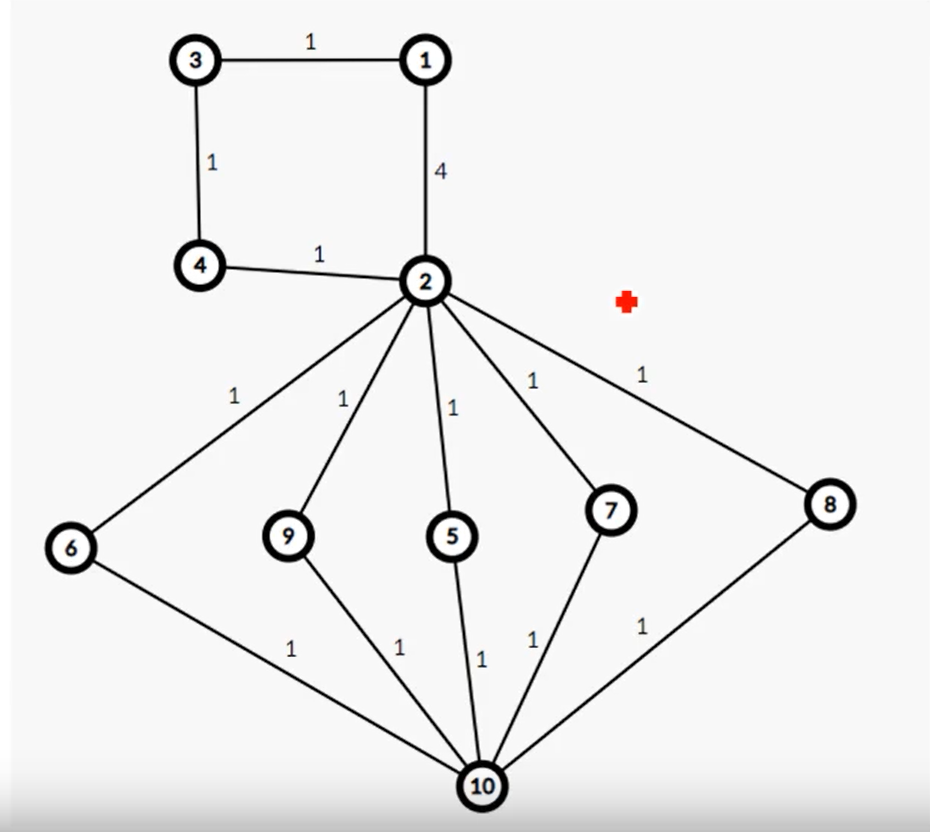
最短路算法分为两大类：

单源最短路(一个点到任意某个点或固定某个点)，常用算法有：
(1) $dijkstra$，只有所有边的权值为正时才可以使用。在稠密图上的时间复杂度是 $O(n^2)$，稀疏图上的时间复杂度是 $O(mlogn)$。
(2) $spfa$，不论边权是正的还是负的，都可以做。算法平均时间复杂度是 $O(km)$，k 是常数。
注意：在网格图中，spfa算法的效率比较低，如果边权为正，则尽量使用 dijkstra 算法
多源最短路，(任意两个点之间)一般用$floyd$算法。代码很短，三重循环，时间复杂度是 $O(n^3)$。

SPFA算法 P4779 【模板】单源最短路径

算法描述：
起点开始，周围若距离有更新(变短)，就更新距离
(若被更新点不在队列里，就记被更新点入列)

时间复杂度 :
平均情况下 $O(m)$，最坏情况下$ O(nm)$, $n$ 表示点数，$m$ 表示边数

模板：(参考作者：yxc)

void add(int a, int b, int c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int n;      // 总点数
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储每个点到1号点的最短距离
bool st[N];     // 存储每个点是否在队列中

// 求1号点到n号点的最短路距离，如果从1号点无法走到n号点则返回-1
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])     // 如果队列中已存在j，则不需要将j重复插入
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

完整代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;//存储到哪里，权值是多少
vector<pll> g[100005];
ll n,m,s;
queue <ll> q;
int dis[100005];//存储从start到i的最短路 
int vis[100005];//判断该点有没有在队列里

void spfa(){
    memset(dis,0x3f,sizeof(dis));//求最小值先赋值为无穷 
    dis[s]=0;
    q.push(s);
    vis[s]=1;

    while(!q.empty()){
        ll now=q.front();
        q.pop();//弹出元素(删除)
        vis[now]=0;//出列 就变成0  
        for(auto to:g[now]){
            ll w=to.second,v=to.first;//se权值，fir到哪里 
            if(dis[now]+w<dis[v]){//更短的话就更新 
            dis[v]=dis[now]+w;
            if(vis[v]==0){
                q.push(v);
                vis[v]=1;
            } 
        }
    }
}
}
int main(){
    scanf("%ld %ld %ld",&n,&m,&s);
    ll u,v,w;
    for(int i=1;i<=m;i++){
        scanf("%ld %ld %ld",&u,&v,&w);
        g[u].push_back({v,w});
    }
    spfa();
    for(int i=1;i<=n;i++){
        printf("%ld%c",dis[i],(i == n)?'\n':' ');
    }


    return 0;
} 

dijkstra算法 P4779 【模板】单源最短路径）

算法描述：
不再将相邻编号加入队列
而是将相邻的编号和距离都加入队列，每次取距离最小的点

邻接表
typedef pair<int,int> PII;
const int N = 100010, M = 200010;

int n,m,k;
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];

void add(int a, int b, int c)  // 添加一条边a->b，边权为c
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dijkstra()  // 求1号点到n号点的最短路距离
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
}

完整代码：

#include<bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;
const int N =10010;
int n,m,start;
int dist[N],vis[N];

vector<PII> g[N];
priority_queue<PII,vector<PII>,greater<PII> > q;//优先队列

void dijkstra(){
    memset(dist,0x3f,sizeof(dist));
    dist[start] = 0;
    q.push({0,start});// 求1号点到n号点的最短距离，如果不存在，则返回-1

    while(q.size()){
        int now = q.top().second;//开始点 
        q.pop();
        if(vis[now]) continue;//每个点会入队一次且是最小距离
        vis[now] = 1;

        for(auto to:g[now]){
            int v = to.second,w = to.first;
            if(dist[v]>dist[now]+w){
                dist[v] = dist[now]+w;
                q.push({dist[v],v});
            }

        } 
    }
}
int main(){
    cin >> n >> m >> start;
    for(int i =1;i<=m;i++){
        int x,y,z;
        cin >> x>> y >>z;
        g[x].push_back({z,y});//先权值再连接的点 
    }

    dijkstra();
    for(int i=1;i<=n;i++){
        cout<<dist[i]<<" ";
    } 

    return 0;
}

floyd算法：

利用其它点进行中转来求最短路

初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

完整代码：

#include<iostream>
using namespace std;
const int N=210,INF=0x3f3f3f3f;
int n,m,Q;
int d[N][N];
void floyd() {
    for(int k=1;k<=n;k++) {
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++) {
                d[i][j]=min(d[i][j], d[i][k]+d[k][j]);
            }
        }
    }
}
int main() {
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i==j) d[i][j]=0;
            else d[i][j]=INF;
    for(int i=0;i<m;i++) {
        int a,b,w;  cin>>a>>b>>w;
        // 处理重边 
        d[a][b]=min(d[a][b],w);
    }
    floyd(); 
    if(d[1][n]>INF/2) puts("impossible");
    else cout<<d[1][n]<<endl;
    return 0;
}

例题：P1119 灾后重建

#include<cstdio>
#include<cstring>
#include<iostream>
const int N = 210;//210个点
const int M = 50005; 
using namespace std;
int n,m,dis[N][N],t[M],q,k;
int main()
{
    scanf("%d%d",&n,&m);
    memset(dis,0x3f,sizeof(dis));
    memset(t,0x3f,sizeof(t));
    for(int i=0;i<n;i++)
     scanf("%d",&t[i]),//依次输入每一个村庄建立完成时需要的时间
      dis[i][i]=0;//自己到自己赋值为 0 
    for(int i=1;i<=m;i++)
     {
         int a,b,c;
         scanf("%d%d%d",&a,&b,&c);
         dis[a][b]=dis[b][a]=c;//邻接矩阵初始化权值
     }
    scanf("%d",&q);
    for(int o=1;o<=q;o++)
     {
         int a,b,c;
         scanf("%d%d%d",&a,&b,&c);
         while(t[k]<=c)
          {
              for(int i=0;i<n;i++)
               for(int j=0;j<n;j++)
                dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
              k++;
          }
        if(dis[a][b]==0x3f3f3f3f||t[a]>c||t[b]>c) printf("-1\n");
         else printf("%d\n",dis[a][b]);
     }
    return 0;
}

补充[数组模拟邻接表]： 输出最短路径端点

#include<bits/stdc++.h>
using namespace std;

const int N = 1010, M = 1010;

int h[N], e[M], w[M], nxt[M], eidx;

void add(int u, int v, int weight)   // 添加有向边 u->v, 权重为weight
{
    e[eidx] = v;        // 记录边的终点
    w[eidx] = weight;   // 记录边的权重
    nxt[eidx] = h[u];   // 将下一条边指向结点u此时的第一条边
    h[u] = eidx;        // 将结点u的第一条边的编号改为此时的eidx
    eidx++;             // 递增边的编号edix, 为将来使用
}
void iterate(int u)   // 遍历结点u的所有邻边
{
    // 从u的第一条边开始遍历，直到eid==-1为止
    for(int eid = h[u]; eid != -1; eid = nxt[eid])
    {
        int v = e[eid];
        int weight = w[eid];
        cout << u << "->" << v << ", weight: " << weight << endl;
    }
}

int main()
{
    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);  // 初始化h数组为-1
    eidx = 0;                 // 初始化边的编号为0

    while(m--)
    {
        int u, v, weight;
        cin >> u >> v >> weight;
        add(u, v, weight);
    }

    for(int u = 1; u <= n; ++u)
        iterate(u);

    return 0;
}

/*
4 6 
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
*/ 
输出结果：[逆序]
1->4, weight: 4
1->3, weight: 5
1->2, weight: 2
2->4, weight: 1
2->3, weight: 2
3->4, weight: 3