线段树

书接上文，最后一道题差点弄晕，对不对，所以这次别慌，有更好的方法。

线段树基于分治思想。啥意思呢？

这里有一段可爱的区间。

表示的是$1-8$。

那么接下来我们对这个区间进行一些操作：

这个不难办，直接改就行了。

但接下来这个呢？

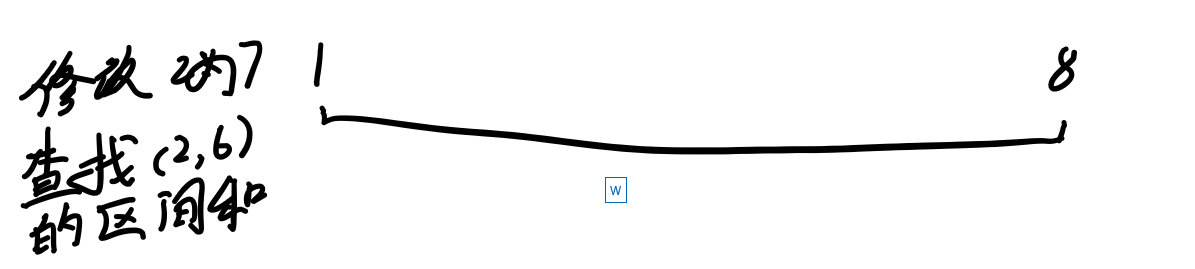
考虑修改运算，如果直接建数组的话可以$O(1)$维护，直接a[x] = v就行了。

但是查询运算就是费劲了。

这样的话我们需要遍历，o(N)有点毒瘤。

我们还可以用前缀和优化，但好像也每快多少。

接下来先别慌，虽然后面有点高能，先回忆一下这个。

然后我们突然想到分治思想。

分治的话在很多算法中都有用到，是非常常用而且非常简单的一种算法。

可以从字面上来理解，就是“分而治之”的意思。

那么我们可以把每一个区间一分为二，这样就把整个区间变成了一棵树。

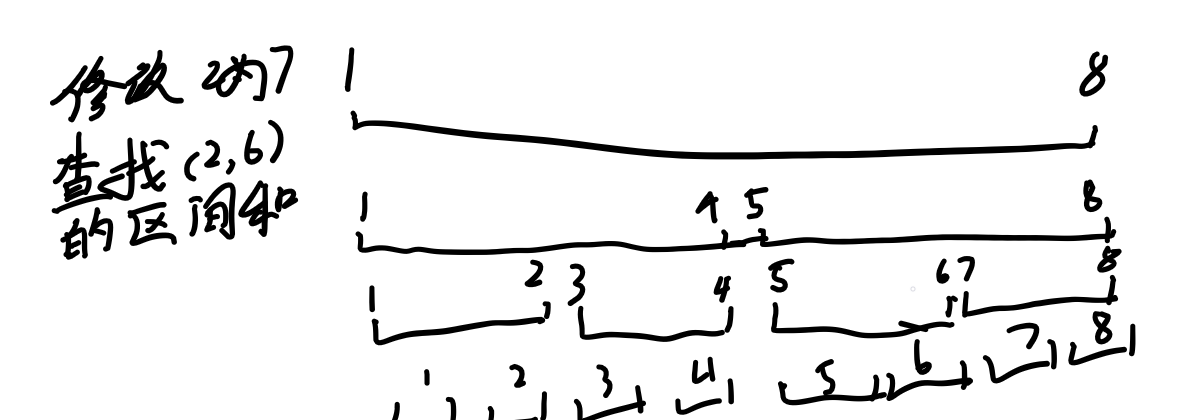
这样的话我们可以看一下两个操作，因为是树上，而且是一棵满二叉树，所以深度一定是$O(log N)$的。

这样两个操作都是logn了，秀到飞起。

所以说这样就好了呀~

我们来看一些基本的操作吧！

首先是上传的操作，线段树的意思就是用左右子树更新根节点。

这个操作有名字，叫pushup。

怎么写呢？

这个的话我们结合着拿到题写吧。

就是单点修改，区间查询。

线段树的话一般使用结构体维护。

结构体里想要啥有啥放进去就行了。

struct Node
{
    int l, r;//左右端点区域

    int sum;//各种查询变量存储区域

    //最后还有个懒标记区域，一般在区间修改时使用。
}tr[N * 4];//4倍空间

那么的话pushup的操作就是用左右两边的区间更新总区间。

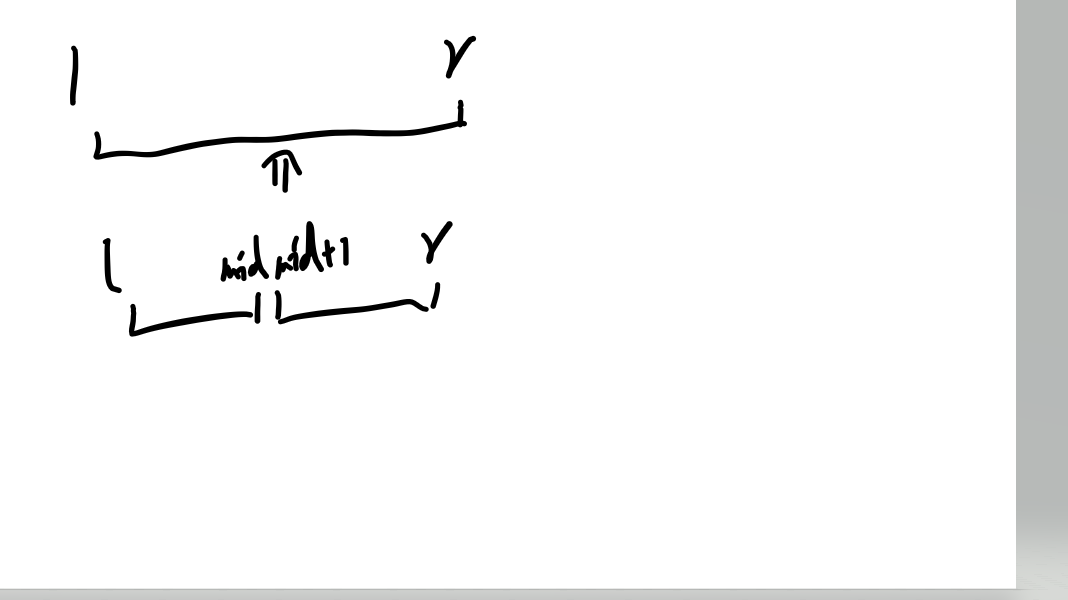
这个的话很简单，大区间等于小区间的和。

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

然后就是建树操作，在最开始需要把树“建造出来”。

这个可以直接递归建立树。

这个的话可以分治处理。

先用一张图分析一下吧。

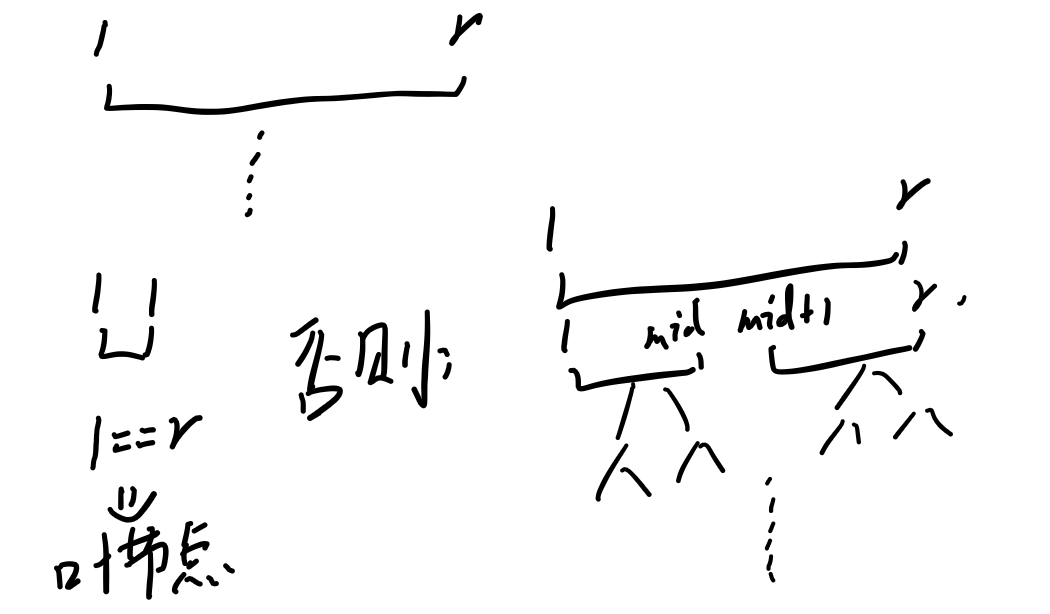
那么的话我们试着捋一下逻辑。

首先的话是判断一下是否是叶节点。

否则的话就分段处理就行。

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

然后就是变化操作和查询操作。

变化操作就是直接搜就行了。

这个跟build很类似，没有什么太大的难度，而且是单点修改，很水哦。

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

然后是查询操作。

这个也不难。

就可以直接判断区间。

那么的话我们来康一下代码吧：

int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if(l <= mid) v = query(u << 1, l, r);
    if(r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

我这里背的一直是y总的板子，也向大家推荐一下，码风非常优美，但又不失简洁明了。

然后基本就能稍微弄几道题了。

1

这道题是维护动态区间最大值。

那么的话只要稍微改一下板子就行了，记得记录n来表示这个长度。

在最后添加一个数可以理解成把这个数改成就行了。

查询操作没什么好说的，这个直接套上板子就行了。

这个题就是稍微有一点点绕的，我们来看一下。

#include<bits/stdc++.h>
using namespace std;
const int N = 200010;
int m, p;
struct Node
{
    int l, r;
    int v;
}tr[N * 4];
void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);//pushup操作
}
int query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v;//下面的是板子
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if(l <= mid) v = query(u << 1, l, r);
    if(r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}
void modify(int u, int x, int v)
{
    if(tr[u].l == x && tr[u].r == x) tr[u].v = v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}
void build(int u,  int l, int r)
{
    tr[u] = {l, r};
    if(l == r) return ;
    int mid =l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}
int main()
{
    int n = 0, last = 0;//last表示最后一个数，n表示长度
    cin >> m >> p;
    build(1, 1, m);
    int x;
    string op;
    while(m --)
    {
        cin >> op >> x;
        if(op == "Q")
        {
            last = query(1, n - x + 1, n);//输出结果，从长度开始到n
            cout << last << endl;//最后输出最后的最大值
        }
        else
        {
            modify(1, n + 1, (last + x) % p);//添加一个数
            n ++;
        }
    }
}

2

稍微有一点难。

这个的话我们可以利用一个小技巧。

可以同tmax表示答案，记录sum表示和。

更新这两个的时候记得维护一个lmax和rmax表示最大前缀和后缀。

然后更新的时候就是pushup绕一点点。

具体你们看看代码吧， 我觉得还是比较好理解的，剩下的话和普通线段树的板子一模一样。

#include<bits/stdc++.h>
using namespace std;
const int N = 500010;
int n, m;
int w[N];
struct Node
{
    int l, r;
    int sum;
    int lmax, rmax, tmax;
}tr[N * 4];
void push_up(Node &u, Node &l, Node &r)//太长了，单独弄出一个函数
{
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tmax = max(max(r.tmax, l.tmax), l.rmax + r.lmax);
}
void pushup(int u)
{
    push_up(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r)
{
    if(l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}
void change(int u, int x, int v)
{
    if(tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) change(u << 1, x, v);
        else change(u << 1 | 1, x, v);
        pushup(u);
    }
}
Node query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(r <= mid) return query(u << 1, l, r);
        else if(l > mid) return query(u << 1 | 1, l, r);
        else
        {
            Node ql = query(u << 1, l, r);
            Node qr = query(u << 1 | 1, l, r);
            Node ans;
            push_up(ans, ql, qr);
            return ans;
        }
    }
}
int main()
{
    cin >> n;
    cin >> m;
    for(int i = 1; i <= n; i ++) cin >> w[i];
    build(1, 1, n);
    while(m --)
    {
        int op, x, y;
        cin >> op >> x >> y;
        if(op == 1)
        {
            if(x > y) swap(x, y);
            cout << query(1, x, y).tmax << endl;
        }
        else
        {
            change(1, x, y);
        }
    }
    return 0;
}

3

大家一看，哎，这不是个懒标记的板子题吗？

这道题当然可以用懒标记做，但我们还没聊到那里。

如果你不会懒标记可以乱搞差分。

差分的作用就是处理区间加减，这里就是一个线段树上差分了。

对与差分数组的维护，我们就可以把第一个操作看成两个单点修改的操作，这不就简单了？

然后求区间最大公约数的时候也是一样，跟板子差不多。

但是要注意一些逻辑处理问题，稍有不慎就能把你调试到挂。

关于调试建议大家出门右转去看我的维护序列那个文章的题解，有线段树debug指南！

#include<bits/stdc++.h>
using namespace std;
const int N = 500010;
#define ll long long
int n, m;
ll w[N];
struct Node
{
    int l, r;
    ll sum;
    ll d;
}tr[N * 4];
ll gcd(ll a, ll b)
{
    return b ? gcd(b, a % b) : a;//gcd，必不可少
}
void push_up(Node &u, Node &l, Node &r)
{
    u.sum = l.sum + r.sum;
    u.d = gcd(l.d, r.d);//对与两个进行更新
}
void pushup(int u)
{
    push_up(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
void build(int u, int l, int r)
{
    if(l == r) 
    {
        ll sub = w[r] - w[r - 1];//差分一波
        tr[u] = {l, r, sub, sub};
    }

    //板子区
    else
    {
        tr[u].l = l, tr[u].r = r;
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}
void change(int u, int x, ll v)
{
    if(tr[u].l == x && tr[u].r == x)
    {
        ll b = tr[u].sum + v;
        tr[u] = {x, x, b, b};
    }
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(x <= mid) change(u << 1, x, v);
        else change(u << 1 | 1, x, v);
        pushup(u);
    }
}
Node query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) 
    {
        return tr[u];
    }
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(r <= mid) return query(u << 1, l, r);
        else if(l > mid) return query(u << 1 | 1, l, r);
        else
        {
            Node left = query(u << 1, l, r);
            Node right = query(u << 1 | 1, l, r);
            Node res;
            push_up(res, left, right);
            return res;
        }
    }
}
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i ++) cin >> w[i];
    build(1, 1, n);// 千万别忘
    while(m --)
    {
        char op;
        int l, r;
        ll d;
        cin >> op;
        if(op == 'C')
        {
            cin >> l >> r >> d;
            change(1, l, d);
            if(r + 1 <= n) change(1, r + 1, -d);//进行差分的时候又坑，小心点
        }
        else
        {
            cin >> l >> r;
            Node left = query(1, 1, l);
            Node right = {0, 0, 0, 0};
            if(l + 1 <= r) right = query(1, l + 1, r);//这里也有一个坑，差点没把我给搞挂
            cout << abs(gcd(left.sum, right.d)) << endl;//最后输出答案，一定要加abs
        }
    }
    return 0;
}

懒标记与区间修改。

区间修改时我们发现一次次开来回回加，太**慢了。

所以的话为了减少毒瘤程度和时间复杂度，对与每个线段，引入一个懒标记表示更改的值的和。

懒标记的性质是可叠加性，这个一会再说。

然后懒标记是运用pushdown的分裂处理操作来更新的。

好先看板子题，然后根据题目分析。

4

报仇，来了。

首先就是区间修改区间查询。

让我们看一看pushdown，首先你得把根节点的懒标记更新到下面，然后还要把懒标记清空。

真的是一个复杂的过程。

然后的话我们看一下这个的代码。

void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if(root.add != 0)
    {
        left.add += root.add;
        right.add += root.add;
        left.sum += (ll) (left.r - left.l + 1) * root.add;
        right.sum += (ll) (right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

注意此时在定义结构体的时候要加一个懒标记区域。

struct Node
{
    int l, r;
    ll sum, add;//sum是记录，add是懒标记
}tr[N * 4];

然后我们来看一下改变。

首先的话build没有大变化，大家看一下。

void build(int u, int l, int r)
{
    if(l == r)
    {
        tr[u] = {l, r, w[r], 0};//初始时懒标记初始成0！
    }
    else
    {
        tr[u] = {l, r};
        int mid = (l + r ) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

query和change记得要分裂处理。

void change(int u, int l, int r, int d)
{
    if(tr[u].l >= l && tr[u].r <= r) 
    {
        tr[u].sum += (ll) (tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    }
    else
    {
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) change(u << 1, l, r, d);
        if(r > mid) change(u << 1 | 1, l, r, d);
        pushup(u);
    }
}
ll query(int u, int l, int r)
{
    if(tr[u].l >= l &&tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) >> 1;
    ll sum = 0;
    if(l <= mid) sum += query(u << 1, l, r);
    if(r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

不开 longlong 见祖宗

然后的话就是本题的完整代码了：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
#define ll long long
int n, m;
int w[N];
struct Node
{
    int l, r;
    ll sum, add;
}tr[N * 4];
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{
    Node &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if(root.add != 0)
    {
        left.add += root.add;
        right.add += root.add;
        left.sum += (ll) (left.r - left.l + 1) * root.add;
        right.sum += (ll) (right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}
void build(int u, int l, int r)
{
    if(l == r)
    {
        tr[u] = {l, r, w[r], 0};
    }
    else
    {
        tr[u] = {l, r};
        int mid = (l + r ) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}
void change(int u, int l, int r, int d)
{
    if(tr[u].l >= l && tr[u].r <= r) 
    {
        tr[u].sum += (ll) (tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    }
    else
    {
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) change(u << 1, l, r, d);
        if(r > mid) change(u << 1 | 1, l, r, d);
        pushup(u);
    }
}
ll query(int u, int l, int r)
{
    if(tr[u].l >= l &&tr[u].r <= r) return tr[u].sum;
    pushdown(u);
    int mid = (tr[u].l + tr[u].r) >> 1;
    ll sum = 0;
    if(l <= mid) sum += query(u << 1, l, r);
    if(r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> w[i];
    build(1, 1, n);
    while(m --)
    {
        int l, r, d;
        char op;
        cin >> op;
        if(op == 'C')
        {
            cin >> l >> r >> d;
            change(1, l, r, d);
        }
        else 
        {
            cin >> l >> r;
            cout << query(1, l, r) << endl;
        }
    }
    return 0;
} 

5

又是一个套路提或者板子题。

一看，哎，求总面积。

这怎么和线段树有关系？

俗话说的好：

有办法就用办法，没有办法就创造办法！！

很多都是这样，以后的树链剖分不也是一样吗？

所以的话我们要可以吧这个图一点一点向左移动。

也可以理解成用一条线从左到右一路扫过去。

这条线就叫扫描线。

我们可以把扫描线扫过的图形的地方看成区间+1操作，结束时看成-1操作，然后就变成了统计最长的大于0的数的长度。

这样的话就是一个完美的线段树了。

注意这里有一个小小的套路，就是说不用pushdown也可以AC。

所以的话没有什么特别难的。

等等，海没有结束。

这个数据稍微有亿点点大啊！

怎么办？

首先，不要慌张，直接使用离散化。

但是代码太长了，于是lower_bound它来了！！！

离散化直接用vector就香了。

完美。

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
struct sg
{
    double x, y1, y2;
    int k;
    bool operator< (const sg &t)const
    {
        return x < t.x;
    }
}seg[N * 2];
struct Node
{
    int l, r;
    int cnt;
    double len;
}tr[N * 8];
vector<double> ys;
int find(double y)
{
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}
void pushup(int u)
{
    if(tr[u].cnt)//板子区
    {
        tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
    }
    else if(tr[u].l != tr[u].r)
    {
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    }
    else tr[u].len = 0;
}
//不用pushdown就很香
void build(int u, int l, int r)
{
    tr[u] = {l, r, 0, 0};
    if(l != r) 
    {
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
    }
}
void change(int u, int l, int r, int k)
{
    if(tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += k;
        pushup(u);
    }
    else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) change(u << 1, l, r, k);
        if(r > mid) change(u << 1 | 1, l, r, k);
        pushup(u);
    }
}
int main()
{
    int t = 1;
    while(cin >> n, n)
    {
        ys.clear();
        for(int i = 0, j = 0; i < n; i ++) 
        {
            double x1, y1, x2, y2;
            cin >> x1 >> y1 >> x2 >> y2;
            seg[j ++] = {x1, y1, y2, 1};
            seg[j ++] = {x2, y1, y2, -1};
            ys.push_back(y1);
            ys.push_back(y2);
        }
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());//离散化排序去重
        build(1, 0, ys.size() - 2);
        sort(seg , seg + n * 2);
        double res = 0;
        for(int i = 0; i < n * 2; i ++)
        {
            if(i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
            change(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
        }
        cout << "Test case #" << t ++ << endl;//多组样例非常坑人，小心啊
        cout << "Total explored area: ";
        printf("%.2lf\n", res);
        cout << endl;
    }   
    return 0;
} 

6

最后一道题，大家坚持一下。

这道题的话别慌，一看是两个操作。

第一反应就是开两个懒标记。

接着考虑到两个问题：

1. 这破更新好像能写死人
2. 这懒标记先加后乘还是先乘后加啊

第一个问题只是个吐槽。

没辙，硬钢就行了。

第二个然后一看就是先加后乘，诶，不行啊，有bug！！

但是换一下，哎，这个先乘后加就行了。

这说明什么啊？

想到前面的可叠加性了吗？

是不是恍然大悟？？

所以的话这不就秒了吗？

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define ll long long 
int n, p, m;
int w[N];
struct Node
{
    int l, r;
    int add, sum, malt;//建立线段树节点，sum表示区间和，l, r废话少说，add和malt是懒标记
}tr[N * 4];//懒标记和这个维护的sum要有可叠加性，所以选择了先乘再加
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    tr[u].sum = tr[u].sum % p;//更新这个sum，没啥好说的
}
void pushdown(int u)
{
    tr[u << 1].sum = ((ll)tr[u << 1].sum * tr[u].malt + (ll)tr[u].add * (tr[u << 1].r - tr[u << 1].l + 1)) % p;
    tr[u << 1 | 1].sum = ((ll)tr[u << 1 | 1].sum * tr[u].malt + (ll) tr[u].add * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1)) % p;
    tr[u << 1].add = ((ll)tr[u << 1].add * tr[u].malt + tr[u].add) % p;
    tr[u << 1 | 1].add = ((ll)tr[u << 1 | 1].add * tr[u].malt + tr[u].add) % p;
    tr[u << 1].malt = (ll)tr[u << 1].malt * tr[u].malt % p;
    tr[u << 1 | 1].malt = (ll)tr[u << 1 | 1].malt * tr[u].malt % p;//先乘再加，然后取模，注意longlong，不然就像我第一次搞的时候一样建祖宗了
    tr[u].add = 0;//最后记得清空懒标记
    tr[u].malt = 1;//乘法的懒标记一定是1，不然就全都0了
}
void build(int u, int l, int r)//开始建树
{
    if(l == r) tr[u] = {l, r, 0, w[r], 1};//只要是叶节点的话就直接建立，sum自然是w[r]，当然写w[l]也行
    else
    {
        tr[u] = {l, r, 0, 0, 1};//乘法懒标记搞成1
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);//build左右两边
        build(u << 1 | 1, mid + 1, r);
        pushup(u);//最后记得上传，build是一层层往下的，不用分裂处理，也就是不用pushdown
    }
}
void change(int u, int l, int r, int malt, int add)//改变函数，我习惯change
{
    if(tr[u].l >= l && tr[u].r <= r)//如果包含在区间内部
    {
        //改变懒标记和sum，先乘后加！！！注意开long long
        tr[u].sum = ((ll)tr[u].sum * malt + (ll)add * (tr[u].r - tr[u].l + 1)) % p;
        tr[u].add = ((ll)tr[u].add * malt + add) % p;
        tr[u].malt = (ll)tr[u].malt * malt % p;
    }
    else//分裂处理，先pushdown
    {
        pushdown(u);//处理懒标记
        int mid = (tr[u].l + tr[u].r) >> 1;//算一下终点
        if(l <= mid) change(u << 1, l, r, malt, add);//算左右两边
        if(r > mid) change(u << 1 | 1, l, r, malt, add);
        pushup(u);//合并一下，然后处理sum
    }
}
int query(int u, int l, int r)//查询操作
{
    if(tr[u].l >= l && tr[u].r <= r)
    {
        return tr[u].sum;//如果在区间之内直接返回
    }
    pushdown(u);//这个跟修改很像，也先分裂一下，处理懒标记
    int mid = (tr[u].l + tr[u].r) >> 1;//处理左右两边
    ll res = 0;//开个res记录
    if(l <= mid) 
    {
        res += query(u << 1, l, r);
        res = res % p;//取模不要忘啊
    }
    if(r > mid) 
    {
        res += query(u << 1 | 1, l, r);
        res = res % p;
    }
    return res;
}
int main()
{
    cin >> n >> p;//读入没啥好说的
    for(int i = 1; i <= n; i ++) cin >> w[i];
    build(1, 1, n);//记得建树，不然就凉了
    cin >> m;
    while(m --)
    {
        int op;
        int l, r;
        int c;
        cin >> op;
        if(op == 2)
        {
            cin >> l >> r >> c;
            change(1, l, r, 1, c);//这个我写的是加法，你们可以改一下
            //加法相当于*1+c，不能把malt制成0，我这么干了，结果答案成了00000。。。
        }
        else if(op == 1)
        {
            cin >> l >> r >> c;
            change(1, l, r, c, 0);//一样，*c+0
        }
        else
        {
            cin >> l >> r;
            cout << query(1, l, r) << endl;//查询操作
        }
    }
    return 0;//愉快结束
}

看一下海有一点距离啊，于是再加上一点debug指南吧。

一般写完会CE不多说了。

然后总结几个SF的问题：首先先看一下自己开没开4倍空间，注意四倍指的并不是N的四倍，而是维护区间长度的4倍。

这是个大坑，具体请出门左转查看亚特兰蒂斯那道题。

然后就是看看自己有没有把l和tr[u].l搞混，不要乱，建树的时候一般用l，其他时候用另一个。

如果还调试不出来，那可能就位运算写错了，好好看看吧。

如果位运算也没问题，那就得看看逻辑上有没有错误了。

SF调完一般调WA。

WA的话先看看开没开long long，我就因为没开ll卡了10分钟。

然后就是看看有没有明显的逻辑错误，这时候建议肉眼调试。

最后如果还不行可以输出一下tr数组的变动，看看是不是pushdown的逻辑处理错了。

然后是TLE，首先看看有没有什么可以优化的，举几个例子：

前缀和：查询区间和时可以使用

差分：区间加法时能用，具体可以出门左转，去看区间最大公约数那道题。

二分：优化查找部分，一般和离散化配套使用。

离散化：具体不多说了，还是那句话，出门左拐，去看亚特兰蒂斯那道题。

dp：线段树优化dp，很难了，去学闫式dp分析法吧。

好了如果你海没有debug出来。那我也没办法了。

好了这就是今天的blog

是除夕更新的，祝大家新年快乐！！

喜欢给个关注吧！

cht的全部分享

点赞+收藏过15，我就周更，点赞收藏过40，我就日更。

byebye~~（一千行）