思路
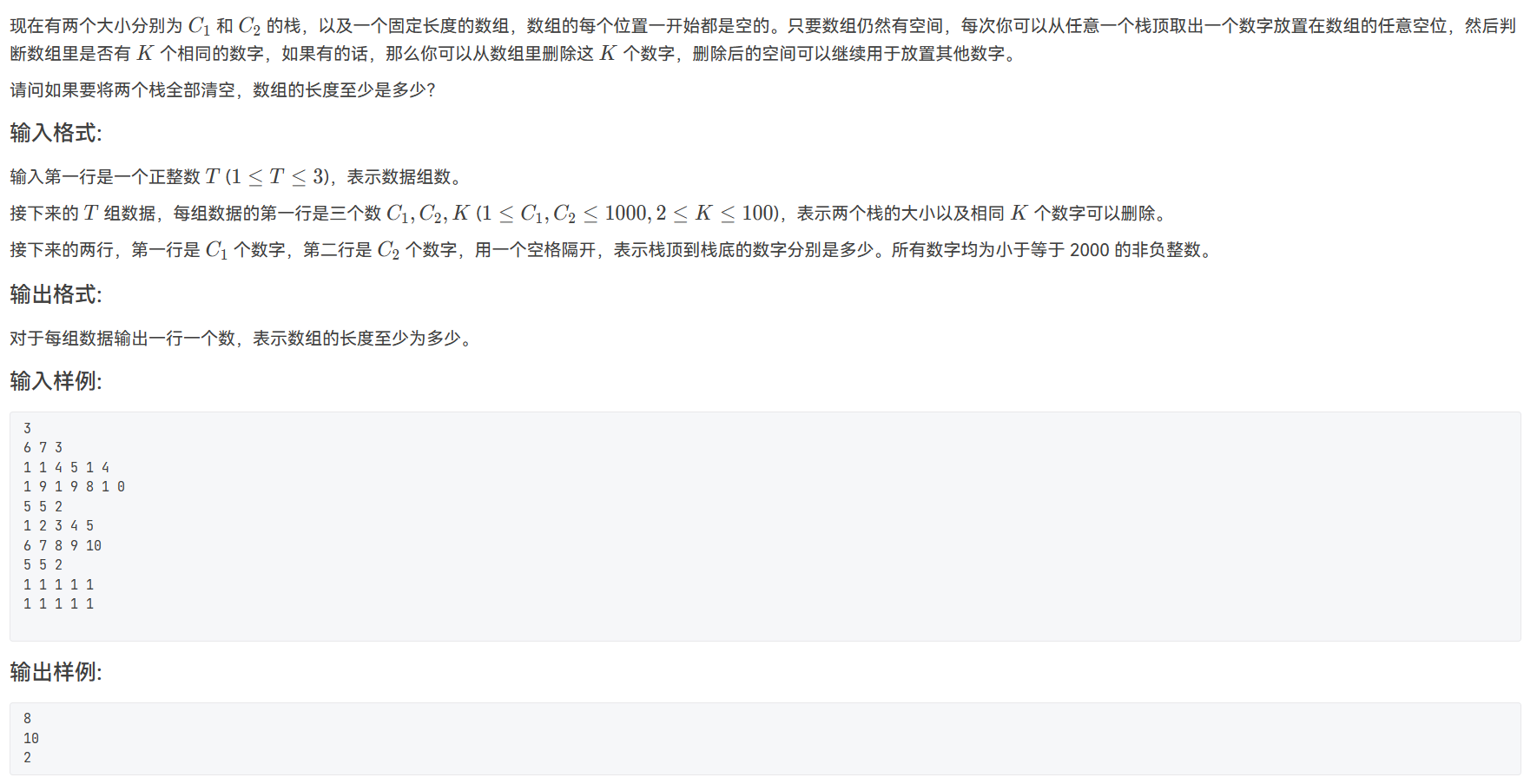
这题要求求最小值，且一个状态可以由前两个状态转移

状态表示
pii f[i][j]表示从C1栈拿了i个数字，从C2拿了j个数字后数组的历史最大容量为first，当前容量为second
状态计算
1.拿C1
f[i][j].sz=f[i-1][j].sz+1
f[i][j].cap=max(f[i][j].sz,f[i-1][j].cap) 因为最大容量要么在之前，要么最新最大
2.拿C2
f[i][j].size=f[i][j-1].sz+1
f[i][j].cap=max(f[i][j].sz,f[i][j-1].cap)
3.取最小
f[i][j]=min(f[i-1][j],f[i][j-1])

答案：f[n][m].cap

#include <bits/stdc++.h>
#define cap first
#define sz second
using namespace std;
typedef pair<int,int> pii;
const int inf=0x3f3f3f3f;
const int N=1010;
int a1[N],a2[N];

int main()
{
    int t;cin>>t;
    while(t--)
    {
        int n,m,k;cin>>n>>m>>k;
        for(int i=1;i<=n;i++)    cin>>a1[i];
        for(int i=1;i<=m;i++)    cin>>a2[i];

        vector<vector<pii>>f(n+1,vector<pii>(m+1,{inf,inf}));
        f[0][1]=f[1][0]={1,1};
        map<int,int>c1;
        for(int i=1;i<=n;i++){
            c1[a1[i]]++;
            map<int,int>c2;
            for(int j=1;j<=m;j++){
                c2[a2[j]]++;

                pii x,y;
                x.sz=f[i-1][j].sz+1;
                x.cap=max(x.sz,f[i-1][j].cap);
                if((c1[a1[i]]+c2[a1[i]])%k==0)  x.sz-=k;

                y.sz=f[i][j-1].sz+1;
                y.cap=max(y.sz,f[i][j-1].cap);
                if((c1[a2[j]]+c2[a2[j]])%k==0)  y.sz-=k;

                f[i][j]=min(x,y);
            }
        }
        cout<<f[n][m].cap<<endl;
    }



    return 0;
}