1、线段树简介
在很小的时间复杂度内实现单点修改、区间修改、区间查询（区间求和、求最大最小值、区间gcd等）
维护的信息需要满足区间加法，[l, r]维护的信息可以由[l, mid] 和[mid + 1, r]合并而来
主要操作

2、建树
对线段区间建树，不断二分区间，一维数组存整棵树
每一个区间表示一棵树，叶子结点表示的区间只有一个元素

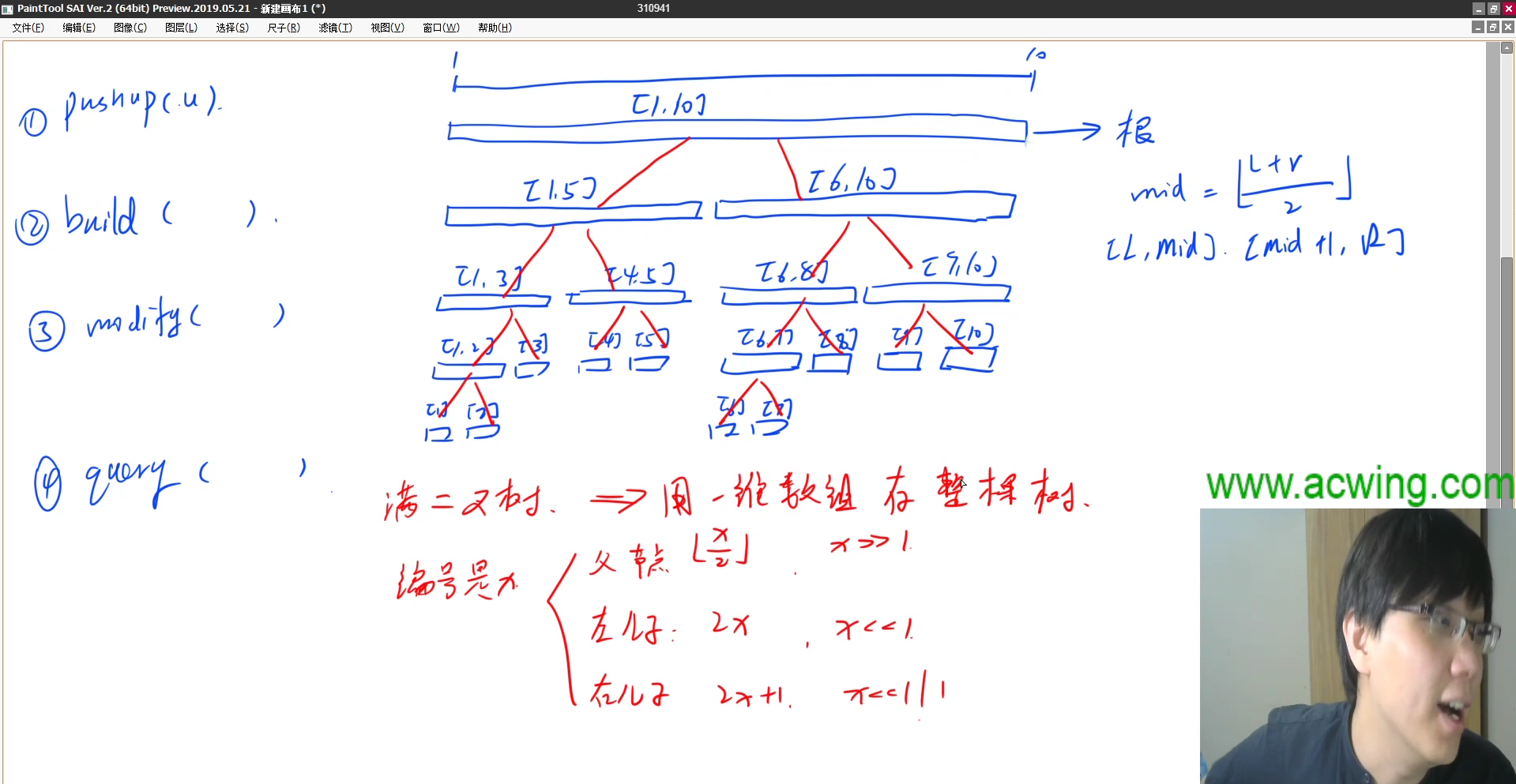
最后一层最多有2个结点，最坏情况下，最后一层最右边2个结点，最右下角编号2n-1 + 2n = 4n-1，所以线段树一般开4n的空间

build (int u, int L, intt R)
{
    tr[u].L = L, tr[u].R = R;
    if(L == R)return ;
    int mid = L + R >> 1;
    build(u << 1, L, mid);
    build(u << 1 | 1, mid + 1, R);
    pushup(u); //合并儿子信息
}

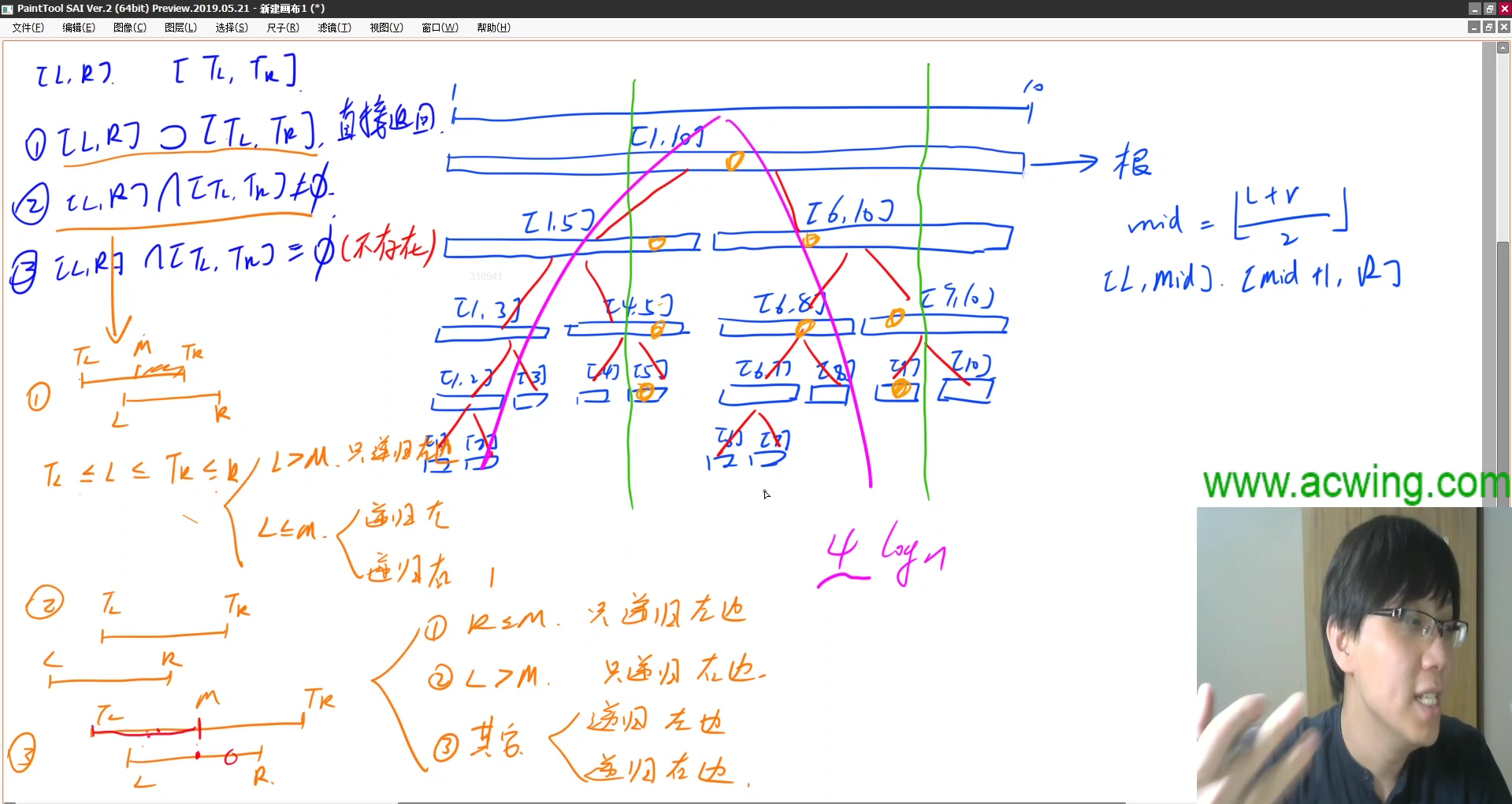
3、查询操作

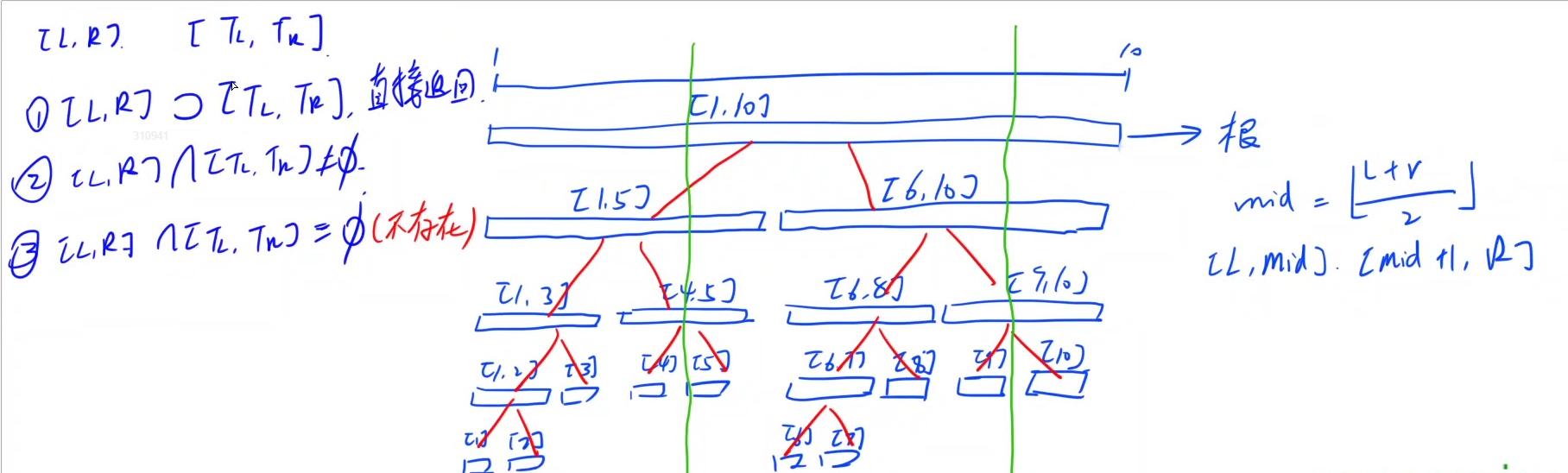
比如查询[5,9],
从根节点开始，
如果[5,9]包含[tl,tr]直接返回信息，如[6,8]
如果[5, 9]与[tl,tr]相交,递归找有交点的部分，如[4,5]递归[5]
不会出现相交为空的情况，因为每次递归都是找有交点的
时间复杂度o(logn)