最短路径问题

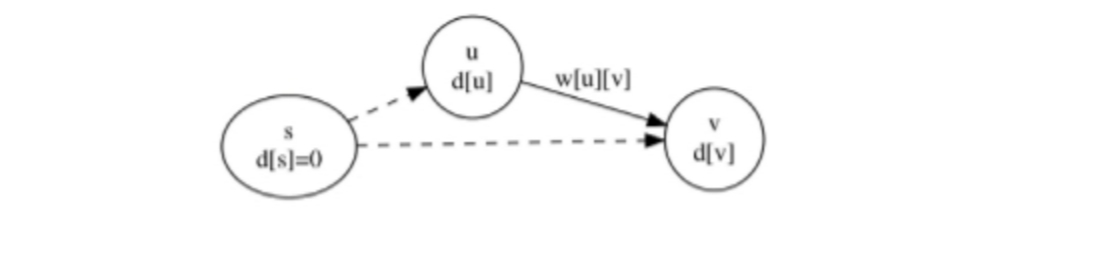
松弛操作

• 对于点 $v$，$d[v]$ 表示从源点 $s$ 出发，到 $v$ 点 目前已知的最短路径的长度
• $d[s] = 0$
• 如果存在一条边 $< u, v >$，则可以尝试通过这条边更新 $d[v]$
• 松弛操作：$d[v] = min(d[v], d[u] + w[u][v])$

松弛的数学性质

• 上界性质：设 $dis[v]$ 表示从 $s$ 点到 $v$ 点的最短路径的长度，则在算法运行的过程中 $dis[v] \leqslant d[v]$，且一旦 $d[v]$ 收敛到 $dis[v]$，就不会有改变。
• 三角不等式：对任意边 $< u, v > \in \rm E$，有 $dis[v] \leqslant dis[u] + w(u, v)$
• 无路径性质：若从 $s$ 到 $v$ 不存在路径，则总有 $d[v] = dis[v] = \infty$
• 收敛性质：如果图 $G$ 中边 $< u, v >$ 在 $s$ 到 $v$ 的最短路径上，考察路径 $s$ 到 $u$ 到 $v$，若算法中在松弛边 $< u, v >$ 之前的任何时间有 $d[u] = dis[u]$，则在操作过后总有 $d[v] = dis[v]$
• 路径松弛性质：如果 $p = < v_0, v_1, \cdots, v_k >$ 是从 $s = v_0$ 到 $v_k$ 的最短路径，而且 $p$ 中的边按照 $< v_0, v_1 > < v_1, v_2> \cdots < v_{k - 1}, v_k >$ 的顺序进行松弛，那么最后 $d[v_k] = dis[v_k]$。这个性质的保持并不受其他松弛操作的影响，即使他们与 $p$ 中边上的松弛操作混在一起。
• 最优子结构性质：若 $p = < v_1, v_2, \cdots, v_k >$ 是 $v_1$ 到 $v_k$ 的最短路径，对于其中的任意一段 $1 \leqslant i \leqslant j \leqslant k$，$p_{ij} = < v_i, \cdots, v_j >$ 必是 $v_i$ 到 $v_j$ 的最短路径。
• 如果存在一条从 $s$ 可达的负权回路，则 $s$ 到该回路上的顶点，以及回路后的所有顶点，不存在最短路径
• 最短路径上不包含环

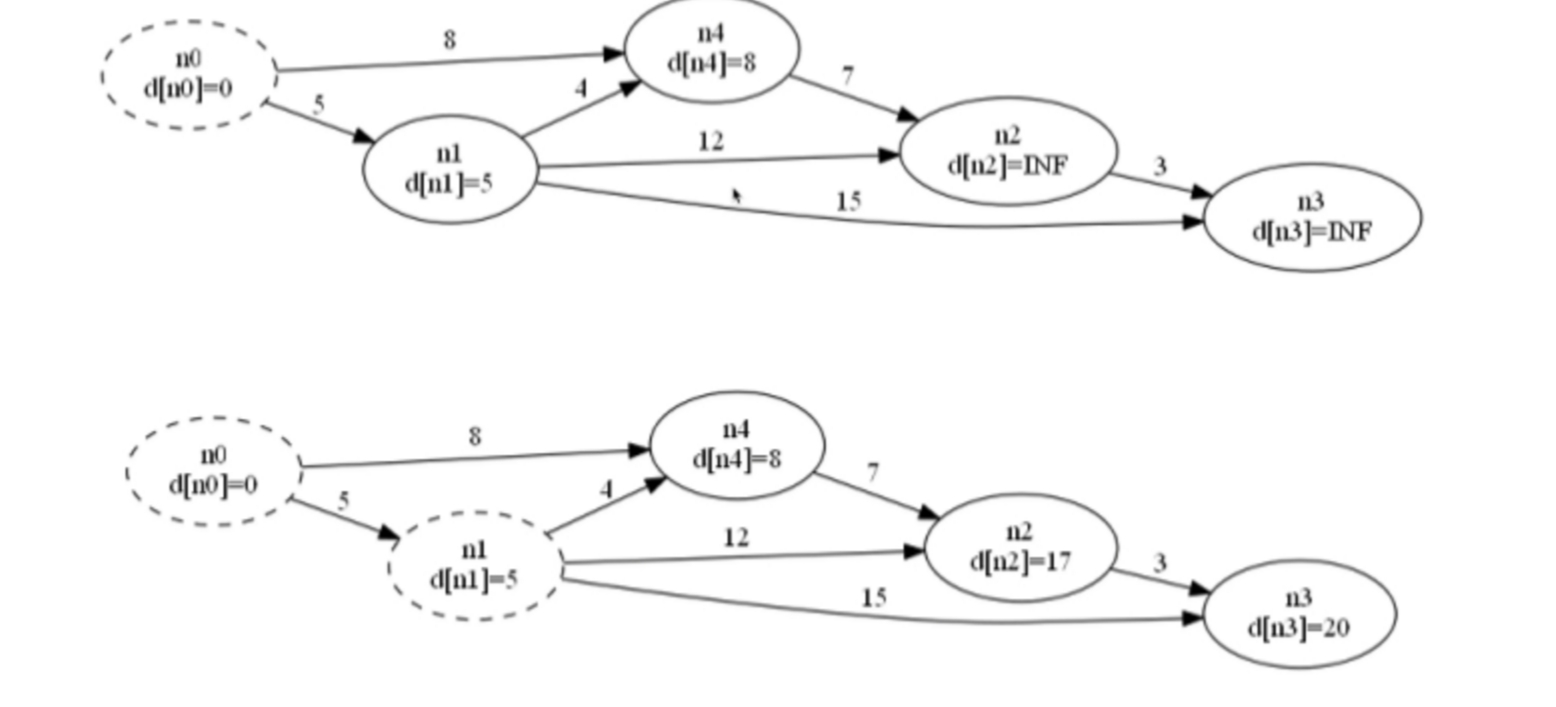
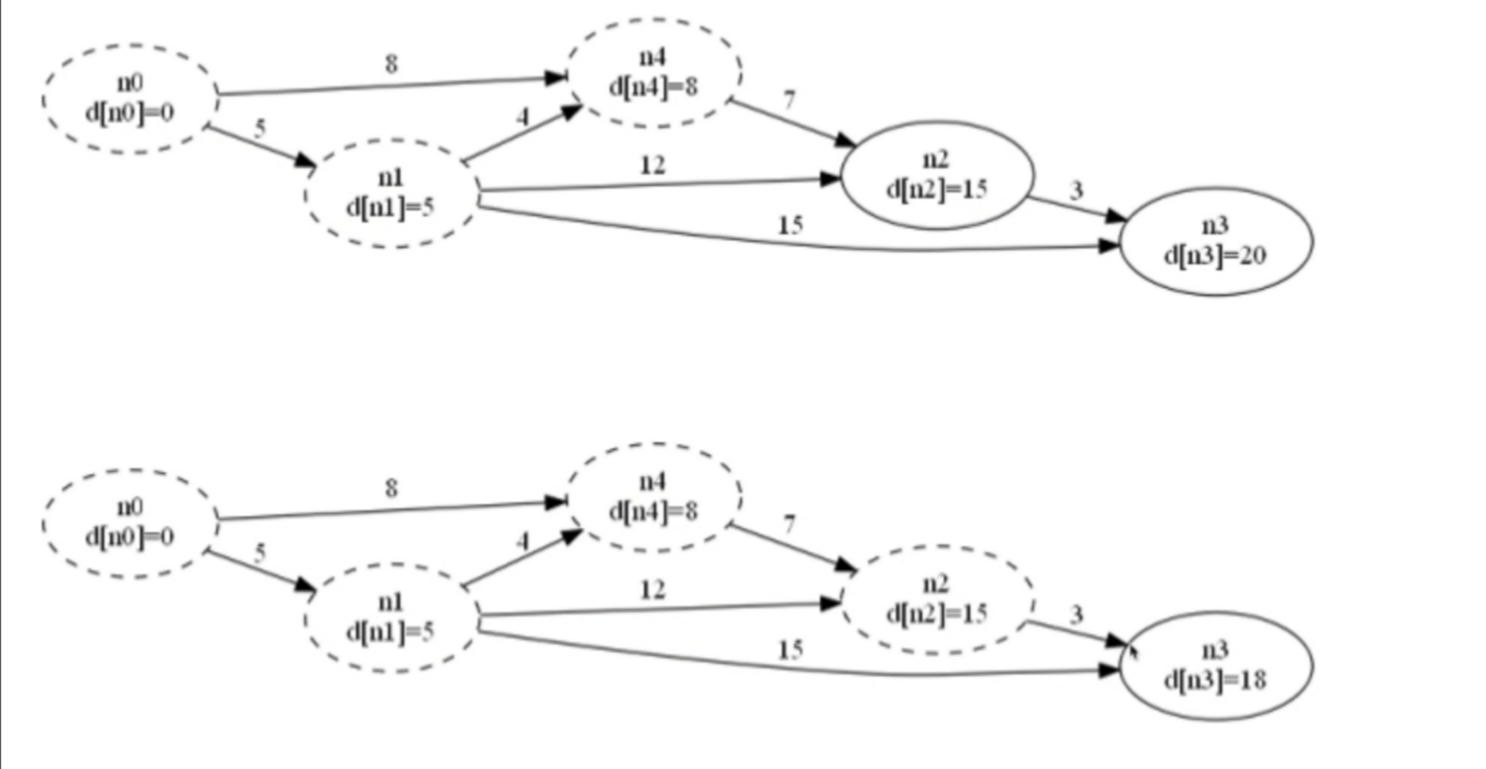
Dijkstra

$G = \{V, E\}$

1. 初始时令 $S = \{V_0\}$，$T = V - S = \{\text{其余顶点}\}$，$T$ 中顶点对应的距离值为 $d$。
   若存在 $< V_0, V_i >$，$d[V_i]$ 为 $< V_0, V_i >$ 弧上的权值
   若不存在 $< V_0, V_i >$，$d[V_i]$ 为 $\infty$
2. 从 $T$ 中选取一个与 $S$ 中顶点有关联边且权值最小的顶点 $W$，加入到 $S$ 中
3. 对其余 $T$ 中顶点的距离值进行修改：
   若加进 $W$ 作中间顶点，从 $V_0$ 到 $V_i$ 的距离值缩短，则修改此距离值

重复上述步骤2、3，直到 $S$ 中包含所有顶点。

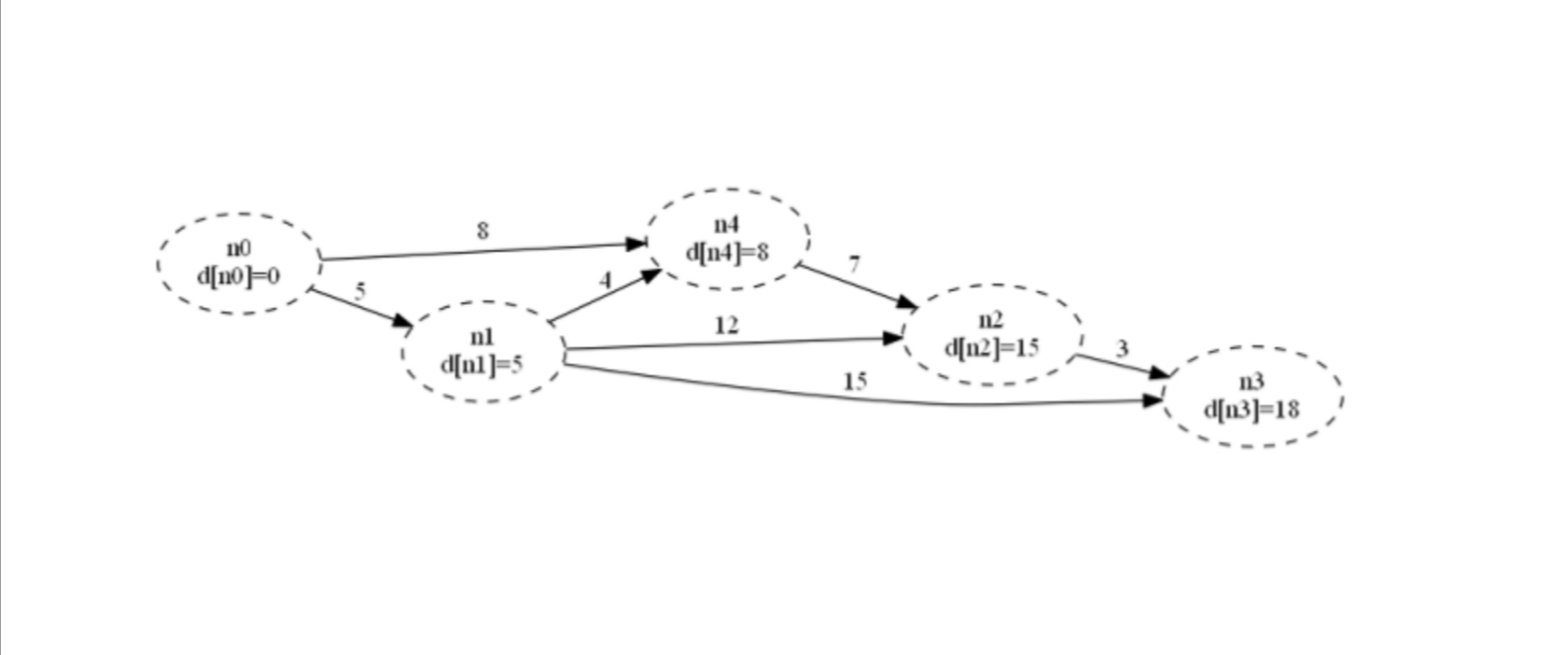
$\color{red}{注：这个算法的使用前提是不能有负权边}$。

• 时间复杂度，朴素方式 $O(V^2)$
• 优先队列优化，$O(V\log V)$

模版题

Heat Wave G

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using std::vector;

const int N = 2505;

int n, m, s, t;
int d[N];
int vis[N]; // 记录每个点有没有在S集合中 

struct Edge {
    int v, w;

    Edge(int v, int w) : v(v), w(w) {}
};

vector<Edge> adj[N];

// 用于装优先队列里的每一个元素
struct Node {
    int u, d;

    Node(int u, int d) : u(u), d(d) {}

    bool operator< (const Node& a) const {
        return d > a.d; // 令d大的反而小 
    }
}; 

void dijkstra() {
    std::memset(d, 0x3f, sizeof d);
    d[s] = 0;
    std::priority_queue<Node> q;
    q.push(Node(s, 0));
    while (!q.empty()) {
        int u = q.top().u;
        q.pop();
        if (u == t) return;
        if (vis[u]) continue;
        vis[u] = 1; // 将u加入S中 
        for (int i = 0; i < adj[u].size(); ++i) {
            int v = adj[u][i].v;
            int w = adj[u][i].w;
            if (d[v] > d[u] + w) {
                d[v] = d[u] + w;
                q.push(Node(v, d[v]));
            }
        }
    }
} 

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    cin >> n >> m >> s >> t;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        adj[u].push_back(Edge(v, w));
        adj[v].push_back(Edge(u, w));
    }

    dijkstra();

    cout << d[t] << '\n';

    return 0;
}

SPFA

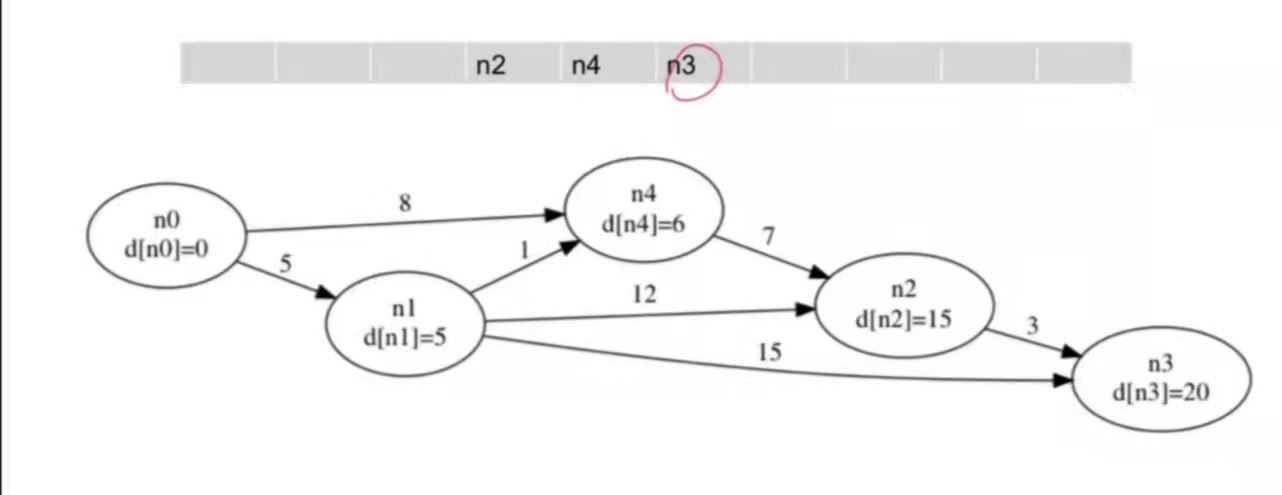
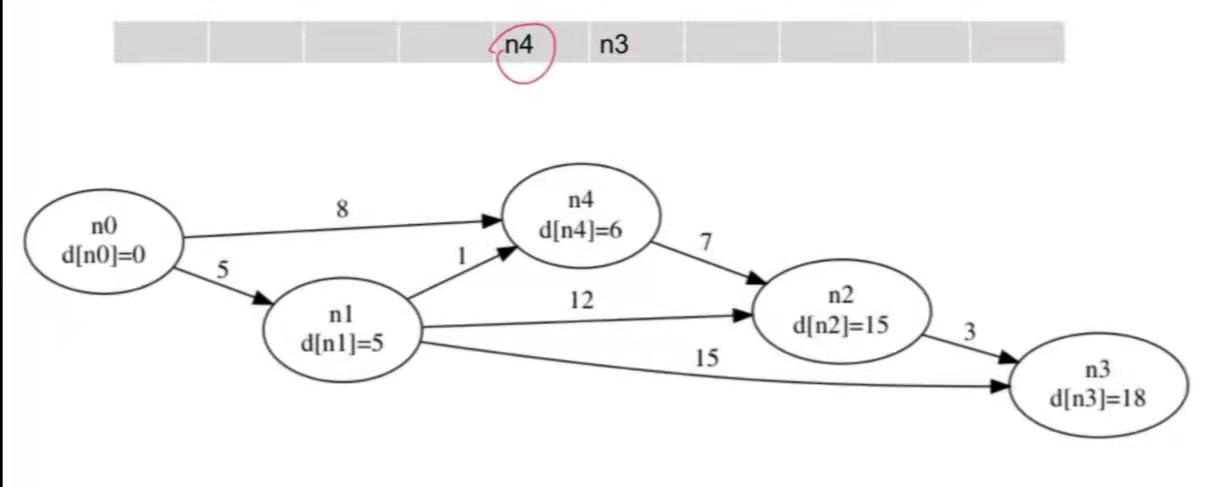
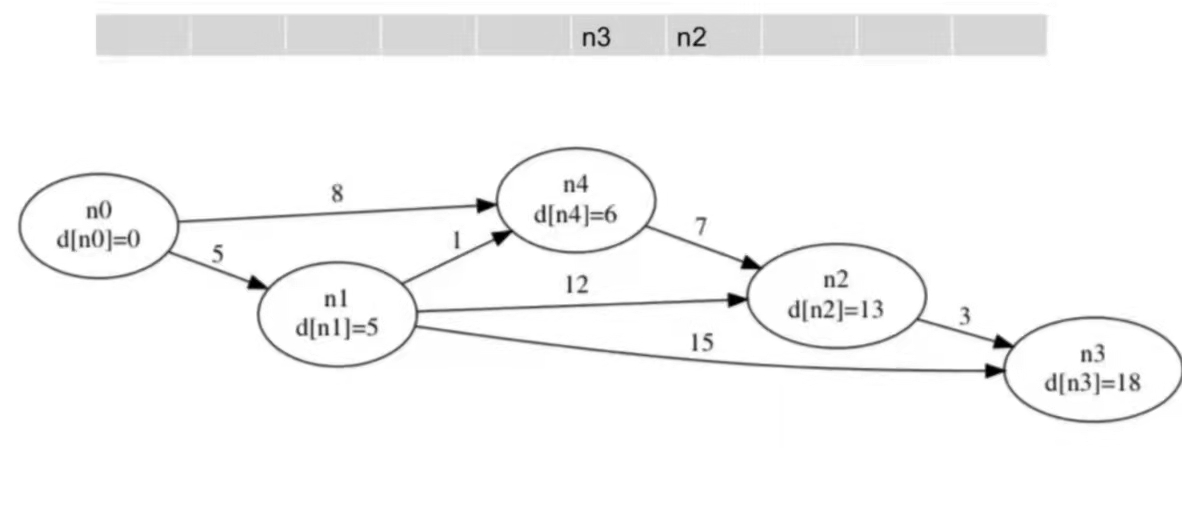
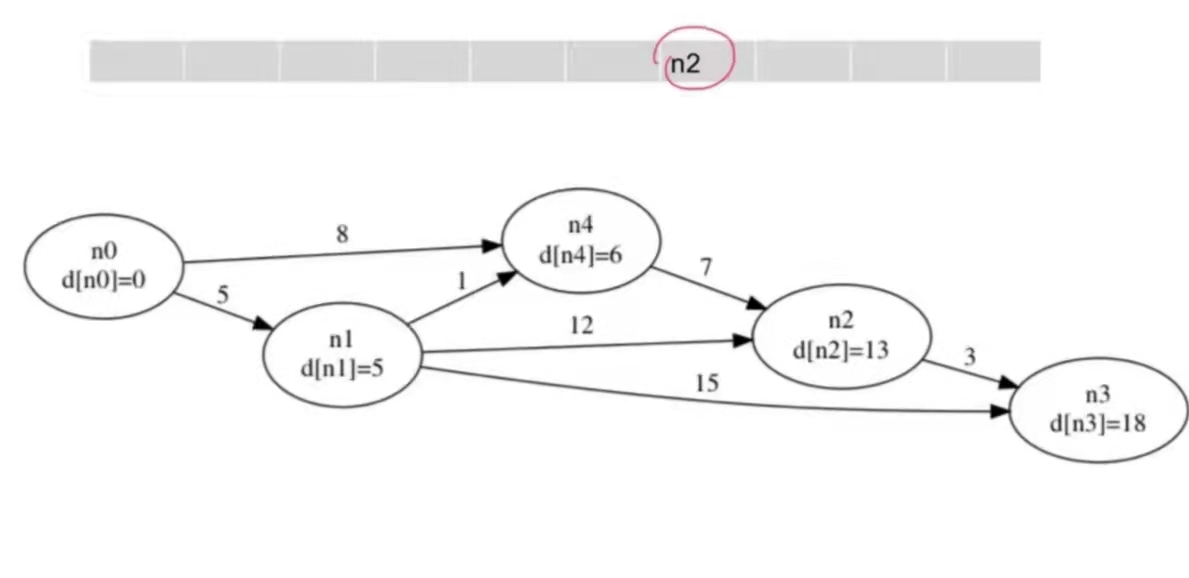
维护一个队列，里面存放所有需要进行更新的点。
初始时队列中只有一个源点 $S(d[S] = 0)$。
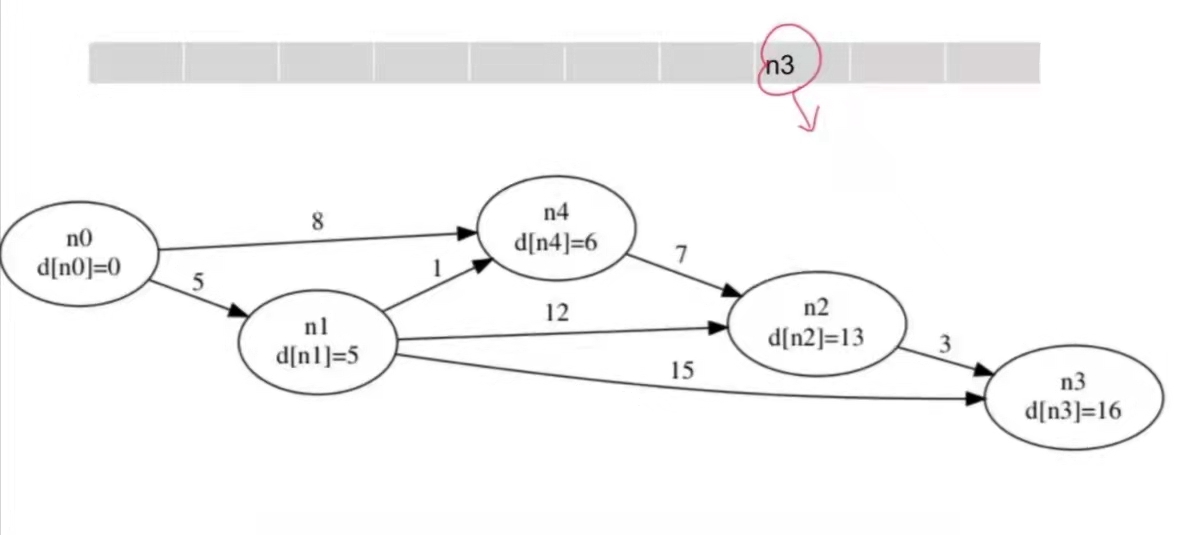
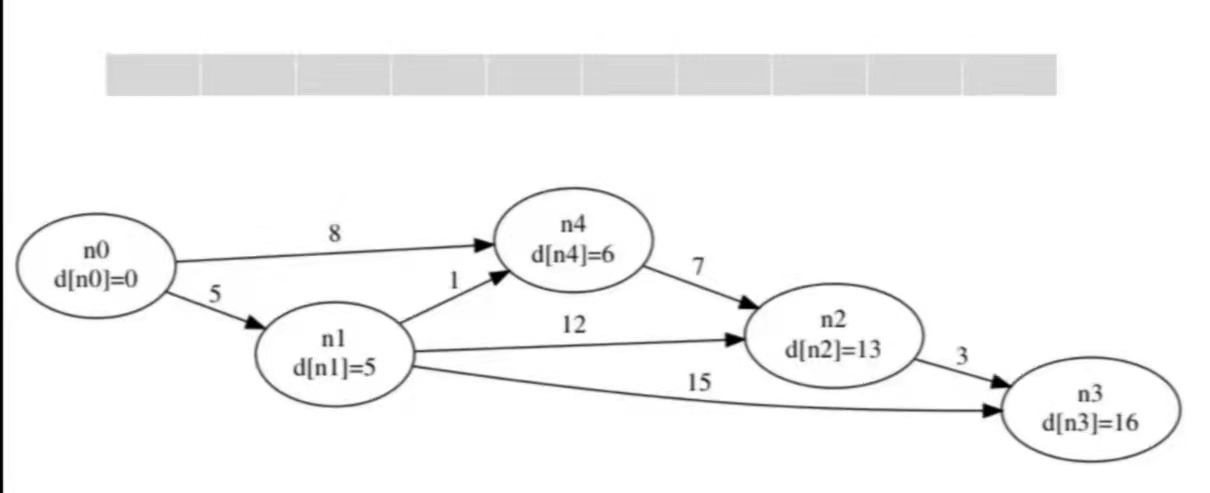
每次取出队头的点 $u$，尝试松弛 $u$ 的所有出边 $<u, v\>$，若能松弛 $(d[u] + w[u][v] < d[v])$，则改进 $d[v]$。此时由于 $s \to v$ 的最短距离 $d[v]$ 变小了，有可能通过 $v$ 可以改进其他结点，将其 push 进队。
这样一直迭代下去直到队列为空，也就是 $d[i]$ 都确定下列，结束算法。
若一个点最短路被改进的次数达到 $V$（结点数），则有负权环。
那么可以用 $spfa$ 算法判断图有负权环。
$spfa$ 算法复杂度的理论上界为 $O(VE)$。在实际情况下表现得非常好，往往能够达到 $O(10E)$。

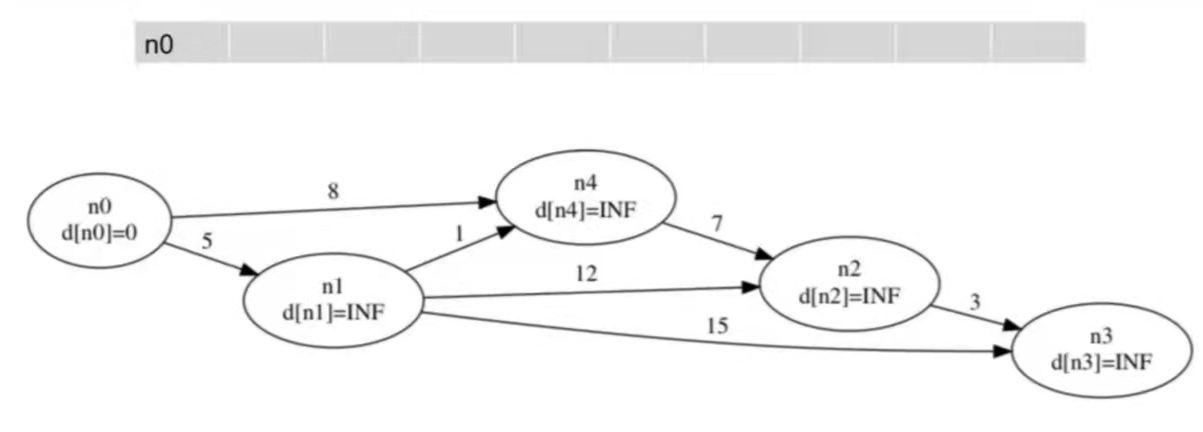
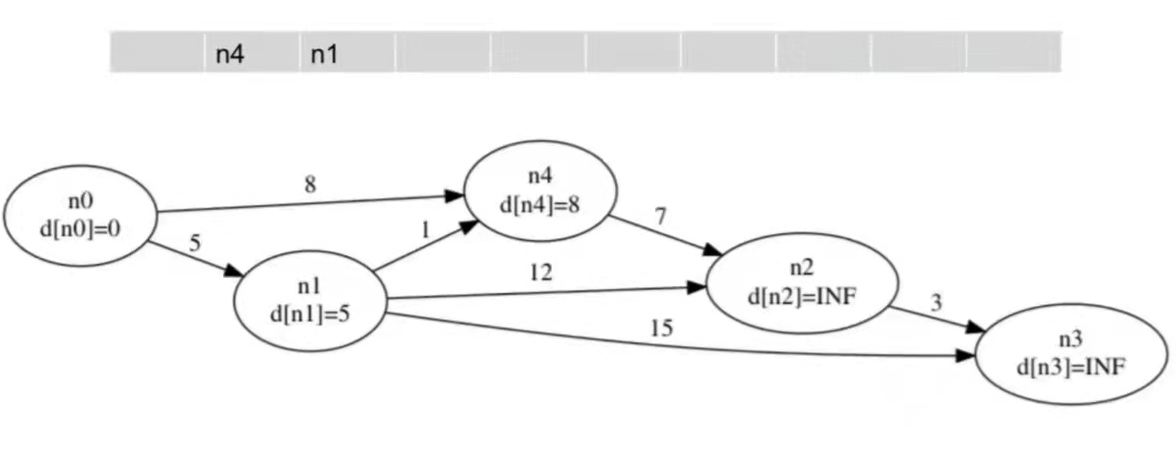
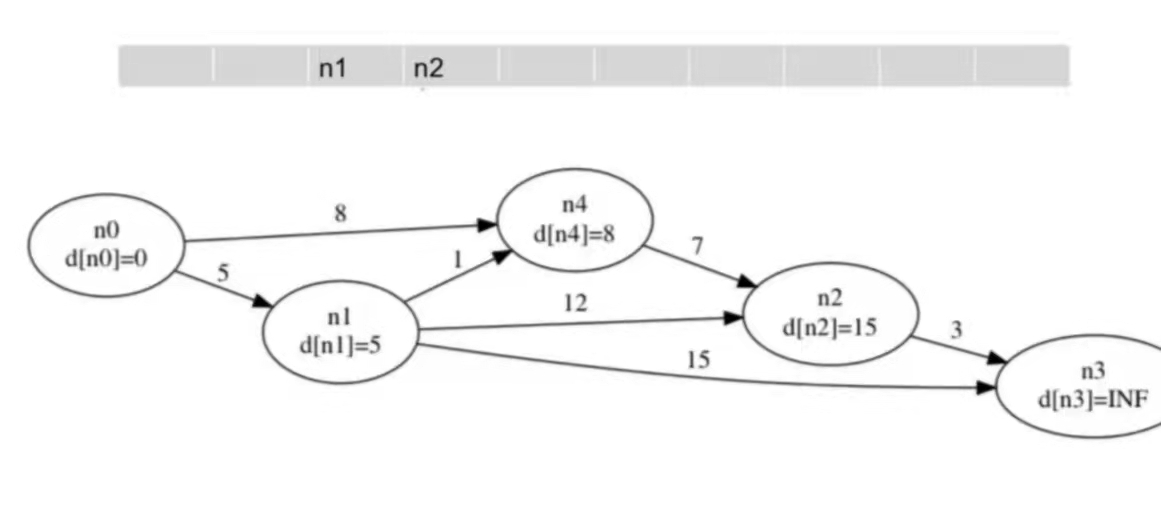
Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::queue;
using P = std::pair<int, int>;

const int MX = 10005;
int n, m, s;
int vis[MX];
int d[MX];
vector<vector<P>> es;

const int INF = (1<<31) - 1;
void spfa() {
    rep(i, n) d[i] = INF;
    queue<int> q;
    q.push(s); vis[s] = 1; d[s] = 0;
    while (q.size()) {
        int u = q.front(); q.pop();
        vis[u] = 0;
        for (auto e : es[u]) {
            int v = e.first;
            int w = e.second;
            if (d[u] + w < d[v]) {
                d[v] = d[u] + w;
                if (vis[v] == 0) {
                    vis[v] = 1;
                    q.push(v);
                }
            }
        }
    }
}

int main() {
    cin >> n >> m >> s;

    es.resize(n + 1);
    rep(i, m) {
        int u, v, w;
        cin >> u >> v >> w;
        es[u].emplace_back(v, w);
    }

    spfa();

    rep(i, n) cout << d[i] << " ";

    return 0;
}

单目标最短路

给定带权有向图 $G$（无自环），求从各个顶点到某一指定顶点 $t$ 的最短路径。

输入格式

第一行三个整数 $n, m, t$，表示图中点的数目，边的数目，以及点 $t$ 的编号
接下来 $m$ 行，每行三个整数 $u, v, w$，表示一条有向边

输出格式

$n$ 个整数，表示每个点到 $t$ 的最短路长度，以空格隔开。如果无法到达 $t$ 点，输出 $-1$

分析：

怎么做呢？难道要调用 $n$ 次单源最短路算法？不用的，只需要把输入中所有的边反过来，建“反向图”在反向图上从 $t$ 出发到所有点的最短路径，就是原图中从所有点到 $t$ 的最短路径。

寻找负权环

给定带权有向图 $G$，图中存在一个负权环（且仅有一个），请输出环上所有点（按编号从小到大的顺序）

输入格式

第一行三个整数 $n, m$，表示点的数目，边的数目
接下来 $m$ 行，每行三个整数 $u, v, w$，表示一条边

输出格式

一行，表示负权环上所有的点

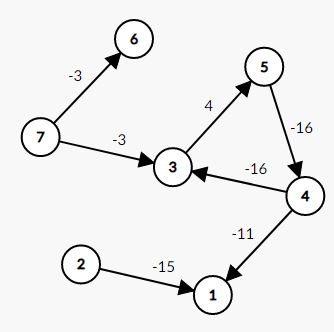
分析

先想办法找到负权环上的任意一个点。
图上的点可以分为 $3$ 类，$1:$ 负权环上的，$2:$ 能走进负环的，$3:$ 走不进负环的
可以在图上每个点为起点，调用一次 $spfa$，对于前两类点，在 $spfa$ 的过程中，一定能找到一个点的最短路被改进了 $n$ 次，则 $spfa$ 函数返回这个点。
对于第三类点进去，$spfa$ 返回 $-1$ 即可。

$spfa$ 函数里面记录每个点被改进的次数，如果达到 $n$ 次，就返回用一个 pre 数组记录每个点的父亲，备用

int spfa(int u) {
    memset(vis, 0, sizeof vis);
    memset(dis, 0x3f, sizeof dis);
    memset(cnt, 0, sizeof cnt); // 记录每个点被改进的次数 
    memset(pre, 0, sizeof pre);
    dis[u] = 0;
    queue<int> q; q.push(u); vis[u] = 1;
    while (q.size()) {
        u = q.front(); q.pop();
        vis[u] = 0;
        for (auto e : es[u]) {
            int v = e.first;
            int w = e.second;
            if (dis[u] + w < dis[v]) {
                dis[v] = dis[u] + w;
                cnt[v]++; pre[v] = u;
                if (cnt[v] == n) return v;
                if (vis[v] == 0) {
                    q.push(v);
                    vis[v] = 1;
                } 
            }
        }
    }
    return -1;
}

• 当找到负权环上的点以后，沿着刚才 pre 数组记录的父亲的方向，往回 $dfs$ 走一遍，用 step 数组记录目前走到第几步了。当走回一个走过的点 $v$ 的时候，从 $v$ 的步开始的这些点都属于负权环，排序输出。
• 走到的每个点走记录在一个 ans 数组里面，用 start 变量记录重合点的步

void dfs(int u, int s) {
    step[u] = s;
    ans.push_back(u);
    int v = pre[u];
    if (ste[v] != -1) {
        start = step[v];
        return;
    }
    dfs(v, s + 1);
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        es[u].emplace_back(v, w); 
    }

    memset(step, -1, sizeof step);

    for (int i = 1; i <= n; ++i) {
        int v = spfa(i);
        if (v != -1) {
            dfs(v, 0);
            break;
        }
    }

    sort(ans.begin(), ans.end());

    for (int i = start; i < ans.size(); ++i) cout << ans[i] << " ";

}

判负环模板

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define rrep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::queue;
using P = std::pair<int, int>;

const int MX = 2005;
int n, m;
int vis[MX];
int dis[MX];
int cnt[MX];
vector<vector<P>> es;

int spfa(int u) {
    memset(vis, 0, sizeof vis);
    memset(dis, 0x3f, sizeof dis);
    memset(cnt, 0, sizeof cnt); // 记录每个点被改进的次数 
    dis[u] = 0;
    queue<int> q; q.push(u); vis[u] = 1;
    while (q.size()) {
        u = q.front(); q.pop();
        vis[u] = 0;
        for (auto e : es[u]) {
            int v = e.first;
            int w = e.second;
            if (dis[u] + w < dis[v]) {
                dis[v] = dis[u] + w;
                cnt[v]++; 
                if (cnt[v] == n) return v;
                if (vis[v] == 0) {
                    q.push(v);
                    vis[v] = 1;
                } 
            }
        }
    }
    return -1;
}

int main() {
    int t;
    cin >> t;

    while (t--) {
        cin >> n >> m;
        es.clear();
        es.resize(n + 1);
        rep(i, m) {
            int u, v, w;
            cin >> u >> v >> w;
            es[u].emplace_back(v, w); 
            if (w >= 0) es[v].emplace_back(u, w); 
        }
        bool ok = spfa(1) != -1;
        cout << (ok ? "YES\n" : "NO\n");
    }

    return 0;
}

次短路

例题： [USACO06NOV]Roadblocks G

给定一个 $n$ 个点 $r$ 条边的无向图，求从点 $1$ 到点 $n$ 的严格次短路（即长度大于最短路径的路径中最短的一条，一条边可以经过多次）。

限制：

• $1 \leqslant n \leqslant 5 \times 10^3$
• $1 \leqslant r \leqslant 10^5$
• $1 \leqslant w \leqslant 5 \times 10^3$

分析：

在任何时刻，如果发现了一条新的从 $1$ 到 $i$ 的路径，则该路径存在以下情况：

1. 该路径长度小于目前的 $1$ 到 $i$ 的最短路。此时的处理方式是将目前的次短路用目前的最短路替换，而最短路替换为新路径。
2. 该路径长度等于目前的最短路，直接舍去。
3. 该路径长度大于目前的最短路且小于目前的次短路。此时的处理方式是直接用这条路径替换目前的次短路径。
4. 该路径长度大于或等于目前的次短路，直接舍去。

对于本题而言，长度大于目前已知路径中的次短路的路径都是没有意义的，因此，只需考虑当前状态下的最短路和次短路即可。

维护两个数组 dist1 和 dist2，分别代表从起点走过来的最短路和次短路的长度
跑 $\rm{spfa}$，从队列里拿出来 $u$ 点，发现一条边从 $u$ 到 $v$
此时，从 $\rm{dist1}[u]$，有可能可以更新 $\rm{dist1}[v]$，也可能更新 $\rm{dist2}[v]$
从 $\rm{dist2}[u]$ 可能更新 $\rm{dist2}[v]$

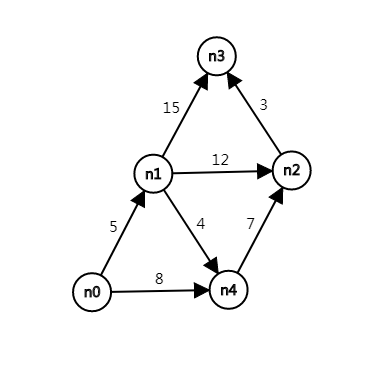
注意，严格次短路问题看起来不能用 $\rm{Dijkstra}$ 算法，当从优先队列拿出来点 $u$ 的时候，不能保证 $u$ 点的次短路也是最短的，所以 $u$ 点有可能需要重复进优先队列。可以结合下图思考一下：

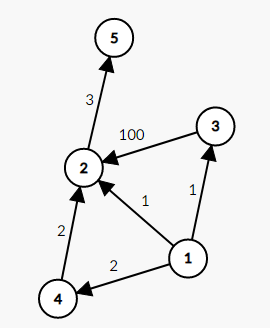
$2$ 号店如果从优先队列出队，一会儿 $1 \to 4 \to 2$ 这条路径会让它重复进队

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::queue;
using P = std::pair<int, int>;

const int MX = 100005;
int n, m;
int vis[MX];
int d1[MX];
int d2[MX];
vector<vector<P>> es;

void spfa() {
    memset(d1, 0x3f, sizeof d1);
    memset(d2, 0x3f, sizeof d2);
    queue<int> q;
    q.push(1); vis[1] = 1; d1[1] = 0;
    while (q.size()) {
        int u = q.front(); q.pop();
        vis[u] = 0;
        for (auto [v, w] : es[u]) {
            bool isPush = false;
            if (d1[u] + w < d1[v]) {
                d2[v] = d1[v];
                d1[v] = d1[u] + w;
                isPush = true;
            }
            if (d1[u] + w > d1[v] and d1[u] + w < d2[v]) {
                d2[v] = d1[u] + w;
                isPush = true;
            }
            if (d2[u] + w > d1[v] and d2[u] + w < d2[v]) {
                d2[v] = d2[u] + w;
                isPush = true;
            }
            if (isPush and !vis[v]) {
                vis[v] = 1;
                q.push(v);
            }
        }
    }
}

int main() {
    cin >> n >> m;

    es.resize(n + 1);
    rep(i, m) {
        int u, v, w;
        cin >> u >> v >> w;
        es[u].emplace_back(v, w);
        es[v].emplace_back(u, w);
    }

    spfa();

    cout << d2[n] << '\n';

    return 0;
}

$\rm{Dijkstra}$ 算法真的不行么？

能不能类似一个点拆两个点的思路，给每个点两次出优先队列的机会？当它最短路最短的时候，当它次短路最短的时候，都可以让它出队然后更新别人，这时候它不会重复进队了。

Code:

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using std::priority_queue;
using P = std::pair<int, int>;

const int MX = 100005;
int n, m;
int vis[MX][2];
int d[MX][2];
vector<vector<P>> es;

struct Node {
    int u, d, idx; // idx: 0: 因最短路被改小而进队 1：因次短路被改小而进队
    Node(int u, int d, int idx): u(u), d(d), idx(idx) {}
    bool operator<(const Node &other) const {
        return d > other.d;
    }
};

void Dijkstra() {
    memset(d, 0x3f, sizeof d);
    d[1][0] = 0;
    priority_queue<Node> q;
    q.push(Node(1, 0, 0));
    while (q.size()) {
        Node t = q.top(); q.pop();
        int u = t.u;
        int idx = t.idx;
        if (vis[u][idx]) continue;
        vis[u][idx] = 1;
        for (auto [v, w] : es[u]) {
            if (d[u][0] + w < d[v][0]) {
                d[v][1] = d[v][0];
                d[v][0] = d[u][0] + w;
                q.push(Node(v, d[v][0], 0));
                q.push(Node(v, d[v][1], 1));
            }
            else if (d[u][0] + w > d[v][0] and d[u][0] + w < d[v][1]) {
                d[v][1] = d[u][0] + w;
                q.push(Node(v, d[v][1], 1));
            }
            else if (d[u][1] + w > d[v][0] and d[u][1] + w < d[v][1]) {
                d[v][1] = d[u][1] + w;
                q.push(Node(v, d[v][1], 1));
            }
        }
    }
}

int main() {
    cin >> n >> m;

    es.resize(n + 1);
    rep(i, m) {
        int u, v, w;
        cin >> u >> v >> w;
        es[u].emplace_back(v, w);
        es[v].emplace_back(u, w);
    }

    Dijkstra();

    cout << d[n][1] << '\n';

    return 0;
}

一些练习题

1. Train
2. 最短路计数
3. 基础最短路练习题