描述

在网络中关键节点的判断将成为影响网络连通性的主要因素。节点之间通过关键节点传递信息，如在我们以太网中的网关。当网关节点失效，那么两个网络之间的节点就不能够进行通信。在无线传感器网络中，会造成不能及时监控部分区域的信息。这次请编写程序主要实现一个简单的判断关键节点方法。

关键节点的定义：在图中有那么一些特殊的节点，如果去除这些点，则会使得从某个初始节点到某个终止节点的这两个节点变得不连通。这些点被称为最短路径上的关键点。现举例说明如下：

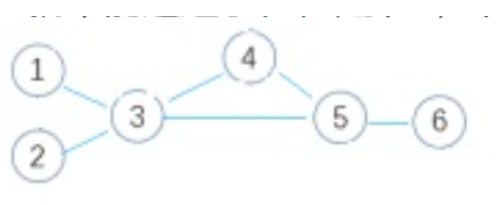
如图所示，若网络结构由6个节点组成，从节点1到节点6之间是连通的，并且有两个关键节点3和5。也就是说，如果这两个节点任何一个失效了，1到6就不能连通了。但是节2，节点4失效，不会影响1到6的连通。

现给定一个无权图，以及起始节点和终止节点，要求输出该图上，这对节点间的关键点数目。

输入

多组数据测试，每组测试数据如下：
输入多行：
第1行：输入节点数N（N<=1000）的路径数roat（N(N-1)/2<=roat<=3N）
第2行：第2+roat-1行： 输入每一节路径的起点与终点
第2+roat行：输入需查验的起点与终点
输出一行：
关键节点数

输出

每组输出一行：
关键节点数

样例输入

6 6   
1 3    
2 3    
3 4    
3 5   
4 5    
5 6   
1 6    

样例输出

2

思路

用并查集的数据结构解决
遍历所有节点（for (int i = 1; i <= n; i++)）

重置并查集状态：考虑每个节点i时，重置并查集转态，考虑，以便独立测试节点i是否是关键节点
构建不包含当前节点的图：遍历所有边，若边的两个端点都包含节点i，则将两个端点合并到一个集合
检查连通性：移除节点i后，检查起点x和起点y是否连通（即看find(pre)是否相等），若不连通，说明节点i时关键节点

code

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
typedef pair<int, int> PII;
int pre[maxn];
void init() {
    for (int i = 1; i < maxn; i++) {
        pre[i] = i;
    }
}
int find(int x) {
    return pre[x] == x ? x : pre[x] = find(pre[x]);
}
void merge(int x, int y) {
    int rootx = find(x);
    int rooty = find(y);
    if (rootx != rooty) {
        pre[rootx] = rooty;
    }
}
int main()
{
    int n, m;
    while (cin >> n >> m) {//操作数
        vector<PII> road;
        for (int i = 0; i < m; i++) {
            int a, b;
            cin >> a >> b;
            road.push_back({ a,b });
        }
        int x, y;//查验起点、终点
        cin >> x >> y;
        int ans = 0;//关键点个数
        for (int i = 1; i <= n; i++) {
            if (i == x || i == y) continue;//起始点和终点不是关键节点 
            init(); 
            for (int j = 0; j < m; j++) {//遍历所有的边 
                PII temp = road[j];//获取第j条边的起点、终点 
                if (temp.first != i && temp.second != i) {
                //若j条边的起点、终点都不是当前节点i,则这条边就不会被当前节点阻断 
                    merge(temp.first, temp.second);
        //将边的起点和终点合并至一个集合中,模拟这条边连接作用 
                }
            }
            if (find(x) != find(y)) ans++;
            //在排除节点i后,检查x和y是否联通,若不联通,说明节点i为一个关键节点 
        }
        cout << ans << endl;
    }
    return 0;
}