堆 (Heap)

1. 定义 : 堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。 故通常我们用完全二叉树来维护一个一维数组

2. 分类 : 按照堆的特点可以把堆分为大顶堆和小顶堆

----------大顶堆：每个结点的值都大于或等于其左右孩子结点的值

----------小顶堆：每个结点的值都小于或等于其左右孩子结点的值

3. 完全二叉树维护的一维数组的特点

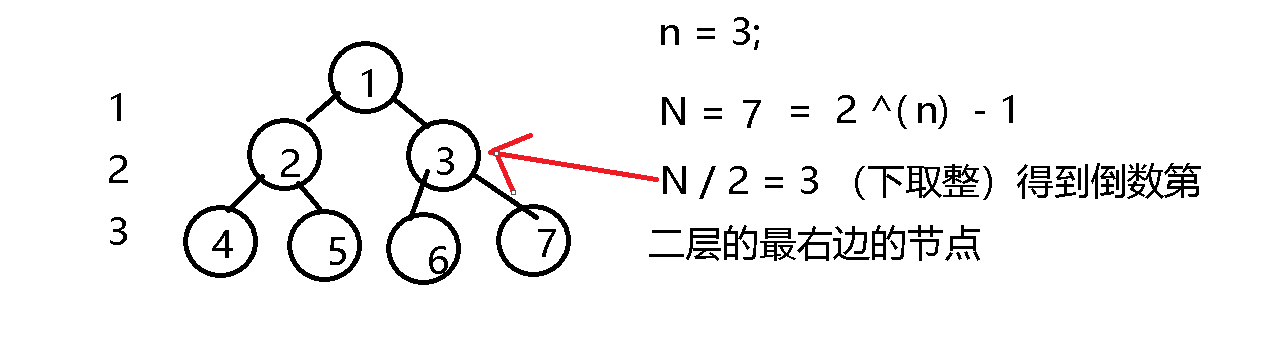
再开始具体讲解堆之前，我们先来了解一下完全二叉树的特点，及其用它来维护的一维数据有什么特点，首先完全二叉树的特点就是除了最后一层外，单看 1 ~ n - 1层这就是一颗满二叉树.对于满二叉树, 如果有n层，那么其节点数为 2 ^ n - 1; 其中第k层的节点数为2 ^ (k - 1). 若将节点的总数 N / 2 即 得到 2 ^ (n - 1) - 1;这里的结果进行了下取整， 这个为倒数第二层的最右边的那个节点。对于完全二叉树来说， N / 2得到的是最后一个非叶子节点的序号，具体推导 ：

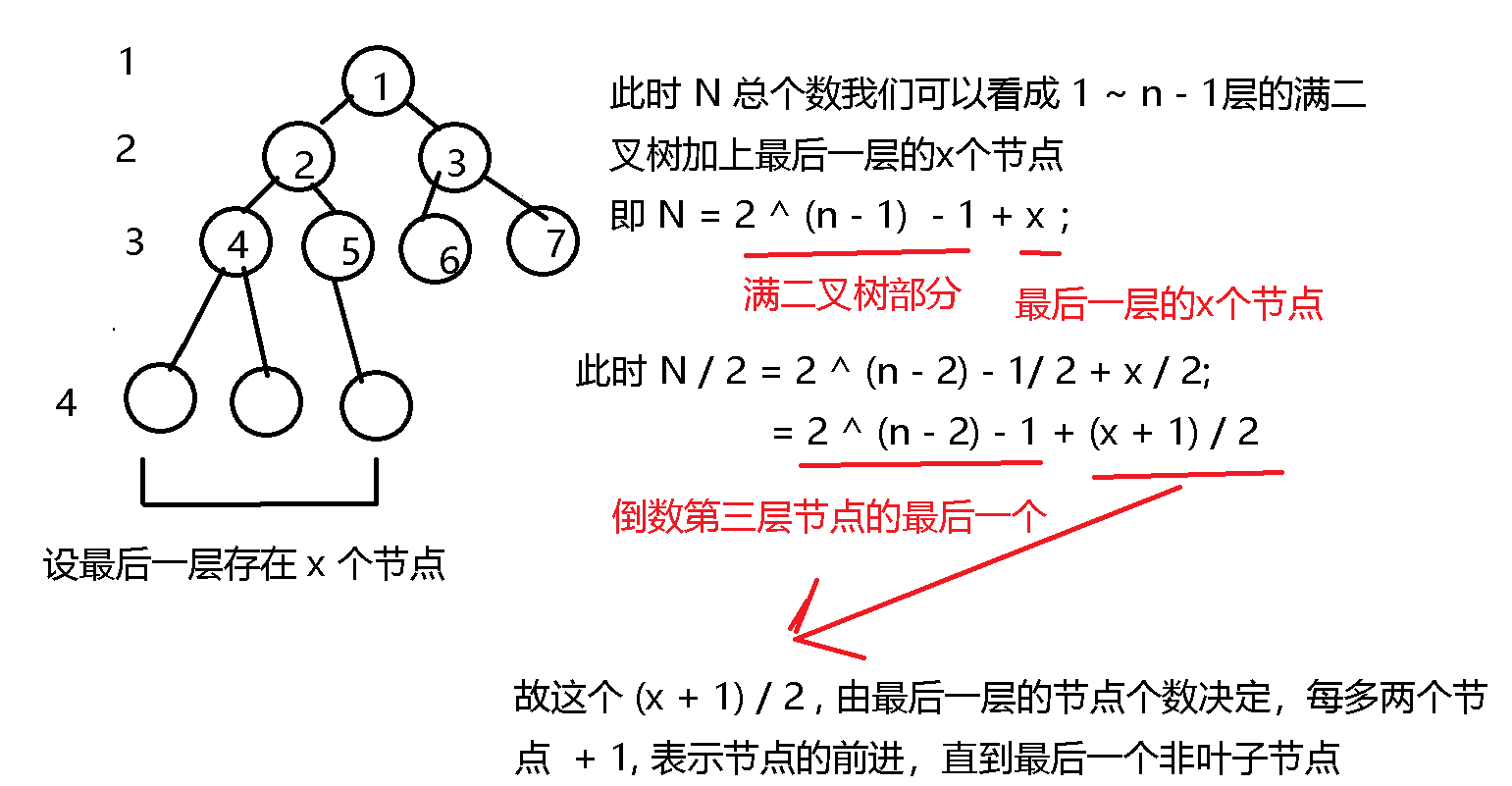
在完全二叉树中我们发现关系就是 如果父节点的序号为 x, 那么其左孩子节点若存在其序号为 2 * x, 右孩子存在则其序号为 2 * x + 1; 那么一个节点的父节点则为 x / 2; 故根据这个序号特点，我们将序号作为数组的下标，将一颗完全二叉树用一个一维数组存储。

4. 堆的基本操作

由于堆是一个完全二叉树, 且其每个结点的值都小于或等于其左右孩子结点的值(这里以小顶堆为例子).故我们需要一些操作使得我们除了叶子节点之外都满足结点的值都小于或等于其左右孩子结点的值，故为了实现这个我们对于节点有两个基本的操作，上浮up和下沉down.

#include<iostream>
using namespace std;

constexpr int N = 1e+5 + 10;
int n,m,h[N], s;         

// h[N] 一维数组用于存储完全二叉树上的节点的值，其下标判断各个节点之间的关系
// 例如 h[x] 的 左孩子节点的值为 h[2 * x] . 右孩子节点的值为 h[2 * x + 1], 其父节点为 h[x / 2];  
// 假定都存在, 2 * x <= 节点总数 2 * x + 1 <= 节点总数， 父节点 x / 2 >= 1
// s 用来表示当前堆中的节点的总数

1.下沉操作down
对于一个节点，我们判断其节点值与左右节点的值相比较，如果当前节点的值不满足都小于或等于其左右孩子结点的值， 那么我们将节点与左右节点中较小的那个进行交换操作，由于进行了交换，故当前这棵子树中满足了小顶堆的特点，但由于交换了位置，故需要判断被交换位置后的子树位置此时的节点与其新左右孩子的节点值是否满足小顶堆，故这里我们就需要递归.

// 代码down操作实现
auto down(int x) -> int
{
    int t = x;
    if(2 * x <= n && h[t] > h[2 * x]) t = 2 * x;    // 与左孩子节点值比较
    if(2 * x + 1 <= n && h[t] > h[2 * x + 1]) t = 2 * x + 1;  // 与右孩子节点值比较
    if(t != x) swap(h[t], h[x]), down(t);   // 若t != x，说明此时节点并不不符合堆，故与其中较小的孩子进行交互
    // 交换完后，此时被交互到孩子位置的节点与其新左右孩子的节点值是否满足小顶堆，故这里我们就需要递归.
}

2.上浮操作up
对于一个节点我们与其父节点进行比较，如果当前的父节点比其节点值大，则不满足小顶堆的条件，故此时这两个节点需要进行交互，交换完毕后的成为新的父节点，此时由于位置变动，其需要继续与原本父节点的父节点进行比较，直到都满足堆条件为止，同样这里可以用递归或者while循环来实现。

// 代码up操作的实现
auto up(int x) -> void
{
    while(x / 2 && h[x / 2] > h[x])  // 若此时父节点存在，且父节点值大于自己，不满足条件需要进行交换
    {
        swap(h[x / 2] , h[x]);
        x /= 2;
    }
}

3.由down操作和up操作完成堆中数据的操作
对于堆的数据进行操作，均可由这两种基本操作组合来完成
(1) 插入一个数 : 即增加一个叶子节点，由于其没有孩子，故只能上浮操作，来将这个新插入的值调整到合适的位置，使得整个堆都符合小顶堆的条件。 增加一个叶子节点的操作为h[++s] = x; 然后再进行上浮 up(s); s为当前堆中节点的总数

(2) 找出堆中数据的最小值，根据小顶堆的特点我们知道，其根节点即为最值点，故h[1];(下标从1开始) 即为要找的答案，对于大顶堆来说，这个就是最大值了。

(3) 删除一个元素: 此时我们只需让需要删除的元素与最后一个叶子节点进行交换，交换后我们进行上浮和下沉， 由于这两种操作只有其中一种会被执行，故我们在代码实现的时候并不需要在这里作判断执行哪一个，直接写两个就ok了，反正只会执行满足条件的那一个. 故其代码实现为

// 设要交换的位置为 x 
    swap(h[x], h[s]); // 交换要删除的元素和最后一个叶子节点的位置
    --s; // 表示删除了一个元素，因为如果对于堆，直接删堆中元素操作复杂，但在一维数组中直接删除最后一个元素很方便
    down(x), up(x); //执行其中一个操作，具体的操作由此时被交换叶子节点的值与新父子节点和孩子节点值的关系决定

    // 如果是删除堆顶元素
    swap(h[1], h[s--]);
    down(1);                 // 此时只有下沉操作

(4) 修改其中一个元素的值 ： 直接修改其位置上的值，然后由于其节点值发生了改变，故需要判断此时堆是否满足条件，故进行上浮和下沉，当然两种操作只会执行其中的一种.

5.例题分析

练习链接 : 模拟堆

思路分析

这道例题的一个难点在于需要保存额外的信息，即需要保存每个下标对于的是第几个插入的数
这里我们额外用到了两个数组 hp 数组 和 ph数组

hp[i] = k, 含义为下标为i的元素其为第k个元素插入

ph[i] = k, 含义为第i个插入的元素其下标为k

故这里的交换的话，就不能仅仅是简单对应节点的值进行交互，还要将其下标与第几个数插入对应的关系也跟着一起交互，故这里自带的swap函数显然不够用，故这里我们自己实现了h_swap函数，注意这个函数的参数是用数组的下标.

#include<iostream>
#include<string>
using namespace std;

constexpr int N = 1e+5 + 10;
int m, s, cnt, h[N], hp[N], ph[N];

auto h_swap(int x, int y) -> void
{
    swap(ph[hp[x]], ph[hp[y]]);  // ph数组存储的为值第几个插入对应的下标
    swap(hp[x], hp[y]);          // hp数组存储的是第几个插入的信息的信息
    swap(h[x], h[y]);            // 交互两个节点的值
}

auto down(int x) -> void
{
    int t = x;
    if(2 * x <= s && h[t] > h[2 * x]) t = 2 * x;
    if(2 * x + 1 <= s && h[t] > h[2 * x + 1]) t = 2 * x + 1;
    if(t != x) h_swap(t, x), down(t);
}

auto up(int x) -> void
{
    while(x / 2 && h[x / 2] > h[x])
    {
        h_swap(x / 2 , x);
        x /= 2;
    }
}

auto main() -> int
{
    cin >> m;
    while(m--)
    {
        string op; cin >> op;      // 根据op的值执行不同的操作，这些操作前面都讲过了
        if("I" == op) 
        {
            int a; cin >> a;
            h[++s] = a;
            ++cnt;
            hp[s] = cnt, ph[cnt] = s;
            up(s);
        }
        else if("PM" == op) cout << h[1] << endl;
        else if("DM" == op)
        {
            h_swap(1, s); --s;
            down(1);
        }
        else if("D" == op)
        {
            int k; cin >> k;
            int idx = ph[k]; h_swap(idx, s); --s;
            down(idx), up(idx);
        }
        else 
        {
            int k, x; cin >> k >> x;
            int idx = ph[k]; h[idx] = x;
            down(idx), up(idx);
        }
    }
    return 0;
}