定义

对于一个有向图 $G$ 来说，它有一个起点 $S$，若 $x,y$ 满足从 $S$ 到 $y$ 的所有路径都经过 $x$，那么称 $x$ 为 $y$ 的其中一个支配点，特殊地，$y$ 本身和 $S$ 都是 $y$ 的支配点。

设 $X_p$ 表示点 $p$ 的支配点组成的集合，定义点 $p$ 的最近支配点 $u$，当且仅当其满足 $X_p = X_u \cup \{p\}$。

可以证明 $p$ 一定存在唯一的最近支配点：

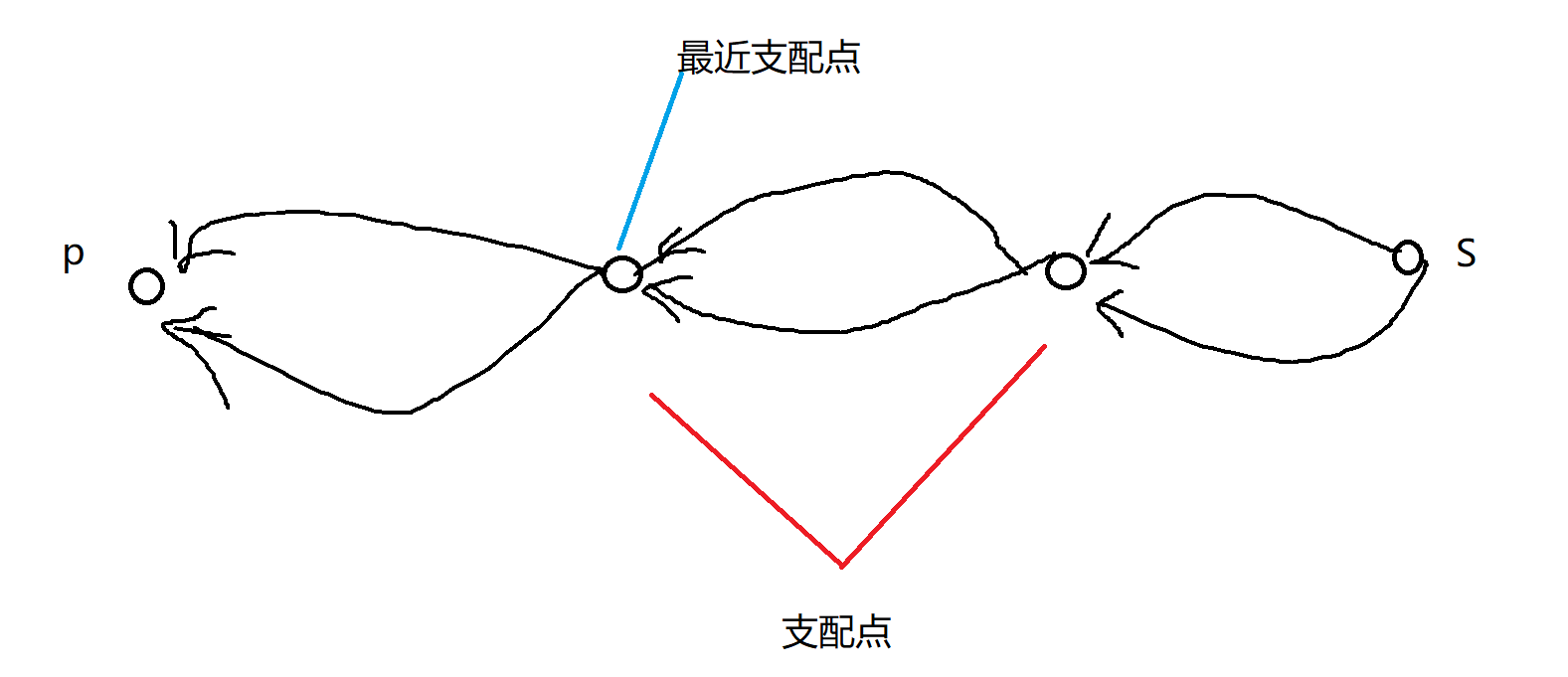
我们对与每一个点 $p$，从它的最近支配点向它两一条边，于是得到了一颗树，这就是支配树。

DAG 求支配树

[ZJOI2012] 灾难

给定一颗有向无环图，对于每一个点 $u$，求 $\sum_{i=1}^n [u \in X_i]$。
$1\leq n\leq 65534$，$1\leq m\leq 3\times 10^5$

• 进行拓扑排序；
• 排序过程中更新 $fa_j$ 的值，设当前点为 $u$，更新节点 $j$，若 $fa_j$
  等于 $0$，则 $fa_j = u$，否则 $fa_j = lca(j, u)$，$lca$ 求的是目前支配树上的，用倍增求，当 $fa$ 被修改时，倍增数组也要被修改；
• 支配树为将所有 $fa_u$ 连向 $u$ 后得到的树。

#include <bits/stdc++.h>
using namespace std;

const int N = 70010, M = 4000010;
int n, d[N], fa[N][24], dep[N], siz[N];
int h[N], hh[N], e[M], ne[M], idx;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void add2(int a, int b) {
    e[idx] = b, ne[idx] = hh[a], hh[a] = idx ++ ;
}

void update(int j) {
    for (int i = 1; i < 20; i ++ ) fa[j][i] = fa[fa[j][i - 1]][i - 1];
}

int lca(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    for (int i = 19; i >= 0; i -- )
        if (dep[fa[x][i]] >= dep[y])
            x = fa[x][i];
    if (x == y) return x;
    for (int i = 19; i >= 0; i -- )
        if (fa[x][i] != fa[y][i])
            x = fa[x][i], y = fa[y][i];
    return fa[x][0];
}

void toposort() {
    queue<int> q;
    for (int i = 1; i <= n; i ++ )
        if (d[i] == 0)
            q.push(i), fa[i][0] = n + 1, dep[i] = 1;
    while (q.size()) {
        int t = q.front();
        add2(fa[t][0], t);
        q.pop();
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (fa[j][0]) fa[j][0] = lca(j, t);
            else fa[j][0] = t;
            dep[j] = dep[fa[j][0]] + 1;
            update(j);
            if (-- d[j] == 0) q.push(j);
        }
    }
}

void dfs(int u, int fa) {
    siz[u] = 1;
    for (int i = hh[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        dfs(j, u);
        siz[u] += siz[j];
    }
}

int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    memset(hh, -1, sizeof hh);
    for (int i = 1; i <= n; i ++ ) {
        int x;
        while (scanf("%d", &x), x) {
            add(x, i);
            d[i] ++ ;
        }
    }
    toposort();
    dfs(n + 1, 0);
    for (int i = 1; i <= n; i ++ )
        printf("%d\n", siz[i] - 1);
    return 0;
}

有向图求支配树

还没学。