NO.1 什么是二分法?
NO.2 如何优雅的处理边界条件?
NO.3 二分法一定要有序才能使用吗?
NO.4 证明二分法的时间复杂度
NO.5 一些题目
NO.1 什么是二分法?
二分法(Bisection method),即一分为二的的方法。
对于在区间[a,b]上连续不断且满足f(a)*f(b)<0的函数y=f(x)
通过不断地把函数f(x)的零点所在区间二等分
使区间两个端点逐步逼近零点,进而得到零点的近似值的方法。
说人话:把答案所在的区间逐渐缩小,直到区间内只有答案。
比如猜数字游戏:给定一个1–100之间的正整数,让你猜。猜的过程中给出大小判断的提醒,问怎么才能快速地猜出来?
最快的方法是:每次猜区间的中间点的数字。
如果中间点大于给定数字,下次就猜前半部分的中间点数字;
如果中间点数字小于给定数字,下次就猜后半部分的中间点数字。
例如:给定56。
第一次猜1到100中心的数字:(1+100)/2 = 50,小于给定数字。
第二次猜51到100中心的数字:(51+100)/2 = 75,大于给定数字。
第三次猜51到74中心的数字:(51+74)/2 = 62,大于给定数字。
第四次猜51到62中心的数字:(51+62)/2 = 56。等于给定数字。
结束。
代码
int main() {
int l = 1, r = 100;//l表示猜数区间的左端点,r表示猜数区间的右端点
int target = 56;//给定的数字
while (l < r)
{
int mid = (l + r) / 2;//计算中间点mid的值
if (mid > target)//中间点的值大于给定数字,往左半部分往左部分猜
r = mid - 1;//mid 及 mid右侧数字都大于targ,所以r = mid - 1
else if (mid == target) //mid等于给定数字
{
cout << "猜到了,给定数字是:" << mid;
break;
}
else
l = mid + 1;//中间点的值小于于给定数字,往右半部分往左部分猜
}
}
NO.2 如何优雅的处理边界条件?
2.1 左边界、右边界的更新
先看一个例子:给定一个排好序的整数数组a,数组中可能存在重复元素。给定数组中的一个值target,求出它最后出现的位置。
例如数组a为:[1 3 3 3 5],目标值target = 3。a中最后一个等于3的元素为:a[3],所以结果为3。
最容易想到的解决方法是遍历数组,找出target最后出现的位置即可。时间复杂度是O(n)。
考虑使用二分法:用l指向区间的左端点,r指向区间的右端点,取mid = (l + r) / 2,mid 指向区间中间位置。
左右端点更新规则如下:
如果a[mid] > target,target最后一次出现的位置一定在a[mid]之前,更新r:r = mid - 1。
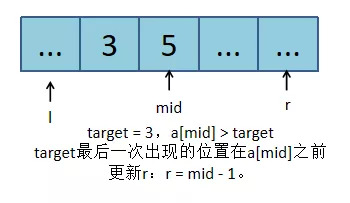
如果a[mid] <= target,target最后一次出现的位置可能在mid处,也可能在a[mid]之后,更新l:l = mid。
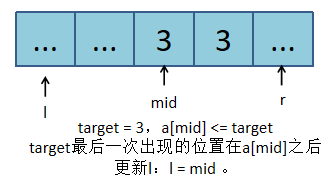
直到 l = r时,区间内只有一个元素,位置l就是target最后一次出现的位置。
看起来很正确的方法,手动模拟下:
第一次:l = 0, r = 4, mid = (l + r) / 2 = 2。a[mid] = 3。符合更新规则2,l更新为mid:l = 2。
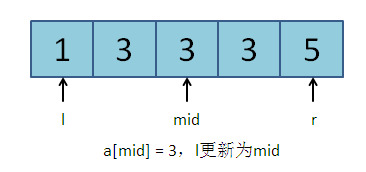
第二次:l = 2, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符合更新规则2,l更新为mid:l = 3。
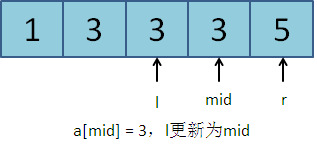
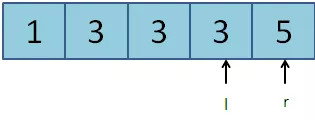
第三次:l = 3, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符合更新规则2,l更新为mid:l = 3。
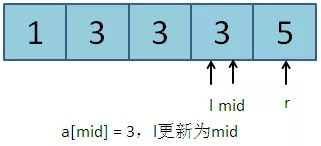
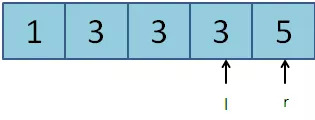
第四次:l = 3, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符合更新规则2,l更新为mid:l = 3。


....
我们发现,从第三次开始陷入了死循环。
来看看为什么出现了这种情况
在第三次处理过程中,l = 3, r = 4。mid = (l + r) / 2 = 3。a[mid] = 3。l更新为mid:l = 3。
可以发现,l更新前的值为3,更新后,l的值还为3。更新前后l的值没变,因此陷入了死循环。
原因在于:通过(l + r) / 2 计算mid的值,结果是向下取整的。
在区间内只有两个元素的时,r的值可以用l + 1代替,因此mid = (l + r) / 2 = (l + l + 1) / 2 = l。
这个时候更新l = mid,l的值更新后依旧为l。下次处理的区间和这次相同,陷入了死循环。
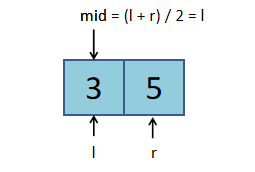
整数除法结果是向下取整,所以用l= mid更新l后,l的值可能等于更新前值,因此陷入死循环。
如何解决l = mid 陷入死循环的问题
改变mid的计算方法,使mid的值只会大于l,这样用l = mid更新l,区间就能不断缩小,就不会陷入死循环。
具体的:让mid的取值为(l + r) / 2向上取整,这样l更新为mid后,l的值一定会大于更新前的值。
(l + r) / 2向上取整的值如何得到
如果l + r为奇数,(l + r) / 2向上取整等于(l + r + 1) / 2向下取整;
如果l + r为偶数,(l + r) / 2向上取整也等于(l + r + 1) / 2向下取整。
因此,只要程序中有l = mid这种情况,mid就用mid = (l + r + 1) / 2计算即可。
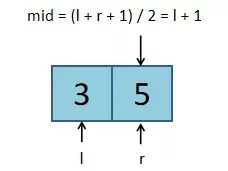
等等,这样会出引入一个新的问题
mid的值通过(l + r + 1) / 2 计算。在区间内只有两个元素的时,l的值可以用r - 1代替。因此mid = (l + r) / 2 = (r - 1 + r + 1) / 2 = r。
如果程序用r = mid更新右边界,更新后r = r,区间不变,陷入死循环。
所以,当程序中r的更新为r = mid 时,mid的值计算不能用 (l + r + 1) / 2。
总结:
mid 用(l + r) / 2计算时,如果程序中有l = mid ,程序会陷入死循环。
mid 用(l + r + 1) / 2计算时,如果程序中有r = mid ,程序会陷入死循环。
如何优雅的解决左右端点更新的问题
-
程序中不要同时出现l = mid, r = mid这两条语句。
-
如果程序中出现了l = mid,mid的值用 (l + r + 1) / 2计算。
-
如果程序中出现了r = mid,mid的值用((l + r) / 2计算。
模板如下:
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + (r - l >> 1);// r用mid更新,mid用l + r >> 1计算
if (check(mid)) r = mid; // r用mid更新,mid用l + r >> 1计算
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + (r - l + 1 >> 1);
if (check(mid)) l = mid;//l用mid更新,mid用l + r + 1 >> 1计算
else r = mid - 1;//l用mid更新,mid用l + r + 1 >> 1计算
}
return l;
}
2.2 何时停止二分
每次二分,通过更新l或r不断缩小区间,并保证答案一定在区间内。当区间内只有一个元素时,判断这个元素是否为答案,完成算法。
优雅的停止二分:
当l<r成立时,进行二分。l = r时停止。停止后进行判断,是答案输出,不是答案,此题无解。
模板如下:
int l = 0, r = n;//n为初始时区间右端点,
while (l < r) {//l< r进行二分,l = r的时停止二分
int mid = 中间点;
if (更新r的条件成立)
更新r;
else
更新l;
}
//循环结束时,[l,r]区间内只有一个元素
if (区间内元素是答案)
输出答案;
else
答案不存在;
我们写出这一章开始例子的代码:
int findLast(vector<int> a, int t) {
int l = 0, r = a.size();
while (l < r) {//l<r进行二分,直到l=r时,停止二分
int mid = l + (r - l + 1)/ 2;//下方语句,出现了l = mid,mid要用(l + r + 1) / 2计算
if (a[mid] > t)//a[mid] > t,t最后一次出现的位置一定在mdi之前
r = mid - 1;
else //a[mid] <= t,t最后一次出现的位置一定在mdi处或者mid之后
l = mid;//出现了l = mid,mid要用(l + r + 1) / 2计算
}
//因为答案存在,并且二分过程中保证了答案一直在区间[l,r]中,当[l,r]中只有一个元素时,即为答案。
return l;
}
如果题目改成求target第一次出现的位置,程序如下:
int findFirst(vector<int> a, int t) {
int l = 0, r = a.size();
while (l < r) {
int mid = l + (r - l) / 2;//下方语句,出现了r = mid,mid要用(l + r ) / 2计算
if (a[mid] >= t)//a[mid] >= t,t第一次出现的位置一定在mdi或者mid之前
r = mid;
else //a[mid] < t,t第一次出现的位置一定在mid之后
l = mid + 1;//出现了r = mid,mid要用(l + r) / 2计算
}
//因为答案存在,并且二分过程中保证了答案一直在区间[l,r]中,当[l,r]中只有一个元素时,即为答案。
return l;
}
NO.3 二分法一定要有序才能使用吗?
3.1 先看一个例子
设想另一个猜数字游戏:小明写下一个包含10个无序数字的序列,让小刚猜其中一个数字的位置。小刚每猜一次位置,小明会给提醒:目标在猜的位置左侧还是右侧。
依旧可以用二分法快速找到目标的位置。
例如:小明写下的序列为:[15,12,18,13,17,14,19,16,11,10],要猜出19所在的位置。序列一共10个元素,分布在从0到9的位置。小刚可以这样猜:
第一次猜0–9的中间位置:(0 + 9) / 2 = 4。小明给出提醒:19在位置4的右侧。
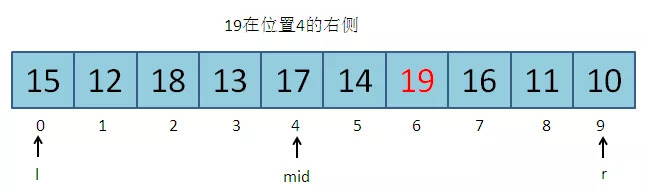
第二次猜5–9的中间位置:(5 + 9) / 2 = 7。小明给出提醒:19在位置7的左侧。

第三次猜5–7的中间位置:(5 + 7) / 2 = 6。19在位置6,游戏结束。
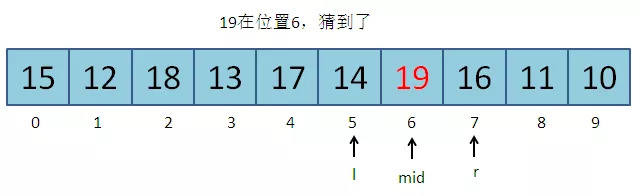
猜数字过程中,只要能判断答案在猜的位置左边还是右边,就能更新区间。
3.2 使用二分法的关键
是否可以使用二分法的关键在于:二分后,能否判断出答案所在的区间,而不是数据是否有序。
同理,找数字最后一次出现位置的例子中,可以使用二分法原因是:每次二分后,能通过中间值与目标值的大小关系判断出答案所在区间。关键点在于:二分后能判断出答案所在区间。
如果数据无序,能通过其他方法确定答案所在区间,同样也可以使用二分法。
3.3 一道题
给定一个整数的数组,每个元素都出现了两次,并且相同元素相邻,唯有一个元素出现了一次,找出这个数字。
例如:数组a:为[3,3,8,8,9,1,1]。因为9只出现了一次,所以输出9。
数组是无序的,能不能使用二分法呢?关键在于二分后能判断出答案所在区间。
思考:
-
数组中只有一个元素出现了一次,其他元素出现次2次。所以数组的元素个数一定为奇数个。
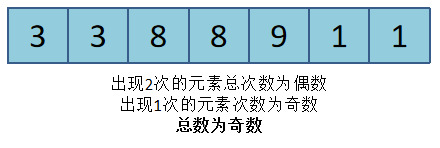
-
用mid指向中间数字,如果这个数字出现了两次,把这对数字去掉,数组会被分成左右两部分,一部分元素个数为奇数,另一部分元素个数为偶数。
出现了一次的数字,要么在左侧数组,要么在右侧数组。
包含出现一次数字的数组,元素个数为奇数个;不包含出现一次数字的数组,元素个数为偶数个。

- 如果mid指向的数字只出现了一次,这个数字就是答案。
思考2可以得出:二分后,答案在元素个数为奇数的那个数组中。所以可以使用二分法,代码如下。
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
if(nums.size() == 1) return nums[0];//特殊情况先处理
int l = 0, r = nums.size() - 1;
while(l < r){
int mid = l + (r - l >> 1);// >> 1,等价于除以2。
if(nums[mid] == nums[mid + 1]){// a[mid]和后一个元素相等
if((r - (mid + 1)) % 2 == 1) l = mid + 2;//右边有奇数个元素,答案在右边,更新l
else r = mid - 1;//左边有奇数个元素,答案在左边,更新r
}
else if(nums[mid] == nums[mid -1]){// a[mid]和前一个元素相等
if((r - mid) % 2 == 1) l = mid + 1;//右边有奇数个元素,答案在右边,更新l
else r = mid - 2;//左边有奇数个元素,答案在左边,更新r
}
else
return nums[mid];//a[mid]与前一个后一个元素都不等,该元素就是答案
}
return nums[l];//只剩一个元素,就是答案。
}
};
NO.4 证明二分法的时间复杂度
二分法每次区间长度缩小为原来的二分之一。当区间内只有一个元素时停止。
设开始时数组中元素个数为n。
-
第一次二分后:答案所在区间长度缩小一半:n / 2。
-
第二次二分后:答案所在区间长度缩小一半:n / 4。
-
第k次二分后:答案所在区间长度缩小一半:n / 2^k。
-
第logn次二分后:答案所在区间长度缩小一半:n / 2^long = 1,停止二分。
总共处理了logn次,每次处理的时间复杂度是O(1)。所以总时间复杂是O(logn)。
NO.5 一些题目
Leetcode:
658.找到K个最接近的元素
911.在线选举
718.最长重复子数组
378.有序矩阵中第K小的元素
497.非重叠矩形中的随机点
475.供暖器
167.两数之和II—输入有序数组
287.寻找重复数
704.二分查找
209.长度最小的子数组
69.x的平方根
162.寻找峰值
981.基于时间的键值存储
50.Pow(x,n)
436.寻找右区间
349.两个数组的交集
350.两个数组的交集II
528.按权重随机选择
392.判断子序列
29.两数相除
374.猜数字大小
275.H指数II
278.第一个错误的版本
367.有效的完全平方数
441.排列硬币
35.搜索插入位置
744.寻找比目标字母大的最小字母
852.山脉数组的峰顶索引
转载于公众号 猿六学算法


66666666666666666666
呜呼
可以
可以
可以