裴蜀定理

裴蜀定理是一个关于最大公约数的定理。若$a,b$是整数，且$\gcd(a,b)=d$，那么对于任意的整数$x,y$，$ax+by$都一定是$d$的倍数，特别地，一定存在整数$x,y$，使$ax+by=d$成立。它的一个重要推论是：$a,b$互质的充要条件是存在整数$x,y$使$ax+by=1$。

裴蜀定理的证明方法有很多种，以下是其中一种常见的证明方法：

已知$a,b$是整数，且$\gcd(a,b)=d$，则可设$a=md$，$b=nd$，其中$m,n$是整数。

对于任意的整数$x,y$，有$ax+by=mdx+ndy=d(mx+ny)$，因为$mx+ny$是整数，所以$ax+by$是$d$的倍数。

特别地，当$x=1$，$y=-1$时，$ax+by=md-n= d(m-n)$。因为$m-n$是整数，所以存在整数$x,y$，使$ax+by=d$成立。

反之，若存在整数$x,y$使$ax+by=d$成立，则$d$是$ax+by$的因数，又因为$d$是$a,b$的最大公约数，所以$d$是$a,b$的公因数，即$a,b$互质。

因此，裴蜀定理成立。

扩展欧几里得算法

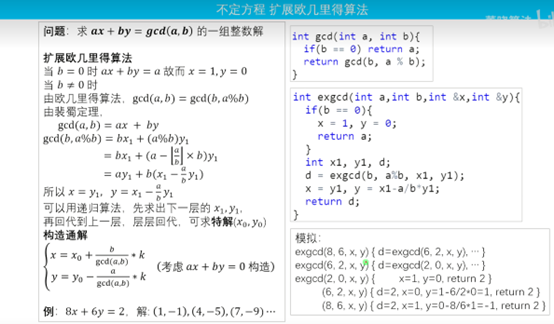
以上内容取自：【G17 不定方程 扩展欧几里得算法】https://www.bilibili.com/video/BV1rD4y1C7qg?vd_source=5b08a235ad6a90b6c35af25ededc9fd4