图论–最短路问题

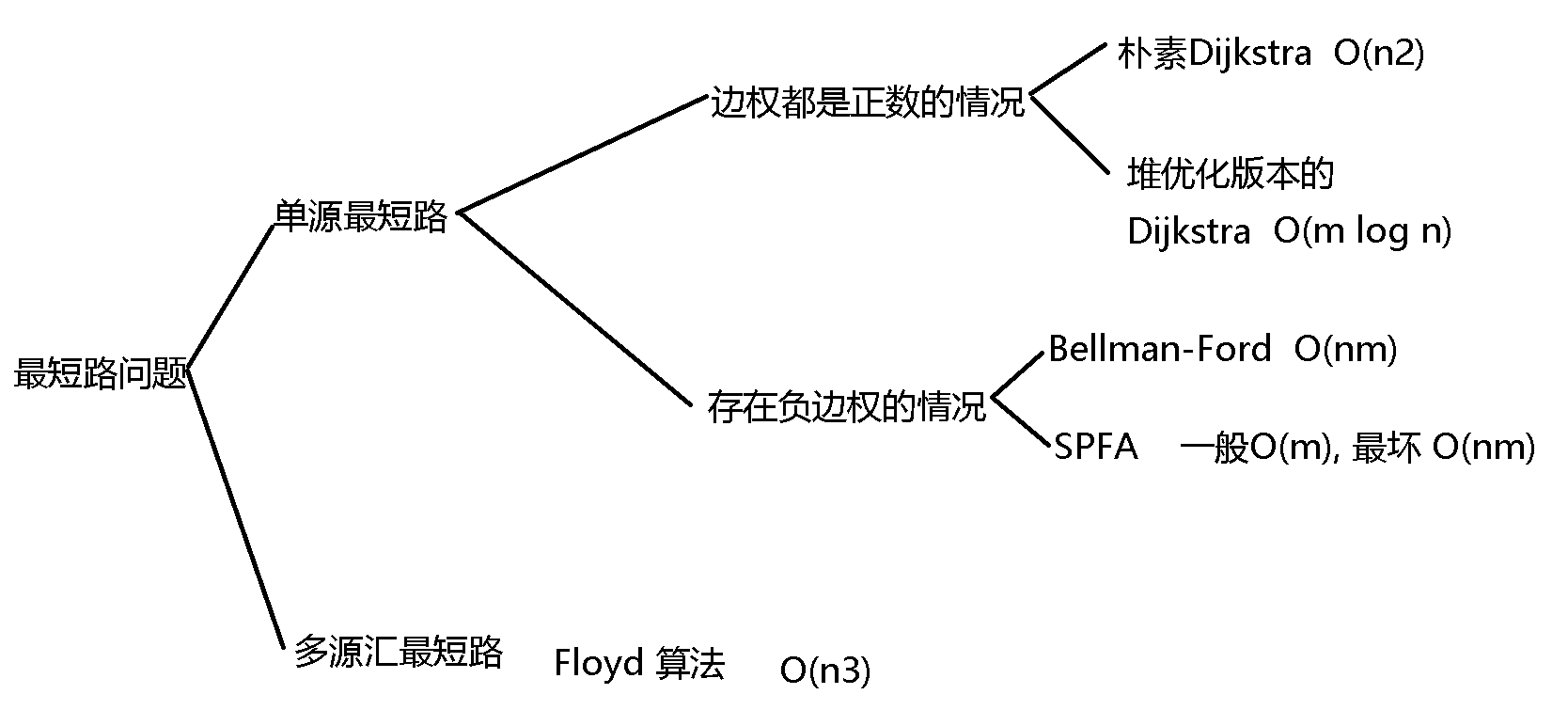
其中求最短路常用的算法有上面几种， 根据题目给出的相关限制条件来选选择对应的算法，例如Dijkstra算法是不能处理负边权的情况，朴素版本Dijkstra和堆优化版本的Dijkstra，并不是朴素版就比优化版差，当图为稠密图时偏向于使用朴素版本的，因为当 m > n2 时，此时堆优化版本相比朴素版本时间复杂度高。计算存在负边权时的两种算法，spfa是对bellman—ford算法的改进，但bellman-ford代码实现比较简单。对于多源汇合最短路，这里只有一个Floyd算法，其算法原理基于dp。下面具体讲解一下上面的算法，及其代码实现.

Dijkstra算法

这个算法的讲解之前我就写过，所以直接从下面的链接进入就可以看到.
Dijkstra算法讲解

Bellman-Ford 算法

上面分析Dijkstra算法的时候，解释了为什么存在负权边的情况下不能用Dijkstra算法， 因为Dijkstra每次从堆顶取出的点都是距离起点最近的点，是基于贪心实现的，若存在负边权，虽然从堆顶出的点是距离起点最近的，但可能存在一条路径此时某个节点距离起点距离过大，只能在后面弹出，但该路径存在负权边，故这就造成了这个节点只能在其他节点遍历完毕之后再出堆，但此时这条路径已经不能继续遍历了，因为有的节点已经给标记为遍历状态，带来的结果就是，Dijkstra算法无法再确定从起点到这一点的最小距离，因为总可能有像这样未被遍历的点存在。故bellman_ford算法相比于Dijkstra算法就是没有了标记数组，直接每次都遍历所有的边，一直更新,即可重复遍历某个节点。

例题 ： 853. 有边数限制的最短路

代码实现

#include<iostream>
#include<cstring>
using namespace std;

constexpr int N = 1e+6, INF = 0x3f3f3f3f;
int n, m,k, d[N], temp[N];

struct 
{
    int a, b, w;  // 直接存储每条边的信息便于遍历，因为全部都要遍历一遍，故这里直接结构体比邻接表方便
}edge[N];

auto bellman_ford()
{
    d[1] = 0;
    for(int i = 1; i <= k; ++i)   // 遍历k次的含义是计算出不超过k条边情况下的某个节点距离起点的最短距离
    {
        // 解释一下上面那句话，因为遍历一次是遍历一条边的, 例如边 a->b ,长度为m, 则d[b]会判断是否进行更新
        // 若进行更新是用上次更新的结果来的，故这里用temp数组保存一下上次的d数组的结果
        memcpy(temp, d, sizeof d); 
        for(int j = 1; j <= m; ++j) // 每次都遍历一遍所有边，即相比Dijkstra算法重复遍历某个节点
        {
            auto e = edge[j];
            d[e.b] = min(d[e.b], temp[e.a] + e.w);     // 更新
        }
    }
    if(d[n] > INF / 2) cout << "impossible" << endl;  // 由于存在负权边，故条件是 > INF , 而不能写成 == INF 
    else cout << d[n] << endl;
}

auto main() -> int
{
    memset(d, 0x3f, sizeof d);
    cin >> n >> m >> k;
    for(int i = 1;i <= m; ++i)
    {
        int a, b, c; cin >> a >> b >> c;
        edge[i] = {a, b, c};
    }
    bellman_ford();
}

SPFA 算法

SPFA算法是对bellman_ford算法的改进， 我们观察bellman_ford算法可以改进的地方，首先为了解决Dijkstra可能漏掉某些节点的重新遍历，bellman_ford算法的解决方式，每次都是遍历一遍所有边，即这个操作

        for(int j = 1; j <= m; ++j) 
        {
            auto e = edge[j];
            d[e.b] = min(d[e.b], temp[e.a] + e.w);     // 更新
        }
// 可以看出要想d[e.b]发生更新，必须d[e.a] 发生变化，因为d[e.b] 和 e.w 这两项是不变的
// 故我们改进的思路就是当某个节点的距离重新更新之后，才遍历其连接的下一节点
// 故为了便于找到其某个节点连接的下一节点，这里最好的方式还是邻接表的实现

代码实现

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

constexpr int N = 1e+5 + 10, INF = 0x3f3f3f3f;
int n, m, g[N], d[N], e[N], ne[N], idx, w[N];    // 为了便于找到其连接的下一节点这里采用邻接表
bool st[N];

auto add(int a, int b, int c)
{
    e[idx] = b, ne[idx] = g[a], w[idx] = c, g[a] = idx++; 
}

auto spfa() 
{
    queue<int> q;     // 保存进行遍历的节点，这里其实用什么容器都行
    d[1] = 0;         // 初始化起点
    q.push(1);        
    st[1] = true;     // st数组并不是标记是否被遍历，而是标记是否在队列中等待遍历，减少无效操作次数
    while(q.size())
    {
        int node = q.front(); q.pop();
        st[node] = false;
        for(int i = g[node]; i != -1; i = ne[i])
        {
            int t = e[i];
            if(d[t] > d[node] + w[i])  // 若其到起点的距离发生更新，则将其入队表示下次更新其连接的下一节点
            {
                d[t] = d[node] + w[i];
                if(!st[t]) q.push(t), st[t] = true;
            }
        }
    }
    if(d[n] > INF / 2) cout << "impossible" << endl;
    else cout << d[n] << endl;
}

auto main() -> int
{
    memset(g, -1, sizeof g);
    memset(d, 0x3f, sizeof d);
    cin >> n >> m;
    while(m--)
    {
        int a,b,c; cin >> a >> b >> c;
        add(a, b, c);
    }
    spfa();
    return 0;
}

Floyd 算法

这针对多源最短路的问题， 即此时求解的答案并不是计算从1号节点到n号节点的最短距离，是计算从任意节点到另外一个节点的最短距离， 这个算法的思路是基于DP的, 故这里采用闫氏dp分析法分析一波

闫氏dp分析法

                             | 集合: 从i这个点开始，到达j的路径集合
                             |
  |------------状态表示 -----|
  |             f(i,j)       | 属性 : 集合中可行方案路径最短的值 min
  | 
  | 
  |
  DP    
  |
  |
  |
  |
  |------------状态计算 : 根据集合划分，将一个大集合划分为若干个子集， 
                          设我们要求解f(i,j), 然后来尝试将其分为更小的集合

将 f(k, i, j) 分解为两为两部分

由题意可以知道， 任意节点 i –> j 的最短路径有两种途径
(1) 直接从i –> j
(2) 从i经过若干个节点后到达一个节点k, 再由k到j;

f(i,j) 表示的含义就是节点 i 到 j 的最短路径的距离, 对于任意节点k, 判断是否存在f(i,k) + f(k,j) < f(i,j), 若存在则用它更新f(i,j);

#include<iostream>
using namespace std;
constexpr int N  = 210, INF = 0x3f3f3f3f;
int n, m, k, f[N][N];

auto floyd()
{
    for(int k = 1; k <= n; ++k)
        for(int i = 1; i <= n; ++i)
            for(int j = 1; j <= n; ++j)
                f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}

auto main() -> int
{
    cin >> n >> m >> k;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= n; ++j)
            if(i == j) f[i][j] = 0;
            else f[i][j] = INF;
    while(m--)
    {
        int a, b, c; cin >> a >> b >> c;
        f[a][b] = min(f[a][b], c);
    }
    floyd();
    while(k--)
    {
        int a, b; cin >> a >> b;
        if(f[a][b] > INF / 2) cout << "impossible" << endl;
        else cout << f[a][b] << endl;
    }
    return 0;
}