二分图

  |------------染色法 O(n2)
  |                          
  | 
  | 
  |
  二分图相关算法    
  |
  |
  |
  |
  |----------- 匈牙利算法 (最坏O(mn), 但实际运行效果较好，远小于mn)

首先搞清楚二分图的概念，简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。

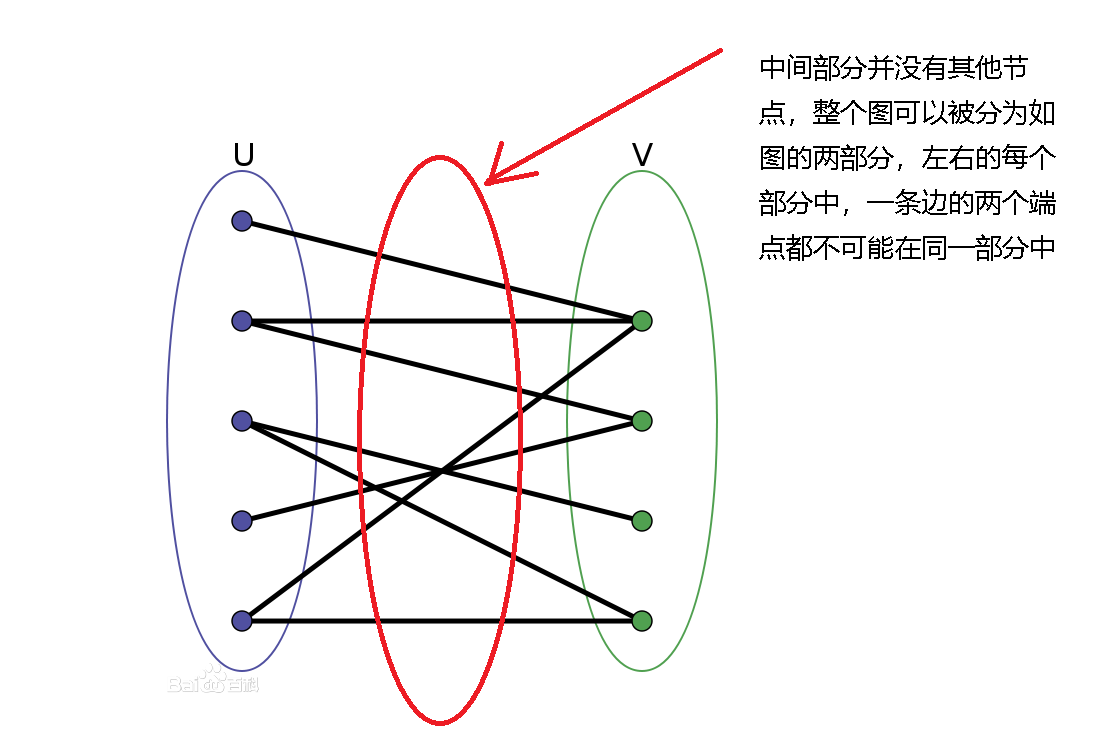
二分图中的一个重要性质: 若一个图中存在奇数环(即存在节点数为奇数个的环)，则该图不可能是二分图。 因为根据二分图的定义，若要保证两个集合的中间不存在节点，故每一条边的两个端点必定是不同的部分，若存在奇数环，则从任意一个点开始，标记为1，表示左半部分，然后其连接的下一节点必定为右部分，标记为2，依次类推再下一个标记为1，若为奇数环，则就会出现矛盾的情况。

染色法

其实就是上面分析性质的过程，遍历所有的节点,然后遍历其连接的下一节点，依次标记为不同的颜色，这里的话在算法实现上dfs和bfs都是可以的，若在这个过程中出现矛盾的情况则表示该图不为二分图.

练习链接: 860. 染色法判定二分图
代码实现

#include<iostream>
#include<cstring>
using namespace std;

constexpr int N = 2e+5 + 10;

int n,m,g[N], e[N], ne[N], idx; // 为了方便遍历一个节点所相连的其他节点，这里采用邻接表储存
int color[N];

auto add(int a, int b)
{
    e[idx] = b, ne[idx] = g[a], g[a] = idx++;
}


auto dfs(int u, int c) -> bool    // 这里采用dfs遍历每个节点及其所相连的节点
{
    color[u] = c;
    for(int i = g[u]; i != -1; i = ne[i])   // 依次遍历u节点所相连的其他节点    
    {
        int t = e[i]; 
        if(!color[t])             // 若该节点为被染色, 则进行染色, 1, 2代表两种颜色
        {
            if(!dfs(t, 3 - c)) return false;   // 3 - c 表示染上和c不同的颜色
        }
        else if(color[t] == c) return false;   // 若该节点未被染色并且和上一节点颜色相同则矛盾
    }
    return true;
}

auto main() -> int
{
    memset(g, -1, sizeof g);
    cin >> n >> m;
    while(m--)
    {
        int a, b; cin >> a >> b;
        add(a, b), add(b,a);
    }
    for(int i = 1; i <= n; ++i)   // 依次遍历每一个节点
    {
        if(!color[i])
        {
            if(!dfs(i, 1))        // 若出现冒充直接goto到end结束
            { 
                cout << "No" << endl;
                goto end;
            }
        }
    }
    cout << "Yes" << endl; 
end:
    return 0;
}

匈牙利算法

匈牙利算法主要解决二分图中的最大匹配问题，首先来了解一下什么叫二分图的匹配, 给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

如左图所示的是一个二分图，可以分为左部分集合为 u, 右半部分集合为v, 然后根据匹配的定义，任意两条边都不依附于同一个顶点。我们可以看到左图的5号顶点中，有三条边依附于5号节点上， 2条边依附于7号节点上。 故这些边并不能算作是一种匹配的情况，故在右图的情况中属于图的一个边集， 即符合匹配的条件，且最大匹配数即为为4条边，故结果为4.

故匈牙利算法的思路: 模拟一下算法的过程， 首先从原本的二分图中，我们看作是遍历作半部分的节点，然后找到唯一一个与其匹配的右边节点，例如从左图中1号节点可以匹配5号节点和7号节点，故先让其匹配5号节点，此时算作一个匹配，然后遍历左边的下一节点2，此时它只能与5号点匹配，但是5号节点已经和1号点匹配，此时再考虑1号点有没有其他匹配的方案，发现1号点可以和7号匹配，故1号重新和7号匹配，2号和5号匹配， 故此时已经有两个匹配，然后继续遍历左边剩余节点，此时遍历3号节点，3号节与5号节点和6号节点相连，我们从上到下的顺序依次判断，首先是5号节点，此时5号节点已经和2号节点匹配，然后回去判断2号节点是否能和其他节点匹配，发现没有其他节点符合条件，故此时再判断6号节点，发现还没有其他节点与其匹配，故匹配成功。继续遍历左边的剩余节点。此时剩下4号节点，与其相连的节点有7号节点和8号节点，首先判断是否能和7号节点匹配，发现7号节点已经和1号节点匹配，故看看1号节点能不能和其他节点匹配，发现其能和5号节点匹配，但5号节点已经和2号节点匹配，故再看看2号节点能不能换一个匹配，发现不行。故4号点此时不能和7号点匹配，故判断一下能否和8号点匹配，发现8号点还没有匹配，故成功匹配上。 故左边所有节点匹配完毕，匹配数为4；

分析完过程，看看代码实现
练习链接 ： 861. 二分图的最大匹配

#include<iostream>
#include<cstring>
using namespace std;
constexpr int N = 1e+5 + 10;
int n1, n2, m, e[N], ne[N], idx, g[N];// 为了便于找出节点相连的节点，采用邻接表的方式更方便
int match[N];// 用于标记右半部分的节点匹配的是左半部分那个节点    
bool st[N];  // 用于表示那个节点已经处于尝试匹配当中，或者就是表示该节点准备被匹配，其他已匹配到的节点另寻其他节点

auto add(int a, int b)
{
    e[idx] = b, ne[idx] = g[a], g[a] = idx++;   
}

auto find(int x) -> bool    // 寻找未被匹配的节点
{
    for(int i = g[x]; i != -1; i = ne[i])  // 依次遍历与自身节点相连的其他节点
    {
        int t = e[i];               
        if(st[t]) continue;    // 若该节点已被其他节点尝试匹配，则尝试下一节点
        st[t] = true;          // 标记右边的t节点为尝试匹配状态
        if(!match[t] || find(match[t]))  // 若此时右边的t节点未被匹配, 或者左边匹配到t的节点能换成另外一个节点则匹配成功
        {
            match[t] = x;      // 更新右边的t节点匹配左边的x节点
            return true;
        }
    }
    return false;
}

auto main() -> int
{
    cin >> n1 >> n2 >> m;
    memset(g, -1, sizeof g);
    while(m--)
    {
        int a, b; cin >> a >> b;
        add(a, b);
    }
    int res = 0;
    for(int i = 1; i <= n1; ++i)
    {
        memset(st, false, sizeof st);
        if(find(i)) res++;      // 匹配成功依次，则匹配数++
    } 
    cout << res << endl;

}